Классификация случайных процессов

Как я уже говорил ранее число возможных состояний (пространство состояний) случайного процесса может быть конечным или бесконечным поэтому можно привести следующую классификацию случайных процессов:

· дискретное время, дискретное состояние,

· непрерывное время, дискретное состояние,

· дискретное время, непрерывное состояние,

· непрерывное время, непрерывное состояние.

Случайный процесс X(t) называется процессом дискретным во времени, если система в которой он протекает, меняет свои состояния только в моменты времени t₁, t₂,…,t_n, число которых конечно или счетно.

Случайный процесс называется процессом с непрерывным временем, если переход их состояния в состояние может происходить в любой момент времени.

Случайный процесс называется процессом с непрерывными состояниями, если значением случайного процесса является непрерывная случайная величина.

Случайный процесс называется случайным процессом с дискретными состояниями, если значением случайного процесса является дискретная величина.

Виды случайных процессов:

· нестационарные,

· стационарные,

· эргодические.

Наиболее общий случайный процесс – нестационарный.

Случайный процесс называется нестационарным, если его вероятностные характеристики зависят (изменяются) от времени.

Нестационарные случайные процессы нельзя исследовать по одной реализации, как бы продолжительна она ни была.

Унестационарных случайных процессов вид корреляционной функции зависит от рассматриваемого момента времени и она должна определяться по ансамблю реализацией.

Характеристикинестационарных случайных процессов представляют собой функции времени, которые можно определить только усреднением мгновенных значений процессов по множеству реализаций.

Случайный процесс называется стационарным, если все многомерные законы распределения зависят только от взаимного расположения моментов времени , но не от самих значений этих величин.

Другими словами, случайный процесс называется стационарным, если его вероятностные закономерности неизменны во времени.

Для стационарного случайного процесса X(t) его многомерная плотность вероятности зависит только от величины интервалов 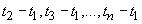и не зависит от положения этих интервалов в области изменения аргумента t₁.

Отсюда следует, что

во-первых, для стационарного процесса одномерная плотность вероятности не зависит от времени, т.е. ;

во-вторых, двумерная плотность вероятности зависит от разности , т.е. и т.д. В связи с этим все моменты одномерного распределения, в том числе математическое ожидание и дисперсия, постоянны.

Стационарный случайный процесс называется эргодическим, если при определении любых статистических характеристик усреднение по множеству реализаций эквивалентно усреднению по времени одной бесконечно длинной реализации.

Эргодичность является очень важным свойством случайных стационарных, и только стационарных процессов. Математическое ожидание эргодического случайного процесса равно постоянной составляющей любой его реализации, а дисперсия является мощностью его флюктуационной составляющей. Так как определение функций производится по ограниченным статистическим данным одной реализации и является только определенным приближением к соответствующим фактическим функциям процессов, целесообразно называть эти функции статистическими.

Случайный процесс описывается статистическими характеристиками, называемыми моментами.

В практике анализа случайных процессов используются, в основном, начальные моменты первого порядка и центральные моменты второго порядка.

Математическое ожидание (mean, value) является первым начальным моментом случайного процесса и представляет собой статистическое усреднение случайной величины X(t_i) в каком либо фиксированном сечении t_i случайного процесса. Соответственно, полная функция математического ожидания является теоретической оценкой среднего взвешенного значения случайного процесса по временной оси:

m_x(t) º M{Х(t)}º 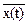= 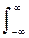x p(x; t) dx

Математическое ожидание m_x(t) представляет собой неслучайную составляющую случайного процесса X(t).

Второй начальный момент случайного процесса определяет его среднюю мощность:

w_x(t) º M{Х²(t)}º 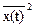= 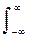x² p(x; t) dx

Функция дисперсии (variance, function of a dispersion) случайного процесса. При анализе случайных процессов особый интерес представляет флуктуационная составляющая процесса, которая определяется разностью Х(t)-m_x(t). Функция дисперсии является теоретической оценкой среднего взвешенного значения разности Х(t)-m_x(t)², т.е. является вторым центральным моментом процесса, и определяет мощность его флуктуационной составляющей:

D_x(t) = M{[Х(t)-m_x(t)]²} = M{X²(t)} - m_x²(t) = 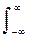[x_o(t)]² p(x; t) dx,

где x_o(t) = x(t)-m_x(t).

Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса значений случайного процесса по временной оси относительно математического ожидания процесса:

σ_x(t) = .

Дисперсия случайной величины обычно обозначается индексом σ².

Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.

Двумерная плотность распределения вероятностей p(x₁,t₁; x₂,t₂) определяет вероятность совместной реализации значений случайных величин Х(t₁) и Х(t₂) в произвольные моменты времени t₁ и t₂, что характеризует взаимосвязь случайного процесса в различные моменты времени и дает возможность определить характер изменения случайного процесса, т.е. динамику развития процесса во времени. Распределение описывает двумерную случайную величину {X(t_i), X(t_j)} в виде функции вероятности реализации случайной величины X(t_i) в бесконечно малом интервале dx_i в окрестностях x_i в момент времени t_i при условии, что в момент времени t_j значение X(t_j) будет реализовано в бесконечно малом интервале dx_j в окрестностях x_j:

p(x₁,t₁; x₂,t₂) = P{x₁ ≤ x(t₁) ≤ x₁+dx₁ Ç x₂ ≤ x(t₂) ≤ x₂+dx₂ }.

С помощью двумерной плотности распределения вероятностей можно определить корреляционные функции процесса.

Корреляционные функции случайных процессов. Характеристикой динамики изменения случайной величины X(t_i) является корреляционная функция, которая описывает случайный процесс в целом:

R_X(t_i, t_j) = M{X(t₁) X(t₂)}.

Корреляционная функция представляет собой статистически усредненное произведение значений случайного процесса X(t) в моменты времени t_i и t_j по всем значениям временных осей t_i и t_j, а, следовательно, тоже является двумерной функцией. В терминах теории вероятностей корреляционная функция является вторым начальным моментом случайного процесса.

Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t₁ и t₂ и производится функцией корреляции. По всему пространству значений случайного процесса X(t) корреляционная функция определяется выражением:

R_X(t_i, t_j) = 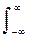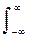x(t_i)x(t_j) p(x_i,t_j; x_i,t_j) dx_i dx_j,

При анализе случайных процессов второй момент времени t_j удобно задавать величиной сдвига τ относительно первого момента, который при этом может быть задан в виде координатной переменной:

R_X(t, t+ τ) = M{Х(t)Х(t+ τ)}.

Функция, задаваемая этим выражением, обычно называется автокорреляционной функцией случайного процесса.

Ковариационные функции. Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m_x(t) в моменты времени t_i и t_j и характеризует флюктуационную составляющую процесса:

K_Х(t_i, t_j) = 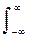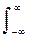(x(t_i)-m_x(t_i)) (x(t_j)-m_x(t_j)) p(x_i,t_j; x_i,t_j) dx_i dx_j,

В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции автокорреляции. При произвольных значениях m_x ковариационные и корреляционные функции связаны соотношением:

K_X(t, t+ τ) = R_X(t, t+ τ) - m_x²(t).

Нормированная функция автоковариации (функция корреляционных коэффициентов):

r_Х(t,t+ τ) = K_X(t,t+ τ)/[ σ (t) σ (t+ τ)].

Функция корреляционных коэффициентов может принимать значения от +1 (полная статистическая корреляция случайных процессов на интервалах t и t+ τ) до -1 (полная статистическая противоположность процессов на этих интервалах). Попутно отметим, что в математической статистике, а также довольно часто и в технической литературе, эту функцию называют функцией корреляции. При τ=0 значение r_Х равно 1, а ФАК вырождается в дисперсию случайного процесса:

K_X(t) = D_X(t).

Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и корреляции (ковариации). Особой необходимости в отдельной функции дисперсии не имеется.