Предположим для простоты, что ячейка кристалла имеет форму прямоугольного параллелепипеда. Длины ребер  .
. 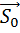 - единичный вектор падающей волны.
- единичный вектор падающей волны.
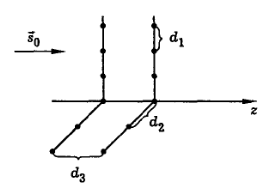
Определим направление на главные максимумы. Кристаллическую решетку можно рассматривать как последовательность двухмерных плоских решеток, отстоящих друг от друга на расстояние 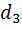 . Направление на главные максимумы дифракционной картины, возникающей при дифракции волны на отдельной двумерной решетке, определяются предыдущими формулами. Однако, выполнение этих условий еще не дает гарантии того, что в двух направлениях
. Направление на главные максимумы дифракционной картины, возникающей при дифракции волны на отдельной двумерной решетке, определяются предыдущими формулами. Однако, выполнение этих условий еще не дает гарантии того, что в двух направлениях 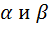 будут возникать дифракционные максимумы. Это зависит от того, как будут интерферировать между собой волны, дифрагировавшие на разных атомных плоскостях.
будут возникать дифракционные максимумы. Это зависит от того, как будут интерферировать между собой волны, дифрагировавшие на разных атомных плоскостях.
Условие интерференционного усиления волн, идущих от двух соседних атомных плоскостей, имеет вид:
 ,
,
где  – целое число. Формула выражает требование того, чтобы разность хода лучей от двух соседних атомных плоскостей в направлении
– целое число. Формула выражает требование того, чтобы разность хода лучей от двух соседних атомных плоскостей в направлении 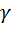 была кратна длине волны. В этом случае волны, дифрагировавшие на разных атомных плоскостях, будут складываться, в противном случае они гасятся, т. е. полная система уравнений:
была кратна длине волны. В этом случае волны, дифрагировавшие на разных атомных плоскостях, будут складываться, в противном случае они гасятся, т. е. полная система уравнений:


- уравнение Лауэ для случая, когда волна распространяется вдоль оси 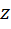 , перпендикулярной атомным плоскостям. Для произвольного падения (
, перпендикулярной атомным плоскостям. Для произвольного падения (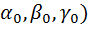

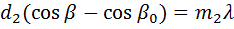


Система уравнений имеет решения лишь для некоторых определенных значений длины волны излучения  или определенных углов
или определенных углов  , определяющих ориентацию кристалла относительно падающей волны. Поэтому для получения дифракционных картин на практике используют рентгеновское излучение с широким частотным спектром, либо вращают кристалл относительно монохроматического пучка рентгеновского излучения с помощью специального гониометрического устройства.
, определяющих ориентацию кристалла относительно падающей волны. Поэтому для получения дифракционных картин на практике используют рентгеновское излучение с широким частотным спектром, либо вращают кристалл относительно монохроматического пучка рентгеновского излучения с помощью специального гониометрического устройства.
Рентгеновский структурный анализ.
Применительно к дифракции рентгеновских лучей в кристаллах большое значение имеет решение обратной задачи дифракции: определение структуры кристалла по виду наблюдаемой дифракционной картины. Получение такой информации составляет предмет рентгеновского структурного анализа.
В основе рентгеноструктурного анализа лежат формулы, описывающие фраунгоферову дифракцию на трехмерной структуре.

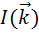 - распределение интенсивности излучения в дифракционной картине,
- распределение интенсивности излучения в дифракционной картине, 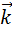 - вектор, направленный от объекта в точку наблюдения.
- вектор, направленный от объекта в точку наблюдения.
 (1)
(1)
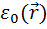 – исходное распределение поля в пространстве, определяется структурой объекта, на котором дифрагирует рентгеновская волна, а именно пространственным распределением плотности
– исходное распределение поля в пространстве, определяется структурой объекта, на котором дифрагирует рентгеновская волна, а именно пространственным распределением плотности  в кристалле:
в кристалле:  . Обращая формулу (1), получаем:
. Обращая формулу (1), получаем:
 (2)
(2)
Таким образом, формула (1) описывает Фурье-анализ электронной плотности в кристаллах, выполняемый автоматически в рентгенодифракционном эксперименте, а формула (2) описывает Фурье-синтез структуры кристалла, которой может быть выполнен численно на ЭВМ. В настоящее время рентгеноструктурный анализ представляет собой хорошо разработанную методику, с помощью которой определено строение многих минералов и сложных молекул, включая биологические (ДНК, гемоглобин).
Итак, реальные возможности спектрального прибора определяются шириной и формой его аппаратной функции (инструментального контура). Возможность разделить две монохроматические линии зависит от точности, с которой измерена аппаратная функция и может быть измерена наблюдаемая функция. Поэтому количественный критерий может быть сформулирован только условно в предположении определенной точности измерений интенсивности. Условный критерий был предложен Релеем. Согласно критерию Релея наименьший разрешимый интервал  равен расстоянию между главным максимумом и ближайшим к нему минимумом аппаратной функции. Две монохроматические линии одинаковой интенсивности на таком расстоянии друг от друга (в угловой мере
равен расстоянию между главным максимумом и ближайшим к нему минимумом аппаратной функции. Две монохроматические линии одинаковой интенсивности на таком расстоянии друг от друга (в угловой мере  ) дают суммарный контур с двумя максимумами, провал между которыми составляет около 20 % от интенсивности в максимумах. Благодаря провалу такой контур воспринимается как двойная спектральная линия. Если считать критерием разрешения именно наличие провала, то можно обобщить критерий Релея на случай, когда аппаратная функция отличается от дифракционной. При любой форме инструментального контура две монохроматические линии одинаковой интенсивности находятся на пределе разрешения
) дают суммарный контур с двумя максимумами, провал между которыми составляет около 20 % от интенсивности в максимумах. Благодаря провалу такой контур воспринимается как двойная спектральная линия. Если считать критерием разрешения именно наличие провала, то можно обобщить критерий Релея на случай, когда аппаратная функция отличается от дифракционной. При любой форме инструментального контура две монохроматические линии одинаковой интенсивности находятся на пределе разрешения  , если провал в суммарном конуре составляет 20 %.
, если провал в суммарном конуре составляет 20 %.
Рисунок
Необходимо подчеркнуть условный характер критерия Релея. Если плоскость одной из линии существенно больше другой, то провал может отсутствовать, когда расстояние значительно больше, чем по критерию.
Зонная пластинка Френеля.
Из определения френелевских зон следует, что в данной точке наблюдения поля любые две соседние зоны действуют как источники света, колеблющееся в противофазе. Посылаемые ими волны в значительной степени гасят друг друга. Все четные зоны Френеля дают вклад в результирующее световое поле одного знака, все нечетные зоны дают вклад противоположного знака. Поэтому, если тем или иным способом «выключить» все четные, либо все нечетные зоны Френеля, можно ожидать значительного увеличения интенсивности света в точке наблюдения. Эта идея лежит в основе простого оптического устройства, называемого зонной пластинкой Френеля.


На рисунке зонная пластинка, на которой ???????? черные зоны Френеля, и соответствующая ей векторная диаграмма. Видно, что внесение зонной пластинки в световой пучок должно значительно увеличить интенсивность света в точке наблюдения, т. к. мощность света, пропускаемого пластинкой меньше мощности падающей на нее волны. Можно сделать вывод, что пластинка перераспределяет световое поле в пространстве, т. е. фокусирует свет аналогично тому, как это делает линза. Нетрудно определить фокусное расстояние зонной пластинки  , оно связано с радиусом френелевских зон соотношением:
, оно связано с радиусом френелевских зон соотношением:

Подобно линзе зонная пластинка способна строить оптическое изображение. Опыт: пучок света, ????????? с изображением, зонная пластинка, экран (на экране изображение). Перемещая зонную пластинку вдоль оси пучка, можно добиться четкого изображения на экране. Если убрать зонную пластинку с пучка, изображение исчезает. Можно усовершенствовать пластинку, заставив «работать в фазе» четные и нечетные зоны Френеля. Для этого необходимо каким-то образом ввести для каждой нечетной зоны дополнительный фазовый набег, равный  . В частности, можно изготовить профилированную («фазовую») зонную пластинку, имеющую разную толщину четных и нечетных зон. Возникает вопрос: нельзя ли вообще «распрямить» спираль векторной диаграммы, т. е. добиться предельной величины интенсивности в точке P. Очевидно, для этого необходимо плавно изменять фазу выходящей световой волны в пределах каждой зоны Френеля.
. В частности, можно изготовить профилированную («фазовую») зонную пластинку, имеющую разную толщину четных и нечетных зон. Возникает вопрос: нельзя ли вообще «распрямить» спираль векторной диаграммы, т. е. добиться предельной величины интенсивности в точке P. Очевидно, для этого необходимо плавно изменять фазу выходящей световой волны в пределах каждой зоны Френеля.


Этой цели удовлетворяет фазовая зонная пластинка с криволинейными профилями зон: зонная пластинка с криволинейным профилем собирает весь падающий на нее свет в точке Р (точнее в малой окрестности этой точки). Системы подобного типа называют плоскими линзами или растровой фокусирующей оптикой. На практике они используются, например, в прожекторах в автомобильных фарах.
Поляризация света
Поперечность световой волны.
Волновые уравнения описывают поведение произвольной компоненты вектора 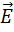 или
или  в плоской световой волне, но кроме этого, используя условие максимума, можно определить соотношения между направлениями и величинами векторов
в плоской световой волне, но кроме этого, используя условие максимума, можно определить соотношения между направлениями и величинами векторов 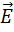 и
и  . Рассмотрим плоскую световую волну, распространяющуюся вдоль оси
. Рассмотрим плоскую световую волну, распространяющуюся вдоль оси 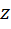 , т. е.
, т. е. 
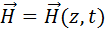 .
.
Из уравнений максимума можно показать, что в плоской электромагнитной волне, распространяющейся в свободном пространстве вдоль оси 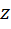 , компоненты полей в направлении распространения волны отсутствуют
, компоненты полей в направлении распространения волны отсутствуют  , т. е. волна является поперечной, кроме того, можно установить связь между отличными от 0 компонентами
, т. е. волна является поперечной, кроме того, можно установить связь между отличными от 0 компонентами  и
и  . И, рассматривая плоскую световую волну с конфигурацией поля «
. И, рассматривая плоскую световую волну с конфигурацией поля « », можно найти, что
», можно найти, что
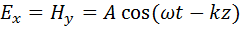 ,
,
а « »:
»:
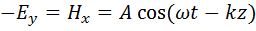

Две найденные нами поперечные волны  и
и  отличаются друг от друга направлениями векторов
отличаются друг от друга направлениями векторов 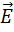 и
и  , т. е. направлениями поляризации. Волны, описываемые такими уравнениями, называются линейно поляризованными, т. к. при фиксированном значении
, т. е. направлениями поляризации. Волны, описываемые такими уравнениями, называются линейно поляризованными, т. к. при фиксированном значении 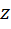 коней вектора
коней вектора 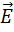 движется по прямой линии. Условимся связывать с направлением вектора
движется по прямой линии. Условимся связывать с направлением вектора 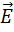 направление или вектор поляризации волны. Плоскость, в которой лежат вектор
направление или вектор поляризации волны. Плоскость, в которой лежат вектор 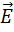 и единичный вектор
и единичный вектор 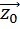 , характеризующий направление распространения волны, называется плоскостью поляризации. Линейно поляризованные волны называются также плоско поляризованными.
, характеризующий направление распространения волны, называется плоскостью поляризации. Линейно поляризованные волны называются также плоско поляризованными.
Хотя «световыми векторами» в равной мере являются векторы 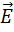 и
и  , предпочтение, отданное при определении, вектору
, предпочтение, отданное при определении, вектору 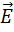 связано с тем, что сила, действующая со стороны светового поля на электрический заряд, равна:
связано с тем, что сила, действующая со стороны светового поля на электрический заряд, равна:
 ,
,
и при  действие магнитного поля много слабее, нежели электрического.
действие магнитного поля много слабее, нежели электрического.
Каждая из волн  ,
,  удовлетворяет волновому уравнению. Удовлетворяет ему и сумма этих волн. В этом состоит одно из проявлений принципа суперпозиции для световых волн в вакууме. В общем случае у плоской гармонической волны отличны от 0 обе компоненты
удовлетворяет волновому уравнению. Удовлетворяет ему и сумма этих волн. В этом состоит одно из проявлений принципа суперпозиции для световых волн в вакууме. В общем случае у плоской гармонической волны отличны от 0 обе компоненты 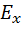 ,
, 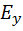 , а вектор электрического поля имеет вид:
, а вектор электрического поля имеет вид:

Рассмотрим плоскую волну, компоненты электрического поля которой изменяются по гармоническому закону:
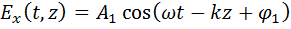

тогда уравнение траектории, по которой движется конец вектора 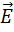 в плоскости
в плоскости  :
:
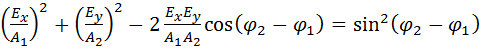 –
–
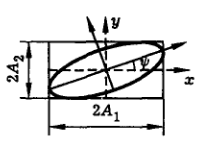
Это уравнение называется уравнением эллипса. Эллипс вписан в прямоугольник, стороны которого параллельны осям  и имеют длины
и имеют длины  и
и  . Итак, в общем случае при распространении плоской монохроматической световой волны конец вектора
. Итак, в общем случае при распространении плоской монохроматической световой волны конец вектора 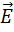 в плоскости
в плоскости  описывает эллипс. Аналогично ведет себя вектор напряженности магнитного поля. Такая волна называется эллиптически поляризованной. Двигаясь по эллипсу в плоскости
описывает эллипс. Аналогично ведет себя вектор напряженности магнитного поля. Такая волна называется эллиптически поляризованной. Двигаясь по эллипсу в плоскости  , конец вектора
, конец вектора 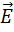 может вращаться по часовой или против часовой стрелки. Для того, чтобы различить эти два состояния, в оптике вводят понятие правой поляризации (для наблюдателя, смотрящего навстречу световому лучу, вращение вектора
может вращаться по часовой или против часовой стрелки. Для того, чтобы различить эти два состояния, в оптике вводят понятие правой поляризации (для наблюдателя, смотрящего навстречу световому лучу, вращение вектора 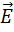 происходит по часовой стрелке) и левой поляризации (вращение вектора
происходит по часовой стрелке) и левой поляризации (вращение вектора 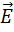 в противоположном направлении).
в противоположном направлении).
Направление вектора 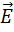 зависит от знака разности фаз
зависит от знака разности фаз 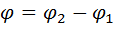 . Выберем момент времени
. Выберем момент времени 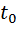 , для которого >
, для которого >  . В этот момент, согласно
. В этот момент, согласно  ,
, 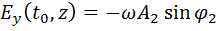 . В этот момент, когда конец вектора
. В этот момент, когда конец вектора 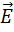 достигает крайней правой точки своей траектории, имеем
достигает крайней правой точки своей траектории, имеем 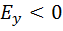 , если
, если 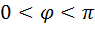 , и
, и 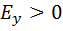 , если
, если  . Первый случай соответствует право поляризованной волне, второй – лево поляризованной.
. Первый случай соответствует право поляризованной волне, второй – лево поляризованной.
Далее рассмотрим частные случаи.
Линейная поляризация.
Если разность фаз 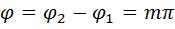 , то эллипс переходит в прямую, описывающуюся уравнением:
, то эллипс переходит в прямую, описывающуюся уравнением:
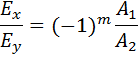
В этом случае волна является линейно или плоско поляризованной. Два возможных направления соответствуют 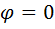 и
и 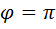 .
.

Круговая поляризация.
Если 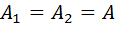 и
и 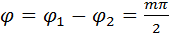 , где r w:val="000000"/><w:sz w:val="32"/></w:rPr><m:t>m=В±1, В±3, В±5…</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, где r w:val="000000"/><w:sz w:val="32"/></w:rPr><m:t>m=В±1, В±3, В±5…</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  , то одна из компонент вектора
, то одна из компонент вектора 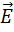 проходит через максимум в тот момент, когда другая обращается в 0. В этом случае эллипс вырождается в окружность, которая описывается уравнением:
проходит через максимум в тот момент, когда другая обращается в 0. В этом случае эллипс вырождается в окружность, которая описывается уравнением:

Конец вектора 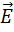 (и
(и  ) движется по окружности, вращаясь по и против часовой стрелки. Такое состояние поляризации называется круговой или циркулярной. Различают правую и левую круговые поляризации. Для правой поляризации:
) движется по окружности, вращаясь по и против часовой стрелки. Такое состояние поляризации называется круговой или циркулярной. Различают правую и левую круговые поляризации. Для правой поляризации:
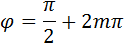




Для левой поляризации:

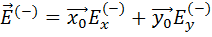
Из формул видно, что
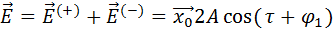 ,
,
т. е. сумма право и лево-поляризованных волн дает линейно-поляризованную волну.

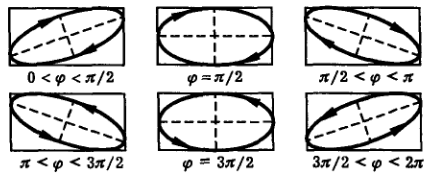
Эллиптически поляризованная волна при разных значениях разности фаз  ортогональных компонент поля.
ортогональных компонент поля.
Параметры Стокса. Сфера Пуанкаре.
В общем случае плоская монохроматическая световая волна имеет правую и левую эллиптическую поляризацию. Полная характеристика эллипса дается тремя параметрами, направлениями 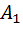 ,
, 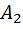 ,
,  или выражающимися через них полуосями эллипса
или выражающимися через них полуосями эллипса  ,
, 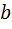 и углом
и углом  между осью
между осью 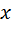 и большой осью эллипса. Удобно также описание эллиптически поляризованной волны на основе параметров Стокса, определяемых формулами:
и большой осью эллипса. Удобно также описание эллиптически поляризованной волны на основе параметров Стокса, определяемых формулами:



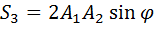
Независимыми оказываются только три из них, т. к. справедливо тождество:
 ,
,
вводя вспомогательный угол 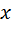 , определяемый формулой:
, определяемый формулой:
 ,
,
где  и
и 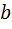 - полуоси эллипса. «+» соответствует правой, а «
- полуоси эллипса. «+» соответствует правой, а «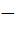 » - лево-поляризованной волне. Нетрудно получить:
» - лево-поляризованной волне. Нетрудно получить:
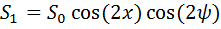
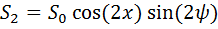

Их этих формул можно пояснить физический смысл параметров Стокса. Параметр  представляет собой интенсивность поляризованной волны;
представляет собой интенсивность поляризованной волны;  - параметр преимущественной горизонтальной поляризации, т. к. он повышается с ростом
- параметр преимущественной горизонтальной поляризации, т. к. он повышается с ростом 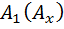 и уменьшением
и уменьшением  ;
; 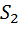 - параметр преимущественной диагональной поляризации;
- параметр преимущественной диагональной поляризации; 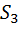 - параметр преимущественной правой циркулярной поляризации. Формулы для параметров Стокса могут быть положены в основу наглядного геометрического представления поляризации.
- параметр преимущественной правой циркулярной поляризации. Формулы для параметров Стокса могут быть положены в основу наглядного геометрического представления поляризации.
Параметры Стокса 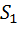 ,
, 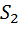 и
и 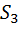 можно рассматривать как декартовы координаты точки на сфере радиуса
можно рассматривать как декартовы координаты точки на сфере радиуса 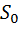 , углы
, углы  и
и  имеют смысл сферических угловых координат этой точки. Угол
имеют смысл сферических угловых координат этой точки. Угол  характеризует ориентацию эллипса поляризации, угол
характеризует ориентацию эллипса поляризации, угол 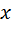 - его эллиптичность (отношение полуосей) и направление вращения. Такое геометрическое решение предложил Пуанкаре, поэтому сферу называют Пуанкаре.
- его эллиптичность (отношение полуосей) и направление вращения. Такое геометрическое решение предложил Пуанкаре, поэтому сферу называют Пуанкаре.

При описании положения точки на сфере обычно используют географическую топологию, т. е. верхняя  и нижняя
и нижняя 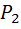 точки сферы называются полюсами, а различные окружности в сечении сферы – меридианами, параллелями и экватором.
точки сферы называются полюсами, а различные окружности в сечении сферы – меридианами, параллелями и экватором.
Верхний полюс соответствует левоциркулярно поляризованному свету, нижний – правоциркулярно поляризованному свету. Точки на экваторе соответствуют линейной поляризации с плавно меняющимся от точки к точке азимутом. Точку Н на экваторе, соответствующую горизонтальной поляризации, выбирают за начало отсчета. Диаметрально противоположная точка экватора будет определять вертикальную линейную поляризацию. Все остальные точки поверхности сферы представляют различные формы эллиптической поляризации. При этом по долготе меняется эллиптичность, а по широте – ориентация эллипса поляризации. Если передвигаться по одному выбранному меридиану от верхнего полюса к нижнему, то в верхнем полушарии пройдем последовательно через все более вытянутые эллипсы с левым вращением электрического вектора и на экваторе попадем в точку с линейной поляризацией, следуя далее по тому же меридиану в нижнее полушарие, постепенно пройдем через все возможные эллипсы с правым вращением и уменьшающейся эллиптичностью вплоть до правоциркулярного поляризованного света на нижнем полюсе. Перемещаясь, пройдем через все возможные ориентации эллипса с одной и той же эллиптичностью и вернемся к исходной. Таким образом, различные возможные состояния поляризации можно изобразить на сфере Пуанкаре. Существенно, что параметры Стокса имеют размерность интенсивности и могут быть непосредственно определены экспериментально. Т. е. любому состоянию поляризации соответствует точка на сфере Пуанкаре.
Более того, с помощью параметров Стокса можно представить и не полностью поляризованное излучение. Для такого излучения:
 .
.
В общем случае не полностью поляризованное излучение можно разложить на две компоненты: полностью поляризованную и неполяризованную, т. е.

И каждый параметр Стокса исходного пучка равен сумме соответствующих параметров составляющих пучков  и
и  . При описании не полностью поляризованного света вводится понятие о степени поляризации, которая определяется как отношение интенсивности полностью поляризованной компоненты к оющей интенсивности пучка:
. При описании не полностью поляризованного света вводится понятие о степени поляризации, которая определяется как отношение интенсивности полностью поляризованной компоненты к оющей интенсивности пучка: