Теорема Вейерштрасса. (Основная теорема теории последовательностей).
Если последовательность 
является нестрого возрастающей (нестрого убывающей) и ограничена сверху (снизу), то является сходящейся.
Данную теорему можно сформулировать немного иначе - Любая монотонная и ограниченная последовательность имеет предел.
Определение. Последовательность 
называется
- монотонно возрастающей (неубывающей), если 
;
- строго монотонно возрастающей (неубывающей), если 
;
- монотонно убывающей (невозрастающей), если 
;
- строго монотонно убывающей (невозрастающей), если 
;
Монотонно возрастающие последовательности обозначают символом 
, монотонно убывающие - символом 
.
Сейчас докажем одну из важнейших теорем.
Теорема:
1. Если последовательность 
монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
2. Если последовательность монотонно возрастает, но неограниченна сверху, то 
.
Доказательство.
Часть 1. Пусть 
ограниченны сверху, т.е. 
такое, что 
. Тогда, согласно теореме о существовании супремума мы можем утверждать, что 
.
Вспомним свойства 
. Их было два
Но учтем теперь что . Это значит, что 
. Тогда имеем следующую цепочку неравенств
Выбрасывая лишнее получим, что 
или 
, что и говорит о том, что 
.
Заметьте, что предел равен как раз супремуму множества .
Часть 2. Пусть теперь неограниченна сверху. Это значит, что 
.
Но . Значит, и поэтому можно записать 
. Выбрасывая в этом неравенстве 
, получим окончательно
что и говорит о том, что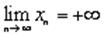 
.
65. Число e.
Число е – непрерывное число=2.72.. Число е принято за основание натуральных логарифмов: логарифм по основанию е называется натуральным логарифмом и обозначается lnx. Если знак не меняется – последовательность монотонная.
Прежде чем переходить к знаменитому в математике числу e, дадим без вывода одну железную формулу, которая называется биномом Ньютона.
Напомним, что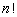 
(читается: n - факториал) есть произведение целых чисел от 1 до 
:
По определению считается 
.
Выражение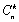 
(читается 
из 
по 
)
называется биноминальным коэффициентом. Другое выражение для
имеет вид
В частности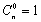 
, 
, 
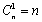и т.д.
Бином Ньютона имеет вид
или в более явном виде
Отсюда легко получаются известные из школьного курса выражения для 
, 
, 
и т.д.
Рассмотрим теперь последовательность с членами
, 
.
1. Получим другое выражение для . Используя формулу бинома Ньютона, получим 
.
2. Покажем, что . Для этого запишем рядом и 
.
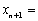
Так как 
, то 
, 
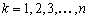. Поэтому каждое слагаемое в 
больше соответствующего слагаемого в . Кроме того, в есть “лишние” положительные слагаемое
которого не было в . Поэтому 
.
3. Покажем теперь, что ограничена сверху.
Действительно, так как 
, то
.
Но так как
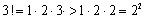
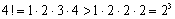
и вообще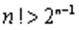 
то 
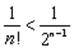< и
где в процессе выкладок использована формула для суммы геометрической прогрессии.
Итак, 
монотонно возрастает и 
. Поэтому существует 
который и называется числом e.
.
Предел и односторонние пределы функции. Основные понятия и определения.
Предел функции (предельное значение функции) — одно из основных понятий математического и функционального анализов. Предел - это значение, к которому функция в определённом смысле приближается при приближении аргумента к определённой точке.
1. Ограниченность функции.
Функция f(x) называется ограниченной на данном отрезке (a,b),если существует некоторые числа m и M такие, что m ≤ f(x) ≤ M при x є (a, b).
Число m0 = inf{f(x)} = max(m) при x є (a, b) называется нижней гранью функции f(x), а число M0 = =sup{f(x)} = min(M) при x є (a, b) называется верхней гранью функции f(x) на данном промежутке (a, b). Разность M0 – m0 называется колебанием функции на промежутке (a, b).
2. Предел функции в точке.
Пусть функция f(x) определена на множестве X = {x}, имеющем точку сгущения a. Запись
(1)
обозначает, что для каждого числа ε > 0 существует число δ = δ(ε) > 0 такое, что для всех x, для которых f(x) имеет смысл и которые удовлетворяют условию 0 <|x - a|< δ, справедливо неравенство |f(x) – A| < ε.
Для существования предела функции (1) необходимо и достаточно, чтобы для каждой последовательности xn → a, xn ≠ a (xn є X; n = 1, 2, …), было выполнено равенство
.
Имеют место два замечательных предела:
1) 
, 2) 
.
Критерий Коши. Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0 найдется δ = δ(ε) > 0 такое, что |f(x’) – f(x’’)| < ε,
Как только 0<|x’ - a|<δ и 0<|x’’ - a|<δ, где x’ и x’’ – любые точки из области определения функции f(x).
3. Односторонние пределы.
Число A’ называется пределом слева функции f(x) в точке a:
A’ = 
,
если |A’ – f(x)| < ε при 0 < a – x < δ(ε).
Аналогично, число A’’ называется пределом справа функции f(x) в точке a:
A’' = 
,
если |A’’ – f(x)| < ε при 0 < x – a < δ(ε).
Для существования предела функции f(x) в точке a необходимо и достаточно, чтобы
f(a – 0) = f(a + 0).
4. Бесконечный предел.
Условная запись
обозначает, что для любого E > 0 справедливо неравенство:
|f(x)| > E, если только 0 < |x – a|< δ(ε).
5. Частичный предел.
Если для некоторой последовательности xn a (xn ≠ a) имеет место равенство
,
то число (или символ) B называется частичным пределом (соответственно конечным или бесконечным) функции f(x) в точке a.
Наименьший или наибольший из этих частичных пределов обозначаются через
и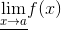 
и называются соответственно нижним и верхним пределами функции f(x) в точке a.
Равенство
=
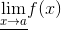
необходимо и достаточно для существования предела(соответственно конечного и бесконечного) функции f(x) в точке a.