Мы будем рассматривать евклидовое векторное линейное пространство, в котором изучаются прямая линия и плоскость.
При изучении линейного пространства было введено понятие подпространства, определенное как линейное пространство, состоящее, может быть, из меньшего числа базисных векторов. Это означает, что все свойства пространства выполняются и для подпространства. В частности, любое подпространство должно содержать нуль-вектор. Если в линейном пространстве введена система координат, то не всякая прямая линия и плоскость образуют подпространство. Ими будут прямая и плоскость, проходящие через начало. Этот факт говорит о том, что для изучения различных видов прямых и плоскостей необходимо введение координатной системы.
Пусть на плоскости зафиксирована декартова система координат Oxy и задана в ней прямая l (рис. V.4). Пусть дан ненулевой вектор 
перпендикулярный прямой l, то есть 
. Вектор 
назовем нормальным (или нормалью) для прямой l. Все другие нормальные векторы к l будут коллинеарны вектору .
Рис. V.4.
Пусть точка 
– точка на прямой. Любая из точек 
прямой обладает тем свойством, что векторы 
и перпендикулярны, поэтому их скалярное произведение
. (V.1)
Так как 
, то из формулы (V.1) получаем
или
, (V.2)
где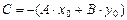 
.
Уравнение называется общим уравнением прямой, так как всякое уравнение вида (V.2) определяет прямую, и наоборот.
Рассмотрим линейную функцию двух переменных. Пусть ее вид
. (V.3)
Но этой функции «тесно» на плоскости. Пусть дано линейное векторное трехмерное пространство ﻉ. Введем декартову систему координат Oxyz и по аналогии с предыдущим зададим нормальный вектор 
. Поскольку областью определения уравнения (V.3) является геометрическая плоскость, то уравнение (V.3) определяет плоскость P в пространстве и 
.
После задания точки 
, учитывая условие перпендикулярности векторов, для любой точки 
, лежащей на плоскости P, аналогично будем иметь
, (V.4)
обозначая 
, получаем уравнение (V.3), которое назовем общим уравнением плоскости. Таким образом, по заданному нормальному вектору и точке 
на прямой l мы однозначно можем определить прямую на плоскости и плоскость в пространстве.
Выясним, как связаны между собой два общих уравнения, определяющие одну и ту же плоскость или прямую.
Пусть имеем систему
(V.5)
, 
и ненулевые нормальные векторы 
, 
. Так как все нормальные векторы к заданной точке коллинеарны, то их координаты пропорциональны, то положим, например,
или, что то же самое,
, 
, 
, 
.
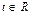Умножая второе уравнение формулы (V.5) на t и складывая с первым, получим
.
Вывод: коэффициенты общих уравнений одной плоскости пропорциональны.
Определение. Общее линейное уравнение называется полным если все его коэффициенты ненулевые.
Пример V.3. 1) По внешнему виду уравнения (V.5) могут быть полными.
2) Уравнение плоскости (рис. V.5)
соответствует определению и потому полное.
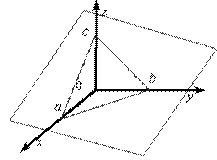
Рис. V.5
Пример V.4. Составить уравнение плоскости, проходящей через точку 
и перпендикулярной вектору 
.
Решение. Используя формулу (V.4), имеем 
, откуда после преобразований получим 
.
Это уравнение первой степени и есть искомое уравнение плоскости.