4.3.1. Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено не более трех изделий.
4.3.2. Автоматическая штамповка клемм для предохранителей дает 10% отклонений от принятого стандарта. Сколько стандартных клемм следует ожидать с вероятностью 0,0587 среди 400 клемм?
4.3.3. При передаче сообщения вероятность искажения одного знака равна 1/100. В предположении независимости искажения знаков найти вероятность того, что сообщение из 5 знаков: а) не будет искажено; б) содержит ровно одно искажение; в) содержит хотя бы одно искажение.
4.3.4. Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.
4.3.5. Игральную кость (шестигранный кубик) подбрасывают 100 раз. Найти наивероятнейшее число выпадений “6” и вероятность такого результата.
4.3.6. Вероятность появления положительного результата в каждом из n опытов равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат.
4.3.7. Посеяно 600 семян кукурузы с вероятностью р =0,9 произрастания. Найти абсолютную величину отклонения частости взошедших семян от вероятности, если это отклонение должно быть гарантировано с вероятностью р 0=0,995.
4.3.8. Технический контроль проверяет из партии в 400 деталей 40, взятых наудачу. Партия содержит 8 бракованных деталей. Какого наиболее вероятное число нестандартных деталей в выборке и какова соответствующая вероятность?
4.3.9. Из каждого десятка деталей 9 удовлетворяют стандарту. Найти вероятность того, что из 50 взятых со склада деталей число стандартных окажется между 42 и 48.
4.3.10. Вероятность появления события в каждом из независимых испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях будет равно 30.
4.4.; 4.5. Случайные величины.
4.4.1. Закон распределения дискретной случайной величины X задан следующей таблицей:
| X | ||||
| P | 1/16 | 1/4 | 1/2 | 3/16 |
Найти М (Х), s(Х) и Р (Х >2).
4.4.2. Вероятность появления события в каждом из независимых испытания равна 0,8. Составить таблицу распределения чисел появлений события при 3 испытаниях. Найти математическое ожидание и среднее квадратическое отклонение данной случайной величины.
4.4.3. В урне 6 белых и 4 черных шара. Из урны извлекается шар 5 раз подряд, причем каждый раз вынутый шар возвращается в урну и шары перемешиваются. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения для величины Х, найти М (Х) и D (X).
4.4.4. В урне имеется 4 шара с номерами 1,2,3,4. Вынуты 2 шара. Случайная величина Х – сумма номеров шаров. Найти закон распределения случайной величины Х, М (Х), Р (Х >5).
4.4.5. Найти математическое ожидание и дисперсию числа очков при одном бросании игральной кости и суммы очков при бросании двух игральных костей.
4.4.6. Трижды подбрасывается правильная монета. Случайная величина Х – число выпавших гербов. Найти закон распределения данной случайной величины, М (Х), Р (Х ³2).
4.4.7. Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна р. Рассматриваются случайные величины:
Х – разность между числом попаданий и числом промахов;
Y – сумма числа попаданий и числа промахов.
Найти закон распределения для каждой случайной величины Х, Y, M (X), D (X), M (Y), D (Y).
4.4.8. Дискретная случайная величина Х имеет только три возможных значения: х 1=1, х 2 и х 3, причем х 1< х 2< х 3. Вероятности того, что х примет значения х 1 и х 2, соответственно равны 0,3 и 0,2. Найти закон распределения величины Х, зная ее математическое ожидание М (Х)=2,2 и дисперсию D (X)=0,76.
4.4.9. Дискретная случайная величина Х имеет только два возможных значения: х 1 и х 2, причем х 1< х 2. Вероятность того, что Х примет значения х 1, равна 0,2. Найти закон распределения Х, зная математическое ожидание М (Х)=2,6 и среднее квадратическое отклонение s(Х)=0,8.
4.4.10. Брошены n игральных костей. Найти дисперсию суммы чисел очков, которые могут появиться на всех выпавших гранях.
4.5.1. Случайная величина Х имеет плотность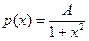 
. Найти коэффициент А, функцию распределения F (х), вероятность неравенств –1< X <1, M (X).
4.5.2. Случайная величина X имеет плотность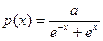 
. Найти постоянную величину а и вероятность того, что в двух независимых наблюдениях Х примет значения, меньшие единицы.
4.5.3. Случайная величина X имеет плотность
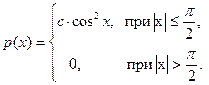
Найти коэффициент с, М (Х), D (X).
4.5.4. Случайная величина Х задана функцией распределения
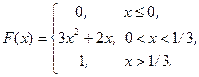
Найти плотность распределения вероятностей, M (X), D (X), вероятность Р (Х >1/6). Построить графики р (х) и F (x).
4.5.5. Случайная величина Х распределена по закону Релея, т.е. имеет плотность
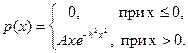
Найти коэффициент А, функцию распределения F (x), M (Х), D (Х).
4.5.6. Мишень состоит из трех концентрических кругов радиусом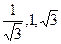 
. Попадание в центральный круг стоит 4 очка, в среднее кольцо – 3, в крайнее кольцо – 2 и вне кругов – 0 очков. Вероятность попадания на расстоянии r от центра мишени равна 
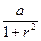. Найти коэффициент а и математическое ожидание числа очков, выбитых при пяти выстрелах.
4.5.7. Случайная величина Х в интервале (-3, 3) задана плотностью распределения
.
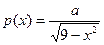Вне этого интервала р (х)=0. Найти коэффициент а, функцию распределения F (x). Что вероятнее: в результате испытания окажется X <1 или Х >1?
4.5.8. Плотность случайной величины Х имеет вид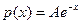 
при х ³0 и р (х)=0 при х <0. Найти коэффициент А, функцию распределения F (x), M (Х), D (Х).
4.5.9. Случайная величина X задана функцией распределения
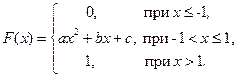
Выбрать коэффициенты а, b и c таким образом, чтобы данное распределение соответствовало случайной величине непрерывного типа, написать выражение для плотности р (х).
4.5.10. Случайная величина X подчинена закону Лапласа:
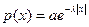(l >0).
а) найти коэффициент а; б) построить графики плотности распределения и функции распределения; в) найти M (Х), D (Х).
4.6. Закон больших чисел.
4.6.1. Вероятность появления события в каждом испытании постоянна и равна 0,8. Произведено 900 испытаний. Какова вероятность того, что отклонение относительной частоты появления события от вероятности 0,8 по абсолютной величине не превзойдет 0,05?
4.6.2. Вероятность наступления некоторого события в каждом из 1000 испытаний равна 0,2. Используя неравенство Чебышева, оценить вероятность того, что отклонение числа наступлений этого события от математического ожидания будет не более 20.
4.6.3. В урне 100 белых и 100 черных шаров. Вынули с возвращением 50 шаров. Оценить сверху вероятность того, что количество белых шаров, из числа вынутых, удовлетворяет двойному неравенству 15< m <35.
4.6.4. В результате 200 независимых опытов найдены значения случайной величины x 1, x 2, …, x 200, причем M (Х)= D (Х)=2. Оценить сверху вероятность того, что абсолютная величина разности между средним арифметическим значений случайной величины и математическим ожиданием меньше 1/5.
4.6.5. Дискретная случайная величина задана законом распределения
| Х | ||
| Р | 0,2 | 0,8 |
Используя неравенство Чебышева, оценить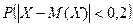 
.
4.6.6. Непрерывная случайная величина Х имеет плотность распределения
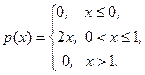
С помощью неравенства Чебышева оценить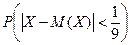 
.
4.6.7. Дано: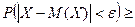 
0,9 и D (X)=0,009. Используя неравенство Чебышева, найти e.
4.6.8. Дисперсия каждой из 2500 независимых случайных величин с одним и тем же математическим ожиданием не превосходит 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от их математического ожидания не превзойдет 0,4.
4.6.9. Сколько раз нужно бросить игральную кость, чтобы с вероятностью, не меньшей 0,99, частота появления шести очков отклонялась по абсолютной величине от вероятности этого события в одном испытании не более чем на 0,01?
4.6.10. Сколько раз нужно подбросить монету, чтобы с вероятностью, не меньшей 0,975, утверждать, что частота выпадения герба попадает в интервал (0,4; 0,6)?
4.7. Система двух случайных величин.
4.7.1.-4.7.5 Проверить независимость дискретного случайного вектора, заданного таблицей вероятностей.
4.7.1.
| X \ Y | |||
| –3 | 0,05 | 0,1 | 0,05 |
| 0,2 | 0,4 | 0,2 |
4.7.2.
| X \ Y | |||
| 0,1 | 0,03 | 0,42 | |
| 0,15 | 0,15 | 0,5 |
4.7.3.
| X \ Y | |||
| 0,5 | 0,04 | 0,06 | 0,2 |
| 0,25 | 0,35 | 0,1 |
4.7.4.
| X \ Y | |||
| 0,6 | 0,04 | 0,16 | |
| 0,06 | 0,08 | 0,06 |
4.7.5.
| X \ Y | |||
| 0,2 | 0,06 | 0,5 | |
| 0,05 | 0,1 | 0,09 |
4.7.6.-4.7.10 Случайный вектор (X, Y) имеет равномерное распределение в области D, т.е. его плотность
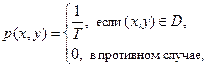
где Т – площадь области D. Проверить независимость вектора (X, Y), если:
4.7.6. D – треугольник с вершинами (0,0), (0,1), (1,0);
4.7.7. D – квадрат с вершинами (1,0), (0,1), (-1,0), (0,-1);
4.7.8. D – прямоугольник с вершинами (0,0), (0,1), (2,1), (2,0);
4.7.9. D – прямоугольник с вершинами (2,4), (0,4), (0,0), (2,0);
4.7.10. D – квадрат с вершинами (1,1), (-1,1), (-1,-1), (1,-1).
Вопросы к экзамену по теме 4 “ Теория вероятностей ”
1. Математическая схематизация случайных явлений. Пространство элементарных событий.
2. Случайные события, операции над событиями и отношения между ними.
3. Аксиомы теории вероятностей. Частота события, ее связь с вероятностью, свойства частот.
4. Следствия из аксиом теории вероятностей: вероятность противоположного события, вероятность суммы событий.
5. Вероятностные пространства. Классическое определение вероятности.
6. Формулы комбинаторики.
7. Определение условных вероятностей. Независимость событий. Вероятность произведения событий.
8. Формулы полной вероятности. Формула Байеса.
9. Последовательность независимых испытаний. Схема Бернулли.
10. Предельные теоремы Муавра-Лапласа и Пуассона.
11. Определение случайной величины. Функция распределения и ее свойства.
12. Дискретные распределения. Биномиальное распределение, распределение Пуассона.
13. Непрерывные распределения. Функция плотности распределения и ее свойства.
14. Примеры непрерывных распределений: равномерное, показательное, нормальное.
15. Математическое ожидание случайной величины, свойства и вероятностный смысл математического ожидания.
16. Дисперсия и среднее квадратическое отклонение случайной величины. Свойства и вероятностный смысл дисперсии.
17. Системы случайных величин. Функция распределения двумерного случайного вектора, закон распределения компонент вектора. Независимость случайных величин, входящих в систему.
18. Функция плотности распределения непрерывного случайного вектора, частные плотности компонент вектора и их независимость.
19. Числовые характеристики системы случайных величин: математическое ожидание и дисперсия составляющих. Свойства числовых характеристик.
20. Корреляционный момент, коэффициент корреляции. Взаимосвязь между понятиями коррелированности и зависимости случайных величин.
21. Неравенство Чебышева, теорема Чебышева. Теорема Бернулли.