При этом методе задача (4.2.1) заменяется на задачу
F (X, rs)= f (X)+ P (X, rs) ® min, (4.3.2)
где
P (X, rs)= 
,
=max{0, 
}= 
,
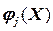rs - так называемый параметр штрафа. Функция P (X, rs) называется штрафной функцией. К полученной задаче применяются численные методы безусловной оптимизации (нулевого, первого или второго порядков). При этом начальная точка поиска задаётся обычно вне множества допустимых решений X. На каждой s -й итерации ищется точка X *(rs) минимума вспомогательной функции F (X, rs) при заданном параметре rs с помощью одного из методов безусловной минимизации. Полученная точка X *(rs) используется в качестве начальной на следующей итерации, выполняемой при возрастающем значении параметра штрафа. При неограниченном возрастании rs последовательность точек X *(rs) стремится к точке условного минимума X *.
Более подробно:
1. Задать: начальную точку X 0 внутри области X; начальное значение параметра rs ³0; число C >1 для уменьшения параметра штрафа; малое число e ³0 для остановки алгоритма. Положить s =0.
2. Составить вспомогательную функцию
F (X, rs)= f (X)+ .
3. Найти точку X *(rs) безусловного экстремума функции F (X, rs) по X с помощью какого-либо метода (нулевого, первого или второго порядка):
F (X *(rs), rs)= 
F (X, rs).
При этом задать все требуемые выбранным методом параметры. В качестве начальной точки взять Xs. Вычислить P (X *(rs), rs).
4. Проверить условие окончания:
а) если P (X *(rs), rs)£ e, то процесс поиска закончить:
X *= X *(rs), f (X *)= f (X *(rs));
б) если P (X *(rs), rs)< e, то положить: rs +1= Crs, Xs +1= X *(rs), s = s +1 и перейти к шагу 2.
Обычно выбирается r 0Î{0,01; 0,1; 1}, а C Î[4, 10].
Пример I. Исследовать на условный экстремум функцию:
f (X)= 
® min
3 x 1-2 x 2-5=0.
Решение. Нам потребуется вспомогательная функция F (X, rs) при различных значениях параметра rs и её градиент. Поэтому предварительно выпишем эти элементы задачи в общем виде:
F (X, rs)= + 
(3 x 1-2 x 2-5)2,
=4 x 1+3 rs (3 x 1-2 x 2-5), 
=8 x 2-2 rs (3 x 1-2 x 2-5),
Ñ F (X, rs)=(4 x 1+3 rs (3 x 1-2 x 2-5), 8 x 2-2 rs (3 x 1-2 x 2-5)).
Далее действуем пошагово согласно вышеописанной схеме.
Шаг 1. Зададим: начальную точку X 0=(1, -1) внутри области X; начальное значение параметра rs =0,1; число C =4 для уменьшения параметра штрафа; малое число e =0,1 для остановки алгоритма. Положить s =0.
Шаг 2. Составим вспомогательную функцию
F (X; 0,1)= +0,05×(3 x 1-2 x 2-5)2.
Шаг 3. Найдём точку X *(0,1) безусловного минимума функции F (X, 0,1) по X с помощью метода градиетного спуска:
F (X *(0,1), 0,1)= +0,05×(3 x 1-2 x 2-5)2 ® min (4.3.3)
1. Зададим X 0=(1, -1), e 1=0,1, e 2=0,1, k 0=10, найдём градиент
Ñ F (X; 0,1)=(4 x 1+0,3×(3 x 1-2 x 2-5), 8 x 2-0,2×(3 x 1-2 x 2-5)).
2. Положим k =0.
3.0. Вычислим Ñ F (X 0; 0,1)=(4; -8).
4.0. Вычислим |Ñ F (X 0; 0,1)| и проверим критерий окончания: |Ñ F (X 0; 0,1)|=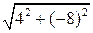 
»8,9443>0,1. Переходим к шагу 5.
5.0. Проверим условие k > k 0: k =0<10= k 0. Переходим к шагу 6.
6.0. Зададим h 0=0,1.
7.0. Вычислим X 1= X 0-0,1× F (X 1; 0,1)=(1; -1)-0,1×(4; -8)=(0,6; -0,2).
8.0. Проверим выполнение условия F (X 1; 0,1)- F (X 0; 0,1)<0. Так как F (X 1; 0,1)=1,272, F (X 0; 0,1)=7, то условие выполняется. Переходим к шагу 9.
9.0. Проверим условия r (X 1, X 0)<0,1 и | F (X 1; 0,1)- F (X 0; 0,1)|<0,1. Второе условие не выполняется: | F (X 1; 0,1)- F (X 0; 0,1)|=4,728>0,1. Полагаем k =1 и переходим к шагу 3.
3.1. Вычислим Ñ F (X 1; 0,1)=(1,56; -1,04).
4.1. Вычислим |Ñ F (X 1; 0,1)| и проверим критерий окончания: |Ñ F (X 1; 0,1)|= 
»1,8749>0,1. Переходим к шагу 5.
5.1. Проверим условие k > k 0: k =1<10= k 0. Переходим к шагу 6.
6.1. Зададим h 1=0,1.
7.1. Вычислим X 2:
X 2= X 1-0,1×Ñ F (X 1; 0,1)=(0,6; -0,2)-0,1×(1,56; -1,04)=(0,444; -0,096).
8.1. Проверим выполнение условия F (X 2; 0,1)- F (X 1; 0,1)<0. Так как F (X 2; 0,1)=1,0353, F (X 1; 0,1)=1,272, то условие выполняется: F (X 2; 0,1)- F (X 1; 0,1)=1,0353-1,272=-0,2367. Переходим к шагу 9.
9.1. Проверим условия r (X 2, X 1)<0,1 и | F (X 2; 0,1)- F (X 1; 0,1)|<0,1. Второе условие не выполняется: | F (X 2; 0,1)- F (X 1; 0,1)|=0,2367>0,1. Полагаем k =2 и переходим к шагу 3.
3.2. Вычислим Ñ F (X 2; 0,1)=(0,7332; -0,0728).
4.2. Вычислим |Ñ F (X 2; 0,1)| и проверим критерий окончания: |Ñ F (X 2; 0,1)|= 
=0,7368>0,1. Переходим к шагу 5.
5.2. Проверим условие k > k 0: k =2<10= k 0. Переходим к шагу 6.
6.2. Зададим h 2=0,1.
7.2. Вычислим X 3:
X 3= X 2-0,1×Ñ F (X 2; 0,1)=(0,444; -0,096)-0,1×(0,7332; -0,0728)=(0,3707;-0,0887).
8.2. Проверим выполнение условия F (X 3; 0,1)- F (X 2; 0,1)<0. Так как F (X 3; 0,1)=0,9947, F (X 2; 0,1)=1,0353, то условие выполняется: F (X 3; 0,1)- F (X 2; 0,1)=-0,0406. Переходим к шагу 9.
9.2. Проверим условия r (X 3, X 2)<0,1 и | F (X 3; 0,1)- F (X 2; 0,1)|<0,1. Оба условия выполняются:
r (X 3, X 2)= 
=0,0737<0,1,
| F (X 3; 0,1)- F (X 2; 0,1)|=0,0406<0,1.
Это значит, X *(0,1)=(0,3707; -0,0887) - решение задачи (4.3.3).
Вычислим P (X *(0,1), 0,1)=0,05×(3×0,3707-2×(-0,0887)-5)2=0,6941.
Шаг 4. Проверить условие окончания:
а) если P (X *(rs), rs)£ e, то процесс поиска закончить:
X *= X *(rs), f (X *)= f (X *(rs));
б) если P (X *(rs), rs)> e, то положить: rs +1= Crs, Xs +1= X *(rs), s = s +1 и перейти к шагу 2.
Имеем P (X *(0,1), 0,1)=0,6941>0,1. Поэтому полагаем r 1= C × r 0=4×0,1=0,4, X 0= X *(0,1)=(0,3707; -0,0887), и перейти к шагу 2, то есть решаем задачу
F (X *(0,4), 0,4)= +0,2×(3 x 1-2 x 2-5)2 ® min (4.3.4)
Ниже приводим только результаты пунктов алгоритма без комментариев:
1. X 0=(0,3707; -0,0887), e 1=0,1, e 2=0,1, k 0=10,
Ñ F (X; 0,4)=(4 x 1+1,2×(3 x 1-2 x 2-5), 8 x 2-0,8×(3 x 1-2 x 2-5)).
2. k =0.
3.0. Ñ F (X 0; 0,4)=(-2,9698; 2,2588).
4.0. |Ñ F (X 0; 0,4)|»3,7312>0,1.
5.0. k > k 0? k =0<10= k 0. ® 6.
6.0. h 0=0,1.
7.0. X 1=(0,6677; -0,3146).
8.0. F (X 1; 0,1)- F (X 0; 0,1)=-0,6511<0. ® 9.
9.0. | F (X 1; 0,1)- F (X 0; 0,1)|= 0,6511>0,1. k =1 и ® 3.
3.1. Ñ F (X 1; 0,1)=(-0,1704; -0,6226).
4.1. |Ñ F (X 1; 0,1)|»0,6456>0,1. ® 5.
5.1. k > k 0? k =1<10= k 0. ® 6.
6.1. h 1=0,1.
7.1. X 2=(0,6847; -0,2523).
8.1. F (X 2; 0,1)- F (X 1; 0,1)=-0,0245. ® 9.
9.1. r (X 2, X 1)=0,0646<0,1 и | F (X 2; 0,1)- F (X 1; 0,1)|=0,0245<0,1.
Значит, X *(0,4)=(0,6847; -0,2523) - решение задачи (4.3.4).
Вычислим P (X *(0,4), 0,4)=1,1212.
Шаг 4. Проверим условие окончания: P (X *(0,4), 0,4)=1,1212>0,1. Поэтому полагаем r 2= C × r 1=4×0,4=1,6, X 0= X *(0,4)=(0,6847; -0,2523), и переходим к шагу 2, то есть решаем задачу
F (X *(1,6), 1,6)= +0,8×(3 x 1-2 x 2-5)2 ® min (4.3.5)
Ниже в таблице приведены результаты вычислений. В таблице применяются следующие сокращённые обозначения: Ñ Fk =Ñ F (Xk; 1,6), Fk = F (Xk; 1,6), D Fk = F (Xk +1; 1,6)- F (Xk; 1,6), rk +1= r (Xk +1, Xk).
| k | Xk | Ñ Fk | |Ñ Fk | | Xk +1 | Fk +1 | D Fk | rk +1 | Pk +1 |
| (0,6847; -0,2523) | (-8,9794; 5,9738) | 10,6864 | (1,5826; -0,8317) | 9,3696 | 9,3696>0 | h 0=0,05 | ||
| (1,1337; -0,542) | 3,9576 | -2,0026 | 0,5343 | |||||
| (1,1337; -0,542) | (2,0633; -2,6883) | 3,3888 | (1,0305; -0,4076) | 3,7446 | -0,2131 | 0,1694 | 1,1212 | |
| (1,0305; -0,4076) | (-1,1258; 0,2378) | 1,1507 | (1,087; -0,4195) | 3,7151 | -0,0296 | 0,0575 | 0,9562 |
Таким образом, X *(1,6)=(1,087; -0,4195) - решение задачи (4.3.5). При этом P (X *(1,6), 1,6)=0,9562>0,1. Полагаем r 3= C × r 2=4×1,6=6,4, X 0= X *(1,6)= =(1,087; -0,4195), и переходим к шагу 2 - решаем задачу
F (X *(6,4), 6,4)= +3,2×(3 x 1-2 x 2-5)2 ® min. (4.3.6)
Решение получается за одну итерацию: X *(6,4)=(1,0856; -0,3957). При этом P (X *(6,4), 6,4)=0,648>0,1.
Шаг 4. Так как P (X *(6,4), 6,4)=0,648>0,1, то полагаем r 4= C × r 3=4×6,4=25,4, X 0= X *(6,4)=(1,0856; -0,3957), и переходим к шагу 2 - решаем задачу
F (X *(6,4), 6,4)= +12,8×(3 x 1-2 x 2-5)2 ® min (4.3.7)
| k | Xk | Ñ Fk | |Ñ Fk | | Xk +1 | Fk +1 | D Fk | rk +1 | Pk +1 |
| (1,0856; -0,3957) | (-68,7558; 45,5666) | 82,4844 | (4,5234; -2,674) | 2549,104 | 2534, 525>0 | h 0=0,025 | ||
| (2,8045; -1,5349) | 536,1644 | 548, 5852>0 | h 0=0,01 | |||||
| (1,7732; -0,8514) | 61,5308 | 46,9516>0 | h 0=0,005 | |||||
| (1,7294; -0,6235) | 9,3079 | -5,2713 | 0,4124 | |||||
| (1,4294; -0,6235) | (42,821; -32,3902) | 56,9327 | (1,1953; -0,4616) | 6,7956 | -2,5122 | 0,2847 | ||
| (1,1953; -0,4616) | (-32,9199; 21,4413) | 39,2868 | (1,3599; -0,5688) | 5,5973 | -1,1971 | 0,1964 | ||
| (1,3599; -0,5688) | (22,1282; -15,6762) | 27,1183 | (1,2493; -0,4904) | 5,0261 | -0,5711 | 0,1356 | ||
| (1,2493; -0,4904) | (-15,8386; 9,9674) | 18,7139 | (1,3285; -0,5402) | 4,7529 | -0,2727 | 0,0936 | ||
| (1,3285; -0,5402) | (10,3751; -7,6957) | 12,9177 | (1,2766; -0,5017) | 4,6221 | -0,1306 | 0,0646 | ||
| (1,2799; -0,5017) | (-7,7038; 4,5266) | 8,9353 | (1,3151; -0,5243) | 4,5592 | -0,0631 | 0,0447 | 0,3561 | |
| (1,3151; -0,5243) | (4,7919; -3,8821) | 6,1671 | (1,2911; -0,5049) | 4,5284 | -0,0307 | 0,0308 | 0,0005 |
На последних двух шагах получаем r (Xk +1, Xk)<0,1 и | f (Xk +1)- f (Xk)|<0,1, а в последнем шаге - P (X *(25,4), 25,4)=0,0005<0,1. Процесс поиска закончен.
Ответ: точкой условного локального минимума является точка X *=(1,2911; -0,5049), f (X *)=4,5284 - условный локальный минимум.