Комплексные числа.
Выполненные задания присылать на почту alla.kurbatova2014@yandex.ru
Понятие комплексного числа.
Комплексным числом z называется выражение вида z = x +iy, где х и у – действительные числа, а i – так называемая мнимая единица, i 2= –1.
Если х = 0, то число 0 +iy = iy называется чисто мнимым; если у = 0, то число x +i 0 = х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т.е. RÌС.
Число х – действительная часть комплексного числа z и обозначается х= Rе z, а у – мнимой частью z, у =Im z.
Два комплексных числа z 1= x 1 +iy 1 z 2= x 2 +iy 2 называются равными тогда и только тогда, когда равны их действительные и мнимые части. Понятия больше и меньше для комплексных чисел не вводятся. Два комплексных числа, отличающиеся лишь знаком мнимой части, называются сопряжёнными.
|
|
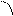
|
|
|




 Всякое комплексное число можно изобразить точкой М (х, у) плоскости Оху такой, что х= Rе z, у =Im z. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью.
Всякое комплексное число можно изобразить точкой М (х, у) плоскости Оху такой, что х= Rе z, у =Im z. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью.
Ось абсцисс – действительная ось, ось ординат – мнимая. Комплексное число можно задать в виде радиус вектора 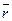 =
= 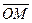 . Длина вектора
. Длина вектора 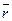 называется модулем этого числа и обозначается
называется модулем этого числа и обозначается 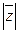 или r.
или r.
Величина угла между положительным направлением действительной оси и вектором 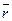 , изображающим комплексное число – аргумент этого числа, обозначается Arg z или
, изображающим комплексное число – аргумент этого числа, обозначается Arg z или 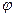 . Аргумент комплексного числа z =0 не определён. Аргумент комплексного числа z
. Аргумент комплексного числа z =0 не определён. Аргумент комплексного числа z 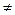 0 – величина многозначная и определяется с точностью до слагаемого
0 – величина многозначная и определяется с точностью до слагаемого 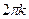 (k =0,–1,1,–2,2,…): Arg z= аrg z +
(k =0,–1,1,–2,2,…): Arg z= аrg z + 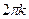 , где аrg z – главное значение аргумента, заключённое в промежутке
, где аrg z – главное значение аргумента, заключённое в промежутке 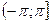 , т.е.
, т.е. 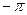 < аrg z £
< аrg z £ 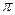 (иногда в качестве главного аргумента берут величину из промежутка
(иногда в качестве главного аргумента берут величину из промежутка 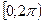 ).
).
Формы записи комплексных чисел.
Запись числа в виде 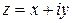 называют алгебраической формой комплексного числа. Модуль r и аргумент
называют алгебраической формой комплексного числа. Модуль r и аргумент 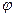 можно рассматривать как полярные координаты вектора
можно рассматривать как полярные координаты вектора 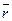 =
= 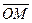 , изображающего комплексное число
, изображающего комплексное число 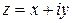 . Тогда получаем
. Тогда получаем 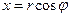 ,
, 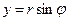 . Следовательно, комплексное число можно записать в виде
. Следовательно, комплексное число можно записать в виде 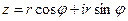 или
или 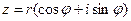 . Такая запись называется тригонометрической формой.
. Такая запись называется тригонометрической формой.
Модуль 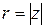 однозначно определяется по формуле
однозначно определяется по формуле 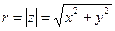 . Например,
. Например, 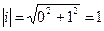 . Аргумент
. Аргумент 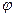 определяется из формул
определяется из формул
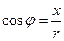 ,
, 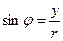 ,
, 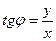
Так как 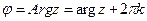 , то
, то  ,
, 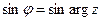 .
.
Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента z, т.е. считать 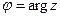 .
.
Так как 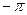 < аrg z £
< аrg z £ 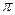 , то из формулы
, то из формулы 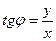 получаем, что
получаем, что
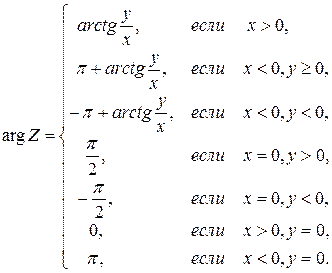
Используя формулу Эйлера 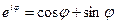 , комплексное число
, комплексное число 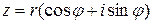 можно записать в показательной (или экспотенциальной) форме
можно записать в показательной (или экспотенциальной) форме 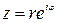 , где
, где 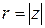 – модуль комплексного числа, а угол
– модуль комплексного числа, а угол 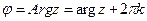 .
.
В силу формулы Эйлера функция 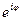 – периодическая с основным периодом 2p. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т.е. считать
– периодическая с основным периодом 2p. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т.е. считать 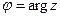 .
.
Пример 1: Записать комплексные числа z 1 = –1+ i и z 2 = –1в тригонометрической и показательной формах.
Решение: Для числа z 1 имеем:
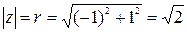
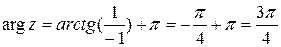 , т.е.
, т.е. 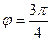 .
.
Поэтому 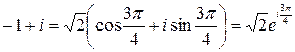
Для z 2 имеем 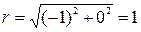
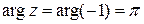 т.е.
т.е. 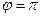 .
.
Поэтому 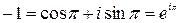 .
.
Действия над комплексными числами.


 Суммой двух комплексных чисел z 1 и z 2 у z1+z2
Суммой двух комплексных чисел z 1 и z 2 у z1+z2
 называется комплексное число, определяемое z 2
называется комплексное число, определяемое z 2

 равенством
равенством 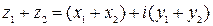 . z 1
. z 1
O x
|
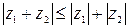 . Это соответствие называют неравенством треугольника.
. Это соответствие называют неравенством треугольника.
|
|
|




 Разностью двух комплексных чисел z 1 и z 2называется комплексное число z, которое будучи сложенным с z 2, даёт число z 1, т.е. z = z 1 – z 2, если
Разностью двух комплексных чисел z 1 и z 2называется комплексное число z, которое будучи сложенным с z 2, даёт число z 1, т.е. z = z 1 – z 2, если 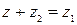 .
.
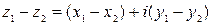 .
.
Из равенства следует, что геометрически комплексные числа вычитаются как векторы. Из рисунка видно, что 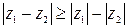 .
.
Отметим, что 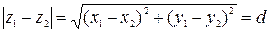 , т.е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.
, т.е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.
Поэтому, например, равенство 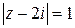 определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки
определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки 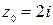 , т.е. окружность с центром в
, т.е. окружность с центром в 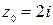 и радиусом 1.
и радиусом 1.
Произведением комплексных чисел z 1= x 1 +iy 1 и z 2= x 2 +iy 2 называется комплексное число, определяемое равенством:
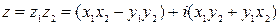
Произведение комплексных чисел можно находить путём формального перемножения двучленов x 1 +iy 1 и x 2 +iy 2, учитывая, что i 2= –1.
Например, (2–3 i)(–5+4 i)= –10+8 i +15 i –12 i 2 = –10+23 i +12=2+23 i.
Заметим, что 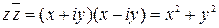 – действительное число.
– действительное число.
Умножение комплексных чисел обладает переместительным, сочетательным и распределительным свойствами.
Найдём произведение комплексных чисел, заданных в тригонометрической форме: 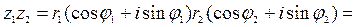
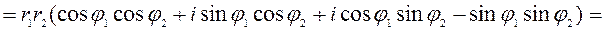
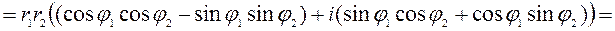
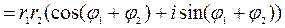
Мы показали, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. В частности
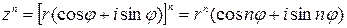 – формула Муавра.
– формула Муавра.
Пример 2: Найти 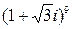
Решение: Запишем сначала число 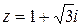 в тригонометрической форме:
в тригонометрической форме:
 ;
; 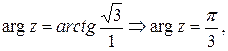
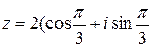
По формуле Муавра имеем
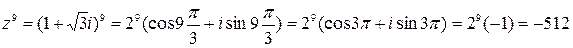
Частным двух комплексных чисел z 1и z 2≠0 называется комплексное число z, которое, будучи умноженным на z 2, даёт число z 1, т.е. 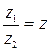 , если
, если 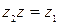 .
.
Если положить 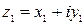 ,
, 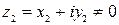 ,
, 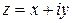 , то из равенства
, то из равенства 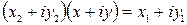 следует
следует
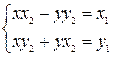
Решая систему, найдём значения х и у:
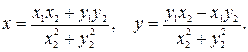
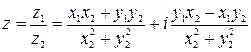 .
.
На практике частное двух комплексных чисел находят путём умножения числителя и знаменателя на число, сопряжённое знаменателю.
Пример 3: Выполнить деление 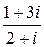
Решение: 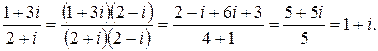
Для тригонометрической формы комплексного числа деление имеет вид: 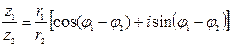 ,
,
т.е. 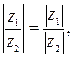
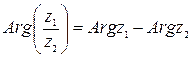 .
.
Корнем п-ой степени из комплексного числа z называется комплексное число 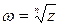 , удовлетворяющее равенству
, удовлетворяющее равенству 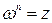 .
.
Если положить 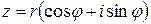 , а
, а 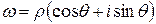 , то по определению корня и формуле Муавра, получаем
, то по определению корня и формуле Муавра, получаем
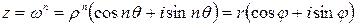 .
.
Отсюда имеем 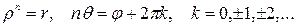
Т.е. 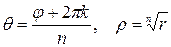 (арифметический корень).
(арифметический корень).
Поэтому корень п -ой степени из комплексного числа имеет п различных значений, которые находятся по формуле:
 ,
, 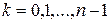
Точки, соответствующие значениям 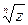 , являются вершинами правильного п -угольника, вписанного в окружность радиуса
, являются вершинами правильного п -угольника, вписанного в окружность радиуса 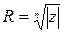 с центром в начале координат.
с центром в начале координат.
Пример 4: Найти все значения 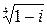 .
.
Решение: Запишем комплексное число 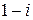 в тригонометрической форме.
в тригонометрической форме.
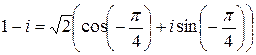 .
.
 .
.
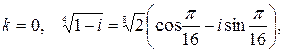
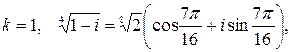
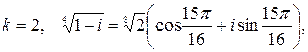
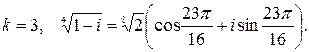
Пример 5: Какое множество точек на комплексной плоскости определяется условием 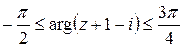 ?
?

|

 Решение: Комплексное число
Решение: Комплексное число 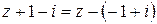 изображается вектором, началом которого является точка
изображается вектором, началом которого является точка 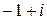 , а концом ‒ точка z. Угол между этим вектором и осью ОХ есть
, а концом ‒ точка z. Угол между этим вектором и осью ОХ есть 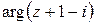 , и он меняется в пределах от
, и он меняется в пределах от 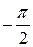 до
до 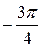 .
.

|
|

 Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки
Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки 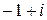 и образующими с осью ОХ углы в
и образующими с осью ОХ углы в 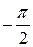 и
и 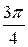 рад.
рад.