Границы раздела моделируемых сред могут быть с достаточной степенью точности аппроксимированны координатными поверхностями какой-либо ортогональной криволинейной системы координат. Поэтому при решении прямых задач геоэлектроразведки важно выбрать подходящую ортогональной криволинейной системы координат (q_1,q_2,q_3) и представить задачу в новых переменных.
В методах современной матфизики находят применение около 30 таких систем. Рассмотрим основные.
Декартова система координат
Координатными поверхностями данной системы являются плоскости. Основные модели сред - однородное пространство, полупространство, плоско-параллельные оризонтально-слоистые и вертикально-слоистые пространство и полупространство.
Цилиндрическая система координат
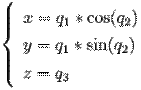
Сферическая система координат
Плоскости q_3=const, концентрические сферы q_1=const и конусы q_2=const составляют три семейства координатных поверхностей данной системы.
Параболическая цилиндрическая система координат
Координатные поверхности q_1=const и q_2=const образуют взаимоортогональные семейства араболических цилиндров, а q_3=const - есть плоскости.
Эллиптическая цилиндрическая система координат
Поверхности: софокусные эллиптические цилиндры q_1=const, гиперболические цилиндры q_2=const и плоскости q_3=const
Коническая система координат
Поверхности q_1=const, q_2=const образуют взаимоортогональные семейства параболоидов, a q_3=const - есть плоскости
Параболическая система координат вращения
Поверхности q_1=const, q_2=const образуют взаимоортогональные семейства параболоидов, a q_3=const - есть плоскости
Формулы перевода
Пусть новая ортогональной криволинейной системы координат (q 1, q 2, q 3) связана с декартовой (x,y,z) уравнениями
В новых координатах электрический потенциал описывается следующей краевой задачей
Оператор Лапласа:
(1.15) 
(1.16)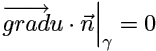 
(1.17) 
(1.18) 
где Hj, j = 1..3 – коэффициенты Ламэ
(1.19) 
(1.20) 
- еденичные векторы, направленные по касательным к поверхностям qj = const в точке в сторону возрастания переменных qj.
Пример
Оператор Лапласа в цилиндрическое системе координат.
Задание (домашнее)
Оператор Лапласа - в сферическую систему координат.
Метод интегральных представлений решения прямых задач геоэлектрики
Данный метод формируется на основе интегральной формулы Грина с построением функции Грина вмещающего пространства. Он является универсальным методом понижения геометрической сложности исследуемой среды. С другой стороны этот метод может быть использован также для поэтапного усложнения геометрии модели.
Идея метода
Рассмотрим кусочно-однородную среду 
, состоящую из областей 
. Пусть в среде 
в точке с координатами 
находится точечный источник постоянного электрического тока интенсивности I (рис. 2).
Рис. 2.:Кусочно-однородная среда
Математическая модель распределения потенциального поля в данной среде описывается следующей краевой задачей эллиптического типа:
, (2.1.1)
; (2.1.2)
; (2.1.3)
, 
; (2.1.4)
;
(2.1.5)
Здесь 
– граница области 
, 
– номера областей, участки границ которых являются частью границы «земля/воздух» – 
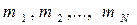– номера областей с участками границ, уходящими в бесконечность, 
– вектор внешней нормали.
Рассмотрим вспомогательную функцию Грина 
– функцию точечного источника в среде без включений (во вмещающем пространстве).
– источник тока;
– приёмник тока;
(2.1.6)
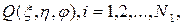
(2.1.7)
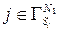(2.1.8)
(2.1.9)
Краевая задача (2.1.6)–(2.1.9) определяет функцию Грина в полупространстве для уравнения эллиптического типа с кусочно-постоянными коэффициентами. Будем считать, что функция Грина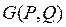 
определяется в среде, состоящей из первых 
областей 
.
Если = 
, то при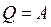 
решение задачи (2.1.1)–(2.1.5) имеет вид:
.
Если < , то рассмотрим для каждой области , 
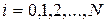формулу Грина:
(2.1.10)
Подставив в (2.1.10) вместо функции 
функцию Грина 
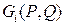, определяемую решением граничной задачи (2.1.6)–(2.1.9), получим обобщенное интегральное представление решения краевой задачи (2.1.1)–(2.1.5) в области 
, 
:
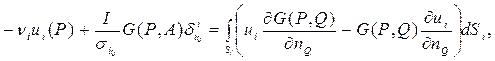(2.1.11)
где 
– символ Кронекера: 
.
Умножив (2.1.11) на 
и просуммировав результат по 
от 0 до N, получим:
С учетом граничных условий (2.1.2)–(2.1.5) и (2.1.7)–(2.1.9) и в силу непрерывности функции 
получим более простое интегральное представление решения задачи (2.1.1)–(2.1.5):
, (2.1.12)
где 
– множество номеров таких областей, которые имеют участки границ, соприкасающихся с границей области 
, то есть пересечение границ не пусто.
Согласно формуле (2.1.12), решение задачи может быть получено в любой точке исходной кусочно-однородной среды, если определено решение задачи (2.1.6)–(2.1.9), то есть функция Грина 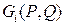, и известны граничные значения потенциала на границах сред, не вошедших в задачу для функции Грина.
Полагая в (2.1.12), что точка Р принадлежит каждой из поверхностей 
получим систему линейных интегральных уравнений Фредгольма второго рода относительно неизвестных граничных значений потенциала 
вида: 
, 
, 
, 
, 
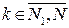, (2.1.13)
где 
.
Универсальность метода интегральных представлений позволяет варьировать вмещающее пространство от однородного до исходного сложно построенного.
Этот подход допускает реализацию процедуры упрощения геометрии среды (задача для функции Грина аналогична исходной задаче, но с меньшим числом областей). Однако данный метод позволяет и усложнять геометрию пространства, так как кусочно-однородное пространство, для которого получено решение прямой задачи, может быть принято за вмещающее пространство более сложной среды (то есть модель может быть дополнена новым включением). К новой задаче применимы аналогичные формулы.
Методом интегральных преобразований могут быть решены задачи для всех основных типов геологических разрезов, осложненных наличием включений: однородного пространства и полупространства, горизонтально-вертикально и цилиндрически-слоистых сред, клиновидных сред, пространств с различными видами поднятий, в сферических и сфероидально- неоднородных средах.
|
| Геоэлектрический разрез |
Применение метода
Постановка задачи
В декартовой системе координат построим математическую модель поля постоянного электрического тока силы I точечного источника, находящегося в точке 
, считая, что удельная электрическая проводимость — есть кусочно-постоянная функция, границы сред — гладкие.
(1) 
;
(2) 
;
Контакт с непроницаемой средой:
(3) 
;
Условие непрерывности потенциала и плотности тока:
(4) 
(5) 
(6) 