Содержание
Введение
. Понятие функции двух переменных
. Предел и непрерывность функции двух переменных
. Частные производные первого порядка. Полный дифференциал
. Частные производные высших порядков
. Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
. Условный экстремум
Заключение
Список литературы
предел функция производная дифференциал экстремум
Введение
Явления, происходящие в общественной жизни, природе, экономике, не всегда можно описать с помощью функции всего лишь одной переменной.
Например, рентабельность предприятия зависит от прибыли, основных и оборотных фондов. Понятие функции нескольких переменных появилось именно для изучения такого рода зависимостей.
В наше время наука неумолимо быстро развивается, и для ее развития требуются все более сложные решения тех или иных вопросов. Поэтому для роста научно технического прогресса и усложнения экономических процессов требуются новые привлечения математических процессов.
В данной работе рассмотрим функции двух переменных, так как все основные понятия и теоремы, сформулированные для функций двух переменных, легко обобщаются на случай большего числа переменных.
Понятие функции двух переменных
Многие явления, происходящие в природе, экономике, общественной жизни нельзя описать с помощью функции одной переменной. Например, рентабельность предприятия зависит от прибыли, основных и оборотных фондов. Для изучения такого рода зависимостей и вводится понятие функции нескольких переменных.
В данной лекции рассматриваются функции двух переменных, так как все основные понятия и теоремы, сформулированные для функций двух переменных, легко обобщаются на случай большего числа переменных.
Пусть 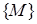 - множество упорядоченных пар действительных чисел
- множество упорядоченных пар действительных чисел  .
.
Определение 1. Если каждой упорядоченной паре чисел  по некоторому закону
по некоторому закону  поставлено в соответствие единственное действительное число
поставлено в соответствие единственное действительное число  , то говорят, что задана функция двух переменных
, то говорят, что задана функция двух переменных 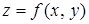 или
или  . Числа
. Числа  называются при этом независимыми переменными или аргументами функции, а число
называются при этом независимыми переменными или аргументами функции, а число  - зависимой переменной.
- зависимой переменной.
Например, формула  , выражающая объем цилиндра, является функцией двух переменных:
, выражающая объем цилиндра, является функцией двух переменных: 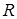 - радиуса основания и
- радиуса основания и 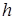 - высоты.
- высоты.
Пару чисел  иногда называют точкой
иногда называют точкой 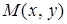 , а функцию двух переменных - функцией точки
, а функцию двух переменных - функцией точки 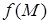 .
.
Значение функции 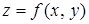 в точке
в точке 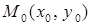 обозначают
обозначают  или
или  и называют частным значением функции двух переменных.
и называют частным значением функции двух переменных.
Совокупность всех точек 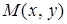 , в которых определена функция
, в которых определена функция 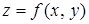 , называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями.
, называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями.
Например, область определения функции 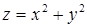 - вся плоскость, а функции
- вся плоскость, а функции  - единичный круг с центром в начале координат (
- единичный круг с центром в начале координат ( или
или 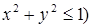 .
.
Предел и непрерывность функции двух переменных
Понятия предела и непрерывности функции двух переменных аналогичны случаю одной переменной.
Пусть 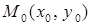 - произвольная точка плоскости.
- произвольная точка плоскости. 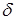 - окрестностью точки
- окрестностью точки 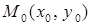 называется множество всех точек
называется множество всех точек 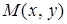 , координаты которых удовлетворяют неравенству
, координаты которых удовлетворяют неравенству  . Другими словами,
. Другими словами, 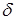 - окрестность точки
- окрестность точки 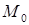 - это все внутренние точки круга с центром в точке
- это все внутренние точки круга с центром в точке  и радиусом
и радиусом 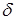 .
.
Определение 2. Число  называется пределом функции
называется пределом функции 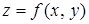 при
при 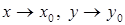 (или в точке
(или в точке 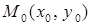 ), если для любого сколь угодно малого положительного числа
), если для любого сколь угодно малого положительного числа  существует
существует 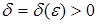 (зависящее от
(зависящее от 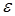 ) такое, что для всех
) такое, что для всех  и удовлетворяющих неравенству
и удовлетворяющих неравенству  выполняется неравенство
выполняется неравенство 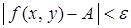 .
.
Обозначается предел следующим образом:
 или
или  .
.
Пример 1. Найти предел  .
.
Решение. Введем обозначение  , откуда
, откуда  . При
. При 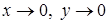 имеем, что
имеем, что 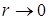 . Тогда
. Тогда
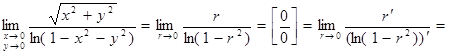
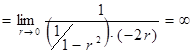 .
.
Определение 3. Функция 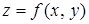 называется непрерывной в точке
называется непрерывной в точке 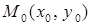 , если: 1)
, если: 1) 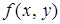 определена в точке
определена в точке 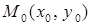 и ее окрестности; 2) имеет конечный предел
и ее окрестности; 2) имеет конечный предел 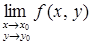 ; 3) этот предел равен значению функции в точке
; 3) этот предел равен значению функции в точке 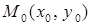 , т.е.
, т.е.  .
.
Функция 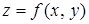 называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
Точки, в которых условие непрерывности не выполняется, называются точками разрыва этой функции. В некоторых функциях точки разрыва образуют целые линии разрыва. Например, функция  имеет две линии разрыва: ось
имеет две линии разрыва: ось  (
( ) и ось
) и ось 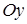 (
(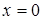 ).
).
Пример 2. Найти точки разрыва функции 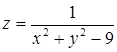 .
.
Решение. Данная функция не определена в тех точках, в которых знаменатель обращается в нуль, т. е. в точках, где  или
или 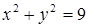 . Это окружность с центром в начале координат и радиусом
. Это окружность с центром в начале координат и радиусом  . Значит, линией разрыва исходной функции будет окружность
. Значит, линией разрыва исходной функции будет окружность 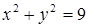 .
.