Модели временных рядов, которые сочетают авторегрессионный процесс с моделью скользящей средней называются авторегрессионными моделями скользящей средней (АРСС, ARMA). Модель АРСС(p,q) имеет р временных лагов в авторегрессионном процессе и q интервалов в модели скользящей средней.
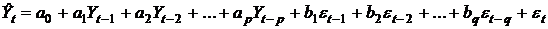(5)
где 
- остаточный член ошибки.
Так АРСС(3,2) имеет вид:
Идентификация модели АРСС.
Опр.8. Пусть дана модель АРСС(p, q) для временного ряда Yt. Идентификацией этой модели называется процедура определения неизвестных значений p и q.
Существует несколько подходов к идентификации моделей АРСС.
I подход:
Идентификацию модели АРСС проводят на визуальном анализе коррелограммы АКФ и частичной коррелограммы ЧАКФ. Здесь используются следующие особенности АКФ:
§ В случае АР моделей ее модуль убывает по экспоненте, осциллируя около нуля;
- В случае СС(q) модели только первые q значений отличны от нуля;
- В модели АРСС(p, q), после q-р значений, АКФ имеет вид, такой же, как АР модель.
Свойства поведения ЧАКФ:
§ Для АР(р) моделей, она равна нулю после первых р значений.
§ Для моделей СС она экспоненциально убывает по модулю.
§ Для АРСС(р,q) моделей, после первых р-q значений,она ведет себя также как и для модели СС.
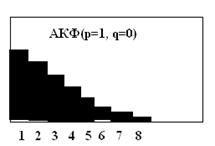
АРСС(1, 0)
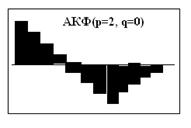
АРСС(2, 0)
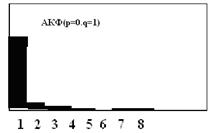
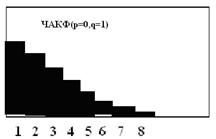
АРСС(0, 1)
АРСС(0, 2)
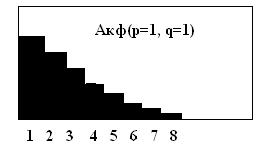
АРСС(1, 1)
Отметим, что метод идентификации моделей АРСС, используя коррелограммы АКФ и ЧАКФ, не является строгим.
II подход:
Проверка значимости коэффициентов автокорреляции проводится при помощи критерия стандартной ошибки и Q-критерия Бокса-Пирса.
Критерий стандартной ошибки.
При этом критерии коэффициенты автокорреляции проверяются для каждого лага, для этого рассчитываются стандартные ошибки следующим образом: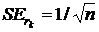 
, где k – порядок лага. (6)
|
|
Коэффициенты автокорреляции случайных данных обладают выборочным распределением, приближающимся к нормальному с нулевым математическим ожиданием и средним квадратическим отклонением, равным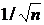 
.
Q-критерий Бокса-Пирса.
При этом критерии, на значимость проверяют все множество коэффициентов автокорреляции как группу. Рассчитывают Q расч как:
, (7)
где m – максимальный рассматриваемый лаг,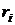 
- коэффициенты автокорреляции. Из таблицы 
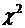критических значений находится 
для m степеней свободы. Затем сравнивают Q расч и , если Q расч> 
, то порядок авторегрессионного процесса равен m.
III подход:
Для проверки автокорреляции в рядах, где присутствуют элементы авторегрессии и скользящей средней, используется критерий Люнга-Бокса.
Значение LB расч определяется по формуле:
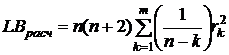(8)
где m – максимальное число временных лагов, рассматриваемых в модели, р – порядок авторегрессии, q – порядок процесса скользящей средней, n –число наблюдений во временном ряду, r2k – коэффициент автокорреляции.
Из таблицы 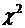критических значений находится 
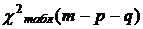для m-p-q степеней свободы. Затем сравнивают LB расч и 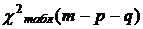, если LBрасч> 
, то порядок авторегрессионного процесса равен p, а порядок процесса скользящей средней - q.