Арифметические операции над степенными рядами.
1) Интегрирование степенных рядов.
Если некоторая функция
f(x) определяется - степенным рядом, то интеграл от этой функции можно записать в виде ряда:
2) Дифференцирование степенных рядов.Производная функции, которая определяется степенным рядом, находится по формуле:
3) Сложение, вычитание, умножение и деление степенных рядов. Сложение и вычитание степенных рядов сводится к соответствующим операциям с их членами:
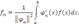Произведение двух степенных рядов выражается формулой: 
Коэффициенты сi находятся по формуле:
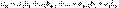
Деление двух степенных рядов выражается формулой:
Для определения коэффициентов
qn рассматриваем произведение
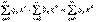, полученное из записанного выше равенства и решаем систему уравнений:
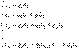
9. Разложение функций в степенные ряды Пусть дана функция f (x), которую требуется разложить в степенной ряд, т.е. представить в виде 
(30): Задача состоит в определении коэффициентов 
ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:
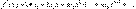
(31) 
Полагая в равенствах (30) и (31) х = 0, находим 
Тогда 
Подставляя найденные выражения в равенство (30), получим 
(32)
Это разложение функции f (x) в ряд называется рядом Маклорена.
Ряды Тейлора и Маклорена
Если ф-я f(x) имеет непрерывные производные вплоть до(n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
+ 
где Rn − остаточный член в форме Лагранжа определяется выражением
Если приведенное разложение сходится в некотором интервале x, т.е. 
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена:
Примеры: ☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺
● 
● 
10. Приближённое вычисление значений функций. Идея таких вычислений простая. Пусть известно значение функции в точке x0, и функция разлагается в окрестности точки x0 в ряд Тейлора. Тогда значение функции в точке x1, которое надо найти, равно:
,и принимается
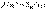. Естественно, мы должны гарантировать, что погрешность такого приближения не превышает заданной величины 
. Погрешность равна остатку ряда после n-го члена (или остаточному члену формулы Тейлора), поэтому необходимо строить оценку сверху для 
(или 
). При оценке 
принципиально отличны два случая. Если остаток - знакочередующийся ряд, то 
просто оценивается по своему первому члену. Если остаток не является знакочередующимся рядом, то необходимо оценивать всю его сумму. Обычно в этом случае остаток мажорируют сходящейся геометрической прогрессией.
Вычисление интегралов. Подынтегральную функцию представляют в виде ряда Тейлора и почленно интегрируют. Пример: Вычислить J = 
с точностью 0,001.J = 
dx 1/x (x – x3/3! + x5/5! –..) = (x – x3/3!3 + x5/5!5 -..) |0.50 = 1/2 –1/ 233!3 + ½55!5 -.Имеем 1/ 233!3 = 1/144 > 0.001, ½55!5 = 1/19200 < 0.001. Ряд знакочередующийся и по признаку Лейбница погрешность 
не превосходит модуля первого из отброшенных членов, т.е. точность 0,001 обеспечивают два первых члена ряда J = 1 + 1/144 = 0.4931
11. Периоди́ческая фу́нкция ― такая функция f(x), для которой существует положительное число T>0, такое что на всей области определения функции выполняется равенство f(x)=f(x+T). Наименьшее из этих чисел называется периодом функции. Интеграл от периодической функции. Если f(x) является периодической интегрируемой функцией с периодом T, то 
при любом a, 
< a < 
.Действительно, 
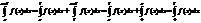
так как, в силу периодичности,
, где x' = x-T. Таким образом, интеграл от периодической функции с периодом T по любому отрезку длины T имеет одно и то же значение. Отправляясь от непереодической функции f(x), заданной на отрезке a<=x<=a+T, можно построить периодическую функцию F(x) с периодом T, совпадающую с f(x) на отрезке a<=x<=a+T. Если рассуждать геометрически, то для этого нужно выполнить переносы графика функции f(x) параллельно оси x вправо и влево на расстоянии T,2T,3T……nT,. Этот процесс назовем периодическим продолжением функции f(x) за пределы отрезка a<=x<=a+T с периодом T. Основная тригонометрическая система является ортогональной на отрезке [-l, l] в следующем смысле: интеграл по отрезку [-l, l] от произведения любых двух различных функций этой системы равен нулю, а интеграл по отрезку [-l, l] от квадрата любой функции этой системы отличен от нуля. Пусть некоторая функция f (x) представлена в виде разложения по полному набору функций, ортогональных на промежутке
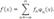(a, b):
(1)
Составим скалярное произведение функций и f(x) на этом промежутке: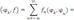 
(2)
Тогда (3). Если функции нормированы на единицу, то 
(4)
Ряд (1), в котором коэффициенты fn определяются формулой (3), называется обобщенным рядом Фурье, а числа fn – коэффициентами Фурье. Ряд Фурь е — представление произвольной функции с периодом в виде ряда
12. Пусть f(x) – четная функция, определенная и интегрируемая на симметричном промежутке 
. Тогда 
Интеграл от четной функции сводится к двойному интегралу от половины симметричного промежутка 
Пусть f(x) – нечетная функция, определенная и интегрируемая на симметричном промежутке 
. Тогда
Интеграл от нечетной функции по симметричному промежутку равен нулю: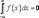 
13. и 14. Не сделал жульшпед