Сформулируйте основное уравнение динамики вращательного движения и дайте определение всем величинам, входящим в уравнение.
. (4.8)
Угловое ускорение, приобретаемое твердым телом, прямо пропорционально результирующему моменту всех действующих на тело внешних сил и обратно пропорционально моменту инерции тела.
Для описания вращательного движения твердого тела вводят понятие момента силы 
относительно неподвижной точки. Это векторная величина, равная векторному произведению радиус-вектора 
, проведенного из начала координат в точку приложения силы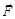 
, и силы :
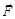. (4.6)
Модуль момента силы
Мерой инертности тела при вращательном движении служит момент инерции J. Это скалярная величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний ri до оси вращения:
. (4.4)
В случае непрерывного распределения масс эта сумма сводится к интегралу:
,
быстрота изменения вектора угловой скорости характеризуется угловым ускорением 
:
Выведите рабочую формулу (4.15).
, (4.9)
где: а – ускорение падающего груза, r = d/ 2 – радиус шкива.
В свою очередь, пользуясь известным выражением для равноускоренного движения груза:
, (4.10)
(h – высота падения груза, t – время падения груза) находим:
, (4.11)
или, используя (4.9):
. (4.12)
Момент силы, приложенной к маятнику, находим по формуле (4.7), где: F – сила, действующая на шкив. Но 
, и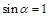 
. Тогда формула (4.7) имеет вид: 
.
Силу F можно найти из уравнения движения груза:
, (4.13)
где: m – масса падающего груза, а 
, 
– сила натяжения нити. Тогда для момента силы получим следующее выражение:
. (4.14)
Используя формулу (4.8) получим:
. (4.15)
3. Укажите основные источники погрешностей измерений. Выведите формулу для расчета погрешности J.
|
|
4. Какую роль играет момент инерции тела при его вращательном движении? Объясните физический смысл момента инерции.
Во вращательном движении большое значение имеет физическая величина, называемая моментом инерции тела. Эта величина играет такую же роль, как и масса при поступательном движении. Другими словами, момент инерции тела является мерой его инертности во вращательном движении, т.е. характеризует способность тела сохранять угловую скорость.
5. От чего зависит момент инерции маятника Обербека (формула (4.16))?
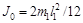
где: m 0 = 0,114 кг – масса подвижного груза крестовины; R – расстояние от центра масс подвижного груза до оси вращения; r 0= 0,015 м – радиус груза; l = 0,02 м – длина образующей груза. Момент инерции системы без грузов J 0 можно определить по формуле:
6.Выведите формулу для расчета момента инерции цилиндра или стержня.
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
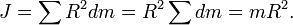
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R 1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
|
|
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Тонкий стержень (ось проходит через центр)
Вывод формулы [скрыть]
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы [скрыть]
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l /2. По теореме Штейнера новый момент инерции будет равен
7. Сформулируйте теорему Штейнера и приведите примеры ее применения.
момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
где
JC — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m — масса тела,
d — расстояние между указанными осями.