Исследование распределения температуры в тонком цилиндрическом стержне
Курсовая работа по информатике
Исполнитель: Солнцев П.В.
Санкт-Петербургский Государственный Технологический Институт (Технический Университет)
Санкт-Петербург 2001
Введение
В решении любой прикладной задачи можно выделить три основных этапа: построение математической модели исследуемого объекта, выбор способа и алгоритма решения полученной модели, численная реализация алгоритма.
Цель данной работы – на примере исследования распределения температуры в тонком цилиндрическом стержне освоить основные методы приближённых вычислений, приобрести практические навыки самостоятельных исследований, существенно опирающихся на использование методов прикладной математики.
Постановка задачи
Физическая модель
В ряде практических задач возникает необходимость исследования распределения температуры вдоль тонкого цилиндрического стержня, помещённого в высокотемпературный поток жидкости или газа. Это исследование может проводиться либо на основе обработки эксперимента (измерение температуры в различных точках стержня), либо путём анализа соответствующей математической модели.
В настоящей работе используются оба подхода.
Тонкий цилиндрический стержень помещён в тепловой поток с постоянной температурой , на концах стержня поддерживается постоянная температура 0.
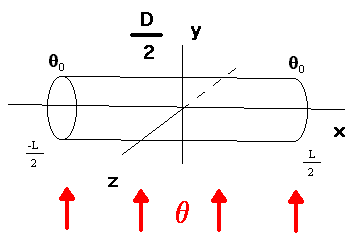
1.2 Математическая модель
Совместим координатную ось абсцисс с продольной осью стержня с началом в середине стержня. Будем рассматривать задачу (распределения температуры по стержню) мосле момента установления режима Т0.
 |
Первая математическая модель использует экспериментальные данные, при этом измеряют температуру Ui стержня в нескольких точках стержня с координатами xi. Результаты измерения Ui рассматривают как функцию регрессии и получают статистики. Учитывая чётность U(x) можно искать её в виде многочлена по чётным степеням x (ограничимся 4-ой степенью этого многочлена).
 |
(1.1)
Задача сводится к отысканию оценок неизвестных параметров, т.е. коэффициентов a0, a1 и a2, например, методом наименьших квадратов.
Вторая математическая модель, также использующая экспериментальные данные, состоит в применении интерполяционных формул и может употребляться, если погрешность измерений температуры Ui пренебрежимо мала, т.е. можно считать, что U(xi)=Ui
 |
Третья математическая модель основана на использовании закона теплофизики. Можно доказать, что искомая функция U(x) имеет вид:
(1.2)
где коэффициент теплопроводности, коэффициент теплоотдачи, D – диаметр стержня, температура потока, в который помещён стержень.
 |
Ищем U(x) как решение краевой задачи для уравнения (1.2) с граничными условиями:
(1.3)
на отрезке [-L|/2;L/2], где L – длина стержня, постоянная температура, поддерживаемая на концах стержня.
Коэффициент теплопроводности зависит от температуры:
 |
(1.4)
где начальное значение коэффициента теплопроводности, вспомогательный коэффициент.
 |
Коэффициент теплоотдачи вычисляют по формуле:
(1.5)
 |  | ||
т.е. как среднее значение функции
за некоторый отрезок времени от 0 до Т, здесь значение при t стремящемся к бесконечности, b – известный коэффициент.
 |
Время Т0, по истечении которого распределение температуры в стержне можно считать установившимся определяется по формуле:
(1.6)
 |
где а – коэффициент температуропроводности, наименьший положительный корень уравнения:
(1.7)
Задание курсовой работы
Вариант № 136
Исходные данные:
L = 0.0386 м
D = 0,00386 м
оС
оС
141,85 (Вт/м*К)
2,703*10-4
6,789*10-7
3,383*102 (Вт/м2*К)
218 оС
А = 3,043*10-5 (м2/с)
| X, м | U, oC |
| 0,00386 | |
| 0,00772 | |
| 0,01158 | |
| 0,01544 | |
| 0,01930 |
Обработка результатов эксперимента.