Решение уравнения комбинированным методом

Время установления режима определяется по формулам (1.6) и (1.7).

Проведём сначала отделение корней. Имеем y = ctg(x) и y = Ax. Приведём уравнение к виду: A x sin(x)-cos(x) = 0. Проведём процесс отделения корня.

 

F(x)	-1	-0.6285	0.4843
x	0.01	0.05	0.1

т.е. с [0.01;0.05]

Убедимся, что корень действительно существует и является единственным на выбранном интервале изоляции.

f(a) f(b)<0 – условие существования корня выполняется

f’(x) на [a;b] – знакопостоянна: f’(x)>0 – условие единственности также выполняется. Проведём уточнение с погрешностью не превышающей ^

Строим касательные с того конца, где f(x) f”(x)>0

f”(x)=(2A+1)cos(x) – A x sin(x). f”(x)>0 на (a;b), следовательно касательные строим справа, а хорды слева. Приближение корня по методу касательных:

по методу хорд:

Вычисление ведём до того момента, пока не выполнится условие:

Результаты вычислений заносим в таблицу:

 

n	an	bn	f(an)	f(bn)
	0.05	0.1	-0.6285	0.4843
	0.07824	0.08366	-0.0908	0.0394
	0.08202	0.08207	-9.1515 10-4	3.7121 10-4
	0.08206	0.08206	-8.4666 10-8	3.4321 10-8

 

Т₀ = 72,7176 секунд.

4.2 Решение уравнения комбинированным методом

Приведём f(x) = 0 к виду x = (x). Для этого умножим обе части на произвольное число , неравное нулю, и добавим к обеим частям х:

X = x - f(x)

xx - A x sin(x) + cosx)

В качестве возьмём:

где М = max [f’(x)] на [a;b], а m = min [f’(x)] на [a’b]

В силу монотонности f’(x) на [a;b] имеем m = f’(а), М = f’(b). Тогда 0,045.

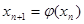Приближение к корню ищем по следующей схеме:

Вычисление ведём до тех пор, пока не выполнится условие:

(q = max |’(x)| на [a’b])

’(x) на [a’b] монотонно убывает, поэтому максимум его модуля достигается на одном из концов.

’(0,05) = 0,3322 ’(0,1) = -0,3322, следовательно, q = 0.3322 < 1. В этом случае выполняется условие сходимости и получается последовательность:

 

i	xi	(xi)	 xi
	0.075	0.082392	0.00739
	0.082392	0.082025	0.000367
	0.082025	0.08206	3.54 10-5
	0.08206	0.082057	3.33 10-6
	0.082057	0.082057	3.15 10-7

 

Итак, с погрешностью, меньшей 10^-4, имеем:

Т0 = 72,7176 с., 0.03142

 

5. Решение краевой задачи

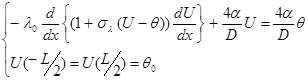Используем метод малого параметра. Краевую задачу запишем в виде:

(5.1)

Введя новую переменную y = (U - __, запишем (5.1) в виде:

(5.2)

__0.18L/2 =0.0193. В качестве малого параметра возьмём .

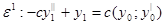Тогда, подставив y(x) в уравнение (5.2) и перегруппировав члены при одинаковых степенях , получим:

(5.3)

Ограничимся двумя первыми членами ряда:

Из (5.2) и (5.3) находим общее решение уравнения для y₀:

где y₀ с тильдой – частное решение данного неоднородного уравнения; y₍₁₎ и y₍₂₎ – линейно независимые решения однородного уравнения.

Корни уравнения:

y_0общ = 1 + c₁ch(px)+c₂sh(px), где p = 0.01953

Константы найдём из граничных условий:

откуда с₁ = 0, с₂ = -0,57; т.е. имеем функцию:

y₀ = 1 - 0.57 sh(px)

Общее решение:

Частное решение:

Дифференцируя и подставляя в уравнение, получим:

А₁ = 0; А₂ = -0,1083; В₁ = 0; В₂ = 17,1569;

Тогда общее решение для y₁ имеет вид:

с₃ = 0; с₄ = 0,0462

Перейдя к старой переменной U, получим:

____

Итоговое уравнение:

 

Пользуясь этой формулой, составим таблицу значений функции U(x):

x	U(x)	U
	352.9075
0.0019	350.4901
0.0039	343.1972
0.0058	330.9053
0.0077	313.4042
0.0097	290.391
0.0116	261.4598
0.0135	226.0893
0.0154
0.0174	133.2579
0.0193

Используя данную таблицу, строим график функции U(x).

[см. приложение 1]

Заключение

Решение задачи на ЭВМ при помощи вычислительной системы ManhCad 7.0 дало результаты (функцию распределения температуры в тонком цилиндрическом стержне), полученные по решению практического задания и обработкой эксперимента (функции регрессии), которые практически (в пределах погрешности) совпадают с экспериментальными значениями.

Список литературы

1. Методические указания «Методы приближённых вычислений. Решение нелинейных уравнений» (ЛТИ им. Ленсовета, Л. 1983)

2.Методические указания «Приближённые методы ислисления определённых интегралов» (ЛТИ им. Ленсовета, Л. 1986)

Методические указания «Изучение распределения температуры в тонком цилиндрическом стержне» (ЛТИ им. Ленсовета, Л. 1988)