Теплопроводность при нестационарном режиме

Процессы передачи теплоты, в которых температурное поле и поле теплового потока изменяются во времени, называются неста­ционарными.

Нестационарные тепловые процессы в технике и природе встре­чаются практически чаще, чем стационарные. Нагрев или охлажде­ние приборов и машин при пуске, останове или изменении режима; конструктивных элементов зданий и других сооружений при изме­нении наружной температуры; термическая обработка продуктов и изделий; работа регенеративных теплообменных аппаратов – все это примеры нестационарных тепловых процессов.

Длительность процессов нестационарного конвективного тепло­обмена и излучения сравнительно мала и не имеет существенного влияния на формирование температурных полей тел в нестационар­ном режиме, поэтому эти процессы пока мало изучены – их неста­ционарностью обычно пренебрегают. Процессы же теплопровод­ности, наоборот, оказывают решающее влияние на формирование температурных полей при нестационарном тепловом состоянии от­дельных тел и систем.

Процессы нестационарной теплопроводности можно разделить на две группы: а) нестационарные процессы, связанные с наруше­нием теплового равновесия, когда с течением времени система стремится к некоторому новому равновесному состоянию; б) неста­ционарные процессы, связанные с периодическим изменением тепло­вого состояния тела (периодические изменения температуры окру­жающей среды или мощности тепловых источников и т. п.).

В большинстве задач нестационарной теплопроводности требу­ется найти температуры в определенных точках тела в заданный мо­мент времени t от начала процесса. Возможна и обратная задача: найти длительность процесса, в результате которого температура в данной точке тела примет определенное, наперед заданное значе­ние. В некоторых задачах бывает необходимо найти теп­ловой поток в определенной точке в заданный момент времени или полное количество теплоты, отданной (или полученной) телом в те­чение заданного промежутка времени.

Все перечисленные задачи сводятся к нахождению температуры рассматриваемого тела как функции времени и координат t = f (t, x, у, z).

Эту зависимость можно найти, если проинтегрировать дифференциальное уравнение теплопроводности при заданных краевых условиях.

Для некоторых конкретных задач теплопроводности дифферен­циальное уравнение может быть упрощено: в случае передачи теп­лоты в одном направлении задача становится одномерной; при распростра­нении теплоты в двух направлениях задача является двухмерной. Для тел ци­линдрической формы удобно перейти к цилиндрическим координа­там, а для тел шаровой формы – к сферическим.

Дифференциальное уравнение и краевые условия полностью фор­мулируют задачу. Дальнейшее аналитическое ее решение сводится к использованию методов математической физики. Основные из них: метод разделения переменных, методы интегральных преобразований (например, Лапласа), метод мгновенных точечных источников. Кроме аналитических применяют и прибли­женные методы.

В качестве примера рассмотрим охлаждение неограниченной пластины.

Охлаждение неограниченной пластины

Будем рассматривать задачу теплопроводности при постоянных значениях теплофизических характеристик тела (l, с,r) с граничны­ми условиями третьего рода, так как они наиболее часто встреча­ются на практике. Задача формулируется следующим образом. Плоская неограни­ченная пластина толщиной d, имеющая во всех точках одинаковую начальную температуру t_нч, в момент времени t = 0 помещается в среду, температура которой t_ж < t_нч. Температура среды во время охлаждения поддерживается постоянной. Охлаждение пластины происходит через обе ее поверхности с одинаковой интенсивностью путем теплоотдачи, т.е., тепловой поток на поверхности подчиняется закону Ньютона-Рихмана q = a(t_c – t_ж). Коэффи­циент теплоотдачи a известен и не меняется в течение всего процес­са. Известен также материал, из которого выполнена пластина.

Требуется найти температурное поле пластины в произволь­ный момент времени t > 0. Математически задачу можно сформули­ровать следующим образом. Дифференциальное уравнение теплопроводности для одномерной задачи без внутренних источников тепло­ты

,

где х может изменяться в пределах 0 £ х £ d/2: так как охлаждение пластины происходит симметрич­но, целесообразно поместить на­чало координат в середину пласти­ны и рассматривать процесс толь­ко в одной ее половине (см. рисунок). Краевые условия:

1) начальное условие при t = 0 и 0 £ х £ d/2 t = t_нч;

2) граничные условия: а) при х = 0и t > 0 (дt/дx)₀ = 0, т. к. при симметричном охлаждении в середине пластины в любой момент времени температура будет максимальной; б) при х = l и t > 0 - l(дt/дx) _c = a(t_c – t_ж).

Последнее выражение записано на основании равенства тепловых потоков на поверхности пластины: подходящего к поверхности из внутренних областей тела путем теплопроводности и отводимого от поверхности в процессе теплоотдачи.

Решение задачи в общем виде можно представить как функцию независимых переменных х и t и параметров процесса а,l, a, l, t_ж, t_нч:

t = f (х,t, а,l, a, l, t_ж, t_нч).

Следуя методу подобия, приведем условия задачи к безразмер­ной форме; это значительно сокращает число переменных, придает полученному решению обобщенность, и упрощает анализ ре­шения.

Для этого произведем сначала замену искомой величи­ны t так называемой избыточной температурой J = t – t_ж.

Так как d J = dt,то запись дифференциального уравнения и гра­ничных условий от такой замены не изменится:

;

при t = 0 и 0 £ х £ l J = J _нч где J _нч = t_нч – t_ж; при х = 0, t > 0 (д J /дx)₀ = 0; при х = l и t > 0 (д J /дx) _c = -(a/l)J _с, где J _с = t_с – t_ж.

Приведем уравнение и граничные условия к безразмерному виду. Для этого еще раз произведем замену переменных: вместо избыточной температуры введем безразмерную избыточ­ную температуру Q = J/J _нч. Вместо координа­ты х введем безразмерную координату Х = х / l. Такая замена равно­сильна тому, что в качестве масштаба для измерения температуры используется величина J _нч, а в качестве масштаба длины – вели­чина l. Для сохранения равенств исходные уравнения в соответствую­щих местах необходимо умножить на масштабы температуры и длины. Тогда дифференциальное урав­нение будет иметь вид:

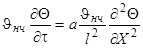, или после сокращения и преобразования .

В такой форме дифференциальное уравнение безразмерно: величина l ² /а имеет размерность времени и потому комплекс а t /l ²безразмерен. Этот комплекс обознача­ется символом Fo и называется критерием Фурье:

Fo = a t /l².

Критерий Фурье можно трактовать как безразмерное время.

Окончательно дифференциальное уравнение теплопроводности в безразмерной записи получается в следующем виде:

.

Начальное условие: при Fo = 0, Q _нч = 1;

граничные условия: при Х = 0 (д Q /дХ)₀ = 0; при X = l (д Q /дХ) _с = Bi×Q _c,

где Q _с = J _с /J _нч – безразмерная температура поверхности стенки; Bi = al /l – критерий Био.

Физический смысл критерия Био в том, что его величина характеризует соотношение интенсивностей отвода теплоты в процессе теплоотдачи и подвода теплоты из внутренних слоев тела к поверхности в результате теплопроводности.

Теперь искомая функция будет иметь вид Q = f (Fo,Bi, X).

Применяя метод разделения переменных решение дифференциального уравнения будет иметь вид

, (1)

где – коэффициенты уравнения;

m _п – корни характеристического уравнения m/Bi = ctgm.

Значения m _п и А_п приводятся в справочниках.

Результирующее выражение температурной функции, в форме произведения функции времени exp(-m²Fo) на некоторую функцию от координаты справедливо не только для пластины, но и для других тел, в которых распространение теплоты происходит в одном направлении, как, например, в бесконечно длинном цилиндре или шаре. Различаются результирующие выражения видом функции координаты: вместо cos – для пластины, для цилиндра появляется функция Бесселя, а для шара – гиперболическая. Для классических тел полу­чены аналитические решения задач нестационарной теплопроводнос­ти.

В соответствии с формой результирующих уравнений (1) порядок решения задачи нестационарной теплопроводности для тела классической формы следующий:

1. На основании исходных данных вычисляют безразмерную координату Х и критерии Bi и Fo. Здесь ха­рактерный размер тела: для пластины при симметричном охлажде­нии l = d/2,при одностороннем охлаждении l = d;для бесконечно длинного цилиндра и шара l = R,где R – радиус.

2. По величине критерия Bi в специальных таблицах нахо­дят значения m _n и А_п для нескольких значений п. В обычных инже­нерных расчетах достаточно учитывать два-четыре члена суммы в формуле (1).

3. По формуле (1) или аналогичной ей для тел другой формы вычисляют значение безразмерной температуры Q в данной точке в заданный момент времени. Из Q определяют искомую температуру t = f (t, x).

Анализ решения (1) позволяет выявить влияние величины числа Bi на нестационарную теплопроводность. Рассмотрим два предельных случая: Bi ® ¥ и Bi ® 0.

Первый предельный случай:Bi ® ¥ (практически Bi >100). Для тела конечных размеров (l – конкретная конечная величина) этот случай соответствует условию a/l ® ¥, т. е. большим значе­ниям коэффициента теплоотдачи a и сравнительно малым значениям коэффициента теплопроводности l.В этом случае сразу после начала процесса температура поверхности тела при­нимает и в дальнейшем сохраняет постоянное значение t_c = t_ж = const. Следовательно, интенсивность процесса охлаждения (нагрева) определяется внут­ренним процессом теплопроводности в теле и зависит только от фи­зических свойств и размеров тела.

При этом общее решение (1) упрощается: из числа определяющих критериев выпадает критерий Bi. Так, для точек, расположенных в средней плоскости пластины (при Х = 0), уравнение для безразмерной температуры при Fo > 0,3 приобретает вид

.

Второй предельный случай: Bi ® 0 (практически при Bi < 0,l). На практике этот случай соответствует охлаждению (или нагреву) тел малой толщины и большой теплопроводности при малом a (на­пример, тонкие металлические пластины, охлаждаемые в воздухе). В этом случае температура по всей толщине тела одна и та же в любой момент времени. Интенсивность процесса охлаждения определяется внешним процессом теплоотдачи – про­цесс выравнивания температуры внутри тела происходит гораздо интенсивнее, чем отвод теплоты от поверхности. В результате безразмерная температура всех точек пластины определяется уравнением

Q = ехр(-Bi×Fo).

Определение температуры тел ограниченных размеров

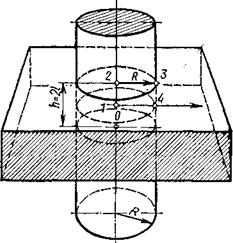Рассмотрим цилиндр конечной длины. Его можно представить как тело, образованное пересечением безграничного цилиндра радиусом R с неограниченной пластиной толщиной h = 2 l. Безразмерная температура любой точки ограниченного цилиндра представляет собой произведение безразмерных темпера­тур в соответствующих точках безграничных цилиндра и пластины, т. е.

Q = Q _ц Q _пл,

где в Q – искомая безразмерная температура; Q _ц = f_ц (Вi _ц, Fo _ц, r/R);Q _пл = f_пл (Вi _пл, Fo _пл, х/l).Соответственно Bi _u = a R/ l; Fo _ц = а t/ R ²; Bi _пл = a l/ l; Fo _пл = а t/ l ².

Величины Q _ц иQ _пл могут быть найдены по графикам с учетом расположения рассматриваемой точки в безграничном теле. Так, для точки 1 (рис.)величина Q _ц находится по графику для цент­ральных точек неограниченного цилиндра, а величина Q _пл – по гра­фику для средней плоскости пластины. Для точки 2величина Q _ц определяется по тому же графику, что и для точки 1, а Q _пл – по графику для поверхностных точек пластины. Для точки 3обе вели­чины находятся по графикам для поверхностных точек цилиндра и пластины. Для точки 4величина Q _ц определяется по графику для поверхностных точек цилиндра, а величина Q _пл – по графику для средней плоскости пластины. Перечисленные четыре точки являются характерными для огра­ниченного цилиндра. Температуры остальных точек ограниченного цилиндра по графикам не могут быть найдены, но для их определе­ния можно воспользоваться соответствующими формулами.

Аналогичные рассуждения справедливы и для параллелепипеда,но его следует рассматривать как тело, образованное пересечением трех неограниченных пластин.

 

Регулярный режим охлаждения (нагревания) тел

При значении Fo > 0,3 в выражениях типа (1) достаточно ограничиться одним первым членом ряда. В этом случае для плас­тины

. (2)

Режим охлаждения (или нагрева), определяемый формулой (2), называется регулярным. Этот результат обобщается и на более сложные задачи охлаждения (нагрева) тел любой геометрической формы при условии t_ж и a = const:

,

где m – темп охлаждения, [1/с].

В этом случае начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами.

Логарифмируя последнее уравнение, получаем:

lnJ = ln(AU) – т t, или lnJ = - т t + С (x, y, z).

Из последнего уравнения следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону. Если продифференцировать это выражение по времени получим:

.

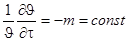В левой части уравнения стоит выражение для относительной скорости изменения температуры, и оно равняется постоянному значению т,не зависящему ни от координат, ни от времени. Следовательно, темп охлаждения характери­зует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверх­ности, геометрической формы и размеров тела.

Если экспериментально определить изменение избыточной темпера­туры Jво времени t и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регу­лярного режима найдется как

.

Выражение для зависимости темпа охлаждения т от физических свойств тела, его геометрической формы и размеров, а также условий теплооб­мена на поверхности тела можно найти из анализа теплового баланса. В результате получим:

,

где С – полная теплоемкость тела;

y = J _F /J _V – коэффициент неравномерности распределения температуры в теле;

J _F, J _V – средние по поверхности и по объему температуры тела.

Из уравнения следует, что темп охлаждения т, однородного тела при конечном значении коэффициента теплоотдачи a пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его теплоемкости (первая теорема Кондратьева).

Коэффициент y зависит от числа Bi, учитывающего условия протекания процесса на поверхности тела. Рассмотрим два предельных случая:

а) Bi ® 0 (практически Bi < 0,1). Это условие соответствует внешней задаче, когда распределение температуры в теле не зависит от его размеров и физиче­ских свойств и, следовательно, усредненные по поверхности и объему температуры будут одинаковы. Коэффициент нерав­номерности распределения температуры в теле y = 1.

б) Bi ® ¥ (практически Bi > 100). При этом условии задача становится внутренней, и процесс охлажде­ния определяется только размерами тела и его физическими свойствами. В силу большой интенсивности теплообмена температура на поверх­ности тела принимает постоянное значение, равное температуре окружаю­щей среды. Коэффициент неравномерности распределения тем­пературы y = 0.

При Bi ® ¥, или, что то же, a ® ¥, темп охлаждения т становится прямо пропорциональным коэффициенту температуропроводности тела а (вторая теорема Кондратьева):

.

Коэффициент пропорциональности К зависит от геометрической формы и размеров тела и определяется в зависимости от формы тела по выражениям:

для шара радиусом r ;

для параллелепипеда с длиной граней l ₁, l ₂, l ₃ ;

для цилиндра длиной l и радиусом r .

На основе теории регулярного режима разработаны различные экспериментальные методики определения теплофизических характеристик материалов.