Практическая работа № 1. Расчет электрической цепи постоянного тока

Практическая работа № 1

Расчет электрической цепи постоянного тока

 

Цель работы: Приобретение навыков расчёта электрической цепи постоянного тока.

Краткие теоретические сведения.

Электрической цепью называют совокуп­ность устройств, предназначенных для получения, передачи, преобразования и использования электри­ческой энергии.

Электрическая цепь состоит из отдельных уст­ройств — элементов электрической цепи.

Источниками электрической энергии являются электрические генераторы, в которых механическая энергия преобразуется в электрическую, а также пер­вичные элементы и аккумуляторы, в которых проис­ходит преобразование химической, тепловой, свето­вой и других видов энергии в электрическую.

К потребителям электрической энергии относятся электродвигатели, различные нагревательные прибо­ры, световые приборы и т. д.

Устройствами для передачи электрической энергии от ис­точников к приемникам являются линии передачи, электри­ческие сети и просто провода. Проводом называется металлическая проволока, изолированная или неизолиро­ванная (голая). Провода выполняются из меди, алюминия или стали.

Графическое изображение электрической цепи, показы­вающее последовательность соединения отдельных элемен­тов и отображающее свойства электрической цепи, назы­вается схемой электрической цепи.

При расчете цепей приходится сталкиваться с раз­личными схемами соединений потребителей. Задача расчета такой цепи состоит в том, чтобы определить токи и напряжения отдельных ее участков.

Соединение, при котором по всем участкам про­ходит один и тот же ток, называют последова­тельным. Любой замкнутый путь, проходящий по нескольким участкам, назы­вают контуром элек­трической цепи.

Участок цепи, вдоль ко­торого проходит один и тот же ток, называют ветвью, а место соединения трех и большего числа ветвей — узлом.

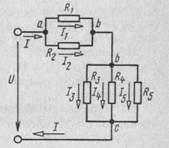
На рисунке 1 показан участок цепи, состоящей из шести ветвей и трех узлов.

Соединение, при котором все участки цепи при­соединяются к одной паре узлов, т. е. находятся под действием одного и того же напряжения, называют параллельным.

Рассмотрим различные способы соединения сопро­тивлений подробнее.

Параллельное соединение

Схема на рисунке 1 пред­ставляет собой последовательное соединение участков цепи ab и bc. В свою очередь, эти участки представ­ляют собой параллельное соединение сопротивлений. Выясним свойства такого соединения сопротивлений.

Рассмотрим соотношение токов, например, для узла а цепи. Очевидно, что ток, приходящий, к узлу, равен току, уходящему от узла:

I- I₁-I₂ = 0.

В общем виде

åI= 0 (1)

 

Это уравнение отражает первое правило Кирх­гофа: алгебраическая сумма токов ветвей для любого узла электрической цепи равна нулю.

Первое правило Кирхгофа является следствием закона сохранения заряда, согласно которому в узле заряд одного знака не может ни накапливаться, ни убывать.

 

 

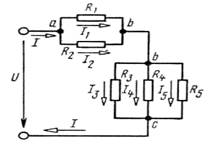
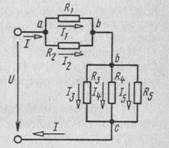
Рисунок 1-Принципиальная схема разветлённой цепи постоянного тока

 

При составлении уравнения для какого-либо узла цепи необходимо иметь в виду, что токи, направлен­ные к узлу, условились брать со знаком плюс, а токи, направленные от узла, — со знаком минус.

При параллельном соединении все ветви одним полюсом присоединяют к одному узлу, а другим — к другому. Так как потенциалы этих узлов фиксиро­ваны, то и разность их фиксирована и одинакова для всех ветвей, входящих в соединение.

Применительно к схеме рисунка 1 получим

U₁ = U₂ = U_ab, U₅= U₄= U₃= U_bс,

т. е. при параллель­ном соединении сопротивлений напряжения на ветвях одинаковы.

Применим закон Ома для всех ветвей парал­лельного разветвления на участке bс. Тогда U_bc=I₃ R₃= I₄ R₄= I₅ R₅,

откуда

I₃/I₄=R₄/R₃ и I₃/I₅=R₅/R₃

Таким образом, при параллельном соединении токи ветвей обратно пропорциональны их сопротивлениям.

Во многих случаях рассчитывают не исходные сложные, а упрощенные (эквивалентные) схемы за­мещения. Под схемой замещения понимают та­кую схему, которая обеспечивает неизменность ре­жимов работы во всех ветвях электрической цепи.

Часто приходится прибегать к замене резистивных элементов, соединенных сложным образом, одним, сопротивление которого равно общему сопротивлению исходных элементов. Найдем эквивалентное сопротив­ление при параллельном соединении ветвей, подклю­ченных к узлам b и с (рис. 1.).

Согласно первому правилу Кирхгофа, для узла b справедливо равенство

I=I₃+I₄+I₅ (2)

Вместе с тем согласно закону Ома и условию эквивалентности можно записать

I₃= U_bc/R₃, I₄=U_bc/R₄, I₅=U_bc/R₅, I= U_bc/R_эк

Подставляя эти выражения в (ф.2), получим U_bc/R_эк = U_bc/R₃+ U_bc/R₄+U_bc/R₅, откуда

L / R_эк =l/ R₃+l/ R₄+1/ R₅ (3)

Переходя от сопротивлений участков к их проводимостям, определим

g_эк = g₃+ g₄ + g₅ т (4)

В общем виде

g_эк = åg

При параллельном соединении эквивалентная, или общая, проводимость равна сумме проводимостей всех параллельных ветвей.

Определенный интерес для практики представляют два частных случая:

1) соединение состоит из двух ветвей с различными сопротивлениями;

2) соединение состоит из п ветвей с одинаковыми сопротивлениями. В первом случае, применяя формулу (ф.3), найдем

R_эк = R₁ R₂ /(R₁ + R₂) (5)

во втором

R_эк = R/ n (6)

 

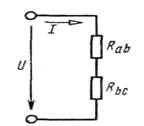
Рисунок 2-Принципиальная схема неразветлённой цепи постоянного тока

Последовательное соединение

Как указывалось, схема рис. 1. представляет собой последовательное соединение участков цепи ab и bс. Эту схему можно представить так, как показано на рис. 2., где R_ab — сопротивление, эквивалентное сопротивлению участка ab; R_bc — сопротивление, эквивалентное сопротивлению участка bс. Полученная схема представляет собой последова­тельное соединение сопротивлений.

Рассмотрим свойства последова­тельного соединения сопротивлений.

Ток в любом сечении последова­тельной цепи одинаков. Это объясня­ется тем, что ни в одной точке такой цепи не может происходить накопления зарядов.

Согласно закону сохранения энергии, напряжение на зажимах цепи равно сумме напряжений на всех ее участках:

U = U_ab + U_bc.

В общем виде

U = åU (7)

Согласно закону Ома для участка цепи можно записать

U_ab = IR_ab; U_bc = IR_bc.

Поделив приведенные равенства одно на другое, получим

U_ab/U_bc = R_ab/R_bC,

т. е. напряжения на участках цепи при последователь­ном соединении прямо пропорциональны сопротивле­ниям этих участков.

Из этого очень важного свойства вытекают усло­вия перераспределения напряжений на участках цепи при изменении сопротивлений этих участков.

В общем случае, если имеется п последова­тельно соединенных сопротивлений, согласно второму свойству,

U=U₁ + U₂ +... + U_n.

Тогда IR_эк = IR_l + IR₂ +... + IR _п

или, сократив на I,

Rэк = R₁+ R₂+... + R _n. (8) (8)

В общем виде Rэк = å R.

Смешанное соединение

Смешанное соединение представляет собой комбинацию параллельного и по­следовательного соединений сопротивлений. Опреде­лим по схеме рис. 1. токи и напряжения на всех участках цепи. Пусть напряжение на зажимах цепи U и сопротивления ее участков заданы.

Эквивалентное сопротивление цепи

Rэк = R_ab + R_bc, где R_ab = R₁R₂/(R₁+R₂); 1/R_bc= I/R₃+I/R₄ + 1/ R₅.

Общий ток источника

I=U/ Rэк,

напряжения на участках ab и bc

U_ab = IR_ab; U_bc = IR_bc.

Токи в соответствующих ветвях:

I₁ = U_ab/R₁; I₂ = U_ab/R₂; I₃=U_bc/R₃; I₄ = U_bc/R₄; I₅=U_bc/R₅.

 

Работа и мощность электрического тока.

Если электрическую цепь замкнуть, то в ней воз­никнет электрический ток. При этом энергия источника будет расходоваться. Найдем работу, которую совер­шает источник тока для перемещения заряда q по всей замкнутой цепи. Исходя из определения ЭДС получим

W_и = Eq (9)

Но так как

q = It, E=U+U_Bт,

то W_и = (U + U_BT) · It,

или

W_и =UIt + U_вт It,

где UIt = W — работа, со­вершаемая источником на внешнем участке цепи; U_вт·It = W_вт — потеря энергии внутри источника.

Используя закон Ома для участка цепи, можно за­писать

W = I²Rt = 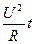. (10)

Величину, характеризуемую скоростью, с которой совершается работа, называют мощностью: P=W/t. (11)

Соответственно мощность, отдаваемая источником,

P_и = EIt/t = EI. (12)

Мощность потребителей

P = UIt/t = UI = I²R = U²/R (13)

Мощность потерь энергии внутри источника

P_вт=U_втI = I²R_вт=UI/R_вт. (14)

Единица мощности — ватт (Вт):

[ Р ]=1 Дж/1 с=1 Вт, т. е. мощность равна 1 Вт, если за 1 с совершается работа в 1 Дж.

Электрическая работа выражается в джоулях, но согласно формуле

P=W/t имеем W = Pt,

откуда 1 Дж = 1 Вт•1 с=1 Вт•с.

Баланс мощностей в цепях постоянного тока.

 

 

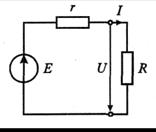
Рисунок 3- Принципиальная схема неразветлённой цепи постоянного тока с одним источником напряжения

 

Если на участке цепи с активным сопротивлением R под действи­ем приложенного к нему напряжения протекает ток I (рисунок 3), то выделяемая в нем мощность равна

Р= U·I= R·I² = g·U² (15)

эта мощность всегда положительна.

Если через источник ЭДС Е протекает ток I, то вырабатываемая им мощность равна

Р = Е·I. (16)

Она может быть положительной, когда направления Е и I совпа­дают, или отрицательной, когда их направления противоположны.

Согласно закону сохранения энергии в элементах R_k цепи по­требляется столько энергии, сколько ее отдается находящимися в ней источниками. Иначе: алгебраическая сумма мощностей, отда­ваемых всеми источниками энергии Е_i в цепи, равна сумме мощно­стей, потребляемых, в ее элементах R_k:

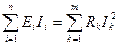(19)

Это есть уравнение баланса мощностей в цепи постоянного тока.

Запишем уравнение баланса мощностей для цепи, схе­ма которой показана на рисунке 3:

EI = rI²+RI², (20)

где EI — мощность источника ЭДС (полная мощность); RI² — мощ­ность, потребляемая нагрузкой R, rI² - мощность потерь в источ­нике ЭДС с внутренним сопротивлением r.

Мощность Р в цепях постоянного тока измеряется в ваттах (Вт).

Задание.

В цепи со смешанным соединением сопротивлений R1, R2, R3, R4, R5 и R6, вычислить токи, напряжения и мощность каждого резистора. Составить баланс мощностей.

по исходным данным (таблица 1).