Лабораторная работа №1
по дисциплине:
«Теория автоматического управления »
ОПРЕДЕЛЕНИЕ ВРЕМЕННЫХ И ЧАСТОТНЫХ ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ
Вариант 4
Выполнил: ст.гр. 121191
Илюхина И.М.
Проверил: к.т.н., доцент каф. ПУ
Матвеев В.В.
Тула 2012
Цель работы: изучение временных и частотных характеристик типовых динамических звеньев.
Теоретическая часть
Временные характеристики типовых звеньев
Динамические свойства линейных звеньев и систем автоматического управления могут быть описаны как дифференциальными уравнениями, так и графическими характеристиками. Процесс нахождения дифференциального уравнения системы через уравнения ее элементов в общем случае является довольно трудоемким. Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления в частности преобразований Лапласа. Преобразование дифференциальных уравнений по Лапласу является основой чрезвычайно удобного для исследований САУ метода передаточных функций. С помощью передаточных функций можно легко оценить динамические свойства любого элемента САУ.
Передаточной функцией W(s) звена (системы) называется отношение преобразования по Лапласу выходной координаты X(s) звена (системы) к изображению по Лапласу входной координаты Y(s) при нулевых начальных условиях:
 (1)
(1)
Под временными характеристиками динамического звена (системы) в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе звена из одного равновесного состояния в другое. Так как дифференциальное уравнение тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика представляет собой графическую форму решения дифференциального уравнения звена для принятого типового воздействия и, следовательно, полностью характеризует динамические свойства звена (системы).
|
|
Переходная функция, или переходная характеристика, h(t) описывает переходной процесс на выходе звена (системы), возникающий при подаче на его вход скачкообразного воздействия, которое мгновенно возрастает от нуля до единицы и далее остается неизменным при нулевых начальных условиях.
Единичная ступенчатая функция 1(t). Типовое входное воздействие, при котором функция y(t)=1(t) определяется соотношениями y(t) =0 при t < 0 и y(t) =1 при t³ 0, т.е.
0, т.е.
 (2)
(2)
называется единичной ступенчатой функцией 1(t) – рисунок 1а. Предполагается, что единичной ступенчатой функцией 1(t) имеет туже размерность, что и физическая величина на входе звена. Если воздействие представляет собой неединичную ступенчатую функцию y(t)=ууст.×1(t), выходная величина будет равна x(t)= ууст.h(t).
Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей системы и т.п. Умножение какой-либо функции времени x(t) на единичную ступенчатую функцию 1(t) означает, что функция времени x(t) будет существовать только при t³ 0, при t < 0 она обращается в нуль.

Рисунок 1 – Типовые входные воздействия
|
|
а – ступенчатые функции – единичная и произвольной величины;
б - единичная импульсная функция конечных параметров;
в - единичная импульсная функция нулевой ширины
Единичный импульс – дельта-функция d(t) – это математическая идеализация предельно короткого импульсного сигнала, площадь которого равна единице при длительности равной нулю, и высоте равной бесконечности. Дельта-функция представляет собой производную от единичной ступенчатой функции
d(t) =  = 1¢(t) (3)
= 1¢(t) (3)
или в операционной форме
d(s) = sL[1(t)] = s  =1. (4)
=1. (4)
Поэтому
L[w(t)] = W(s) d(s) =W(s),(5)
т.е. изображение импульсной переходной функции равно передаточной функции. Отсюда, для характеристики динамических свойств звена (системы) в равной мере могут быть использованы как передаточная, так и импульсная переходная функция. Дельта-функция тождественно равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности.
Использование ступенчатого постоянного или импульсного воздействия в виде стандартного входного сигнала имеет также и то преимущество, что действительные, любой формы, возмущающие воздействия на систему можно представить в виде последовательности таких сигналов, например так как показано на рисунке 2.

Рисунок 2 – Представление входного воздействия произвольной формы суммой входных ступенчатых воздействий
При поступлении на вход звена или разомкнутой системы с передаточной функцией W(p) входной величины y(t) = 1(t) на выходе получаем переходную характеристику x = h(t). Входная и выходная величины, преобразованные по Лапласу запишутся следующим образом
|
|
Y(p) = L[y(t)] = L[1(t)] = 1/p; (9)
X(p) = L[h(t)] = h(p). (10)
С учетом этих соотношений получим:
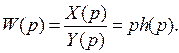 (11)
(11)
Из выражения (11) следует, что по временной характеристике системы (по переходной функции) можно получить передаточную функцию системы. В свою очередь изображение по Лапласу переходной функции определяется выражением
 (12)
(12)
Из выражения (12) с помощью обратного преобразования Лапласа можно определить переходную функцию разомкнутой системы:
 (13)
(13)
Аналогично переходная функция замкнутой системы имеет вид:
 (14)
(14)