Рассмотрим задачу об определение НДС в тонкостенных подкреплённых призматических многозамкнутых оболочках кессонного типа произвольного очертания. Решение строится в перемещениях с использованием метода В.З.Власова. Рассматриваемый метод, в отличие от балочной теории, позволяет уточнить напряженное состояние вблизи закрепления сечения оболочки на краю с координатой  (рис.8.1). При решении задачи в перемещениях за счет соответствующего подбора функций перемещения для построения решения необходимо получить уравнения равновесия. Уравнения совместности деформаций удовлетворяются автоматически за счет соответствующего выбора функций перемещений.
(рис.8.1). При решении задачи в перемещениях за счет соответствующего подбора функций перемещения для построения решения необходимо получить уравнения равновесия. Уравнения совместности деформаций удовлетворяются автоматически за счет соответствующего выбора функций перемещений.
Идея метода заключается в сведении решения уравнений равновесия в виде дифференциальных уравнениях в частных производных от двух координат к обыкновенным дифференциальным уравнениям от одной координаты.
Рассмотрим прямую кессонную часть крыла, показанного на рис.8.1 с постоянными параметрами по длине, там же показаны направления осей

Рис. 8.1. Сечение кессона крыла
координат, внешние нагрузки, направление перемещений, геометрия оболочки, направление действующих усилий в кессоне.
Введем следующие допущения для расчетной схемы оболочки:
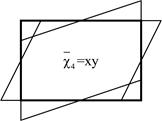
1. Контур считаем недеформируемым в своей плоскости, т.е. 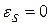 (
( координата вдоль контура оболочки).
координата вдоль контура оболочки).
2. Оболочка считается безмоментной, т.е. напряжения  ,
,  и
и 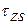 постоянны по толщине обшивки.
постоянны по толщине обшивки.
Для излагаемой задачи искомыми функциями являются перемещения в плоскости оболочки 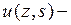 вдоль оси z,
вдоль оси z,  вдоль контура оболочки, а действующими усилиями будут
вдоль контура оболочки, а действующими усилиями будут 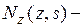 вдоль оси z,
вдоль оси z,  вдоль контура оболочки и
вдоль контура оболочки и  сдвиговые усилия.
сдвиговые усилия.
Принимаем, что все нагрузки, действующие на крыло, приведены к обобщенным силовым факторам:
- нормальной силе 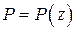 , приложенной в центре жесткости сечения;
, приложенной в центре жесткости сечения;
- изгибающим моментам относительно осей x и у -  и
и  ;
;
- крутящему моменту относительно оси z -  ;
;
- перерезывающим силам вдоль осей x и у -  и
и 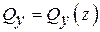 .
.
Их конкретное получение будет рассмотрено при выводе разрешающих уравнений равновесия.
В соответствии с методом В.З. Власова перемещение любой точки поверхности оболочки определяется перемещениями  и
и  , которые представляются в виде разложения в ряд
, которые представляются в виде разложения в ряд
 (j = 0, 1, 2, …, m); (8.1)
(j = 0, 1, 2, …, m); (8.1)
 (k = 1, 2, …, n), (8.2)
(k = 1, 2, …, n), (8.2)
где  и
и  - соответственно искомые продольные и поперечные перемещения, зависящие от координаты z;
- соответственно искомые продольные и поперечные перемещения, зависящие от координаты z;  и
и 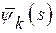 - первоначальные задаваемые функции по контуру сечения, соответствующие искомым функциям
- первоначальные задаваемые функции по контуру сечения, соответствующие искомым функциям  и
и  .
.
Тогда деформации представятся в форме
 (8.3)
(8.3)
Здесь и далее штрих при функции означает производную по соответствующей координате.
При выборе функций  и
и 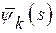 необходимо обеспечить условие непрерывности поперечных перемещений во всех точках контура. В этом случае естественно рассмотреть смещение полоски поперечного сечения. В пространстве полоска имеет шесть степеней свободы, как жесткая система, (три поступательные и три вращательные). Каждое такое смещение сечения, как жесткого целого, вызывается тремя обобщенными силами и тремя обобщенными моментами, действующими в поперечном сечении (рис.2.1) и соответствует перемещениям, которые описываются балочной теорией. Нормальная сила Р вызывает поступательное смещение полоски вдоль оси z и учитывается функцией
необходимо обеспечить условие непрерывности поперечных перемещений во всех точках контура. В этом случае естественно рассмотреть смещение полоски поперечного сечения. В пространстве полоска имеет шесть степеней свободы, как жесткая система, (три поступательные и три вращательные). Каждое такое смещение сечения, как жесткого целого, вызывается тремя обобщенными силами и тремя обобщенными моментами, действующими в поперечном сечении (рис.2.1) и соответствует перемещениям, которые описываются балочной теорией. Нормальная сила Р вызывает поступательное смещение полоски вдоль оси z и учитывается функцией  . Вращательное движение полоски при повороте относительно главных и центральных осей x и у от действия изгибающих моментов
. Вращательное движение полоски при повороте относительно главных и центральных осей x и у от действия изгибающих моментов  и
и  учитываются функциями
учитываются функциями  и
и  для оболочек произвольного сечения. Поперечные силы
для оболочек произвольного сечения. Поперечные силы  и
и  , параллельные осям x и у и действующие в сечении оболочки, вызывают смещение полоски вдоль координатных осей x и у и описываются функциями
, параллельные осям x и у и действующие в сечении оболочки, вызывают смещение полоски вдоль координатных осей x и у и описываются функциями 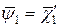 и
и  . Поворот жесткого поперечного сечения в своей плоскости относительно произвольной точки при действии крутящего момента
. Поворот жесткого поперечного сечения в своей плоскости относительно произвольной точки при действии крутящего момента  вызывает перемещение каждой точки по касательной к контуру, которое пропорционально расстоянию относительно точки поворота, и записывается в виде
вызывает перемещение каждой точки по касательной к контуру, которое пропорционально расстоянию относительно точки поворота, и записывается в виде  или
или  с учетом знака функции при обходе контура относительно направления координат. Их вид для прямоугольного сечения представлен на рис. 8.2. Таким образом, шесть искомых функций, зависящих от координаты z, соответствуют перемещениям поперечного сечения как жесткой системы:
с учетом знака функции при обходе контура относительно направления координат. Их вид для прямоугольного сечения представлен на рис. 8.2. Таким образом, шесть искомых функций, зависящих от координаты z, соответствуют перемещениям поперечного сечения как жесткой системы:  перемещение вдоль оси z;
перемещение вдоль оси z;  и
и 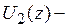 перемещения, связанные с поворотом поперечных сечений относительно осей x и у;
перемещения, связанные с поворотом поперечных сечений относительно осей x и у; 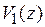 и
и  перемещения поперечных сечений вдоль осей у и x;
перемещения поперечных сечений вдоль осей у и x; 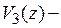 смещение сечения при его повороте. Остальные члены ряда в перемещениях (8.1) и (8.2) при
смещение сечения при его повороте. Остальные члены ряда в перемещениях (8.1) и (8.2) при 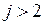 и
и  учитывают депланацию поперечного сечения и упругие перемещения вдоль контура, вызванные его деформацией. Их выбор зависит от характера нагрузки, условия закрепления оболочки, формы поперечного сечения. Например, для прямоугольного сечения при действии только изгибающих нагрузок в решении используются балочные функции
учитывают депланацию поперечного сечения и упругие перемещения вдоль контура, вызванные его деформацией. Их выбор зависит от характера нагрузки, условия закрепления оболочки, формы поперечного сечения. Например, для прямоугольного сечения при действии только изгибающих нагрузок в решении используются балочные функции  и
и  , а функцию депланации
, а функцию депланации 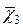 , соответствующую этой задаче, можно задать в виде параболы по горизонтальным стенкам. Если горизонтальный размер сечения гораздо больше вертикального, то явлением депланации на боковых стенках можно пренебречь. Тогда эту функцию можно представить в виде
, соответствующую этой задаче, можно задать в виде параболы по горизонтальным стенкам. Если горизонтальный размер сечения гораздо больше вертикального, то явлением депланации на боковых стенках можно пренебречь. Тогда эту функцию можно представить в виде 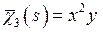 (рис.8.3). Функция депланации поперечного сечения при кручении оболочки
(рис.8.3). Функция депланации поперечного сечения при кручении оболочки  , учитывающая, что боковые стенки кессона изгибаются в противоположные стороны, если крутящий момент представить в виде пары сил показан на рис. 8.4, а саму функцию можно записать в виде
, учитывающая, что боковые стенки кессона изгибаются в противоположные стороны, если крутящий момент представить в виде пары сил показан на рис. 8.4, а саму функцию можно записать в виде 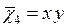 . В расчете контур считаем недеформируемым, поэтому в задаче остаются только три балочные функции
. В расчете контур считаем недеформируемым, поэтому в задаче остаются только три балочные функции  . Необходимо отметить, что представленные функции, описывающие перемещения
. Необходимо отметить, что представленные функции, описывающие перемещения



абв



г д е

Рис. 8.2. Балочные функции, определяющие перемещения и (а - в), v (г - е) по контуру
и геометрия сечения

аа


б б
Рис. 8.3. Функция депланации изгиба- Рис. 8.4. Функция депланации при стесненном
емого кессона (а) и её производная (б) кручении кессона (а) и её производная (б)
поперечного сечения, справедливы для использования в случае реального сечения силового кессона крыла.
Получим разрешающие уравнения равновесия для определения неизвестных функций  и
и  , используя вариационный принцип Лагранжа. Полная энергия системы
, используя вариационный принцип Лагранжа. Полная энергия системы 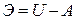 складывается из потенциальной энергии упругой деформации системы
складывается из потенциальной энергии упругой деформации системы 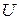 и работы внешних сил
и работы внешних сил  . Потенциальную энергию системы запишем с учетом энергии продольных элементов подкрепления оболочки в следующей форме
. Потенциальную энергию системы запишем с учетом энергии продольных элементов подкрепления оболочки в следующей форме
 , (8.4)
, (8.4)
где  ,
,  ,
,  нормальные и сдвиговые деформации в контуре оболочки;
нормальные и сдвиговые деформации в контуре оболочки; 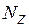 ,
, 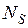 ,
,  нормальные и сдвиговые усилия в контуре оболочки;
нормальные и сдвиговые усилия в контуре оболочки;  и
и  соответственно модуль упругости и площадь поперечного сечения
соответственно модуль упругости и площадь поперечного сечения 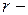 го сосредоточенного элемента, расположенного в точке сечения с координатой
го сосредоточенного элемента, расположенного в точке сечения с координатой  ;
;  длина оболочки.
длина оболочки.
Работа внешних сил в оболочке запишется в форме
 . (8.5)
. (8.5)
В рассматриваемой постановке задачи для распределенной поперечной нагрузки  контур считается жестким в своей плоскости и смещается по оси
контур считается жестким в своей плоскости и смещается по оси  на величину
на величину  , т.е.
, т.е.  , а
, а  , (8.6)
, (8.6)
где  погонная поперечная нагрузка, действующая в сечении вдоль оси у.
погонная поперечная нагрузка, действующая в сечении вдоль оси у.
Так как решение проводится в перемещениях, то в соответствии с принципом Лагранжа энергию запишем в перемещениях. Для этого усилия в записи потенциальной энергии (8.4) с помощью физического закона выразим для композиционного материала через деформации в общей форме
 ;
;
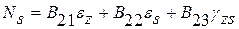 ; (8.7)
; (8.7)
 .
.
Здесь в задаче считаем, что материал конструкции ортотропный. В этом случае коэффициенты  . Подставляя в слагаемые потенциальной энергии (8.4) уравнения физического закона (8.7), а затем в выражение полной энергии, где деформации выражаем через выбранные функции перемещений (8.3), получаем полную энергию в виде
. Подставляя в слагаемые потенциальной энергии (8.4) уравнения физического закона (8.7), а затем в выражение полной энергии, где деформации выражаем через выбранные функции перемещений (8.3), получаем полную энергию в виде

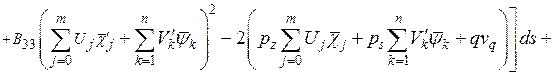
 .
.
С учетом того, что по координате 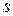 изменение функции известно, выражение полной потенциальной энергии можно представить в виде функционала от координаты
изменение функции известно, выражение полной потенциальной энергии можно представить в виде функционала от координаты 
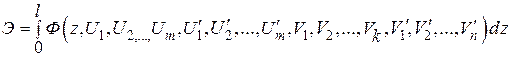 .
.
Согласно принципу Лагранжа из условия  , осуществляя варьирование функционала по неизвестным функциям, получим следующую систему дифференциальных уравнений равновесия для цилиндрической оболочки с учетом недеформируемости поперечного сечения оболочки, выполненную из ортотропного материала, и естественные статические граничные условия
, осуществляя варьирование функционала по неизвестным функциям, получим следующую систему дифференциальных уравнений равновесия для цилиндрической оболочки с учетом недеформируемости поперечного сечения оболочки, выполненную из ортотропного материала, и естественные статические граничные условия
 ;
;
 .
.  (8.8)
(8.8)
 ,
, 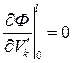 или
или  ,
,  .
.
Здесь коэффициенты, стоящие перед неизвестными функциями в уравнениях (8.8), вычисляются заранее и имеют вид:
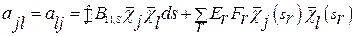 ;
;
 ,
,  ; (8.9)
; (8.9)
 ;
;  ;
;  .
.
Нижний индекс s после запятой в приведенных жесткостях обшивки оболочки 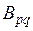 обозначает номер панели при интегрировании по контуру, в пределах которой коэффициент
обозначает номер панели при интегрировании по контуру, в пределах которой коэффициент  остается постоянным;
остается постоянным; 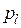 и
и  - работа внешних поверхностных сил на соответствующих перемещениях. Для недеформируемого контура эти грузовые члены приобретают конкретный смысл, связанный с типом нагружения. При действии поверхностного продольного усилия
- работа внешних поверхностных сил на соответствующих перемещениях. Для недеформируемого контура эти грузовые члены приобретают конкретный смысл, связанный с типом нагружения. При действии поверхностного продольного усилия  слагаемые при индексах
слагаемые при индексах  и
и  приобретают следующий смысл:
приобретают следующий смысл:  погонная нормальная нагрузка вдоль оси z;
погонная нормальная нагрузка вдоль оси z;  погонный изгибающий момент относительно оси y;
погонный изгибающий момент относительно оси y;  погонный изгибающий момент относительно оси x. Тогда интегрирование выражений от погонных нагрузок по координате z дает следующие силовые факторы в сечении конструкции: нормальную силу
погонный изгибающий момент относительно оси x. Тогда интегрирование выражений от погонных нагрузок по координате z дает следующие силовые факторы в сечении конструкции: нормальную силу  ; изгибающий момент в сечении вдоль оболочки относительно оси y -
; изгибающий момент в сечении вдоль оболочки относительно оси y - 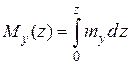 ; изгибающий момент в сечении вдоль оболочки относительно оси x -
; изгибающий момент в сечении вдоль оболочки относительно оси x -  .
.
Аналогичное интегрирование поверхностной нагрузки  , входящей в силовые слагаемые системы (8.8) при
, входящей в силовые слагаемые системы (8.8) при  , приводят к следующим погонным усилиям: к поперечной нагрузке вдоль оси
, приводят к следующим погонным усилиям: к поперечной нагрузке вдоль оси 
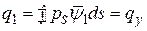 ; к поперечной нагрузке
; к поперечной нагрузке 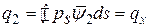 ; к погонному крутящему моменту относительно оси
; к погонному крутящему моменту относительно оси 
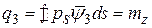 . Интегрирование выражений от погонных нагрузок по координате
. Интегрирование выражений от погонных нагрузок по координате  дает следующие силовые факторы в сечении конструкции: перерезывающую силу вдоль оси
дает следующие силовые факторы в сечении конструкции: перерезывающую силу вдоль оси 
 и перерезывающую силу
и перерезывающую силу  ; крутящий момент
; крутящий момент  . Складывая перерезывающие силы
. Складывая перерезывающие силы  из выражения (8.6) и
из выражения (8.6) и  , получим суммарную перерезывающую силу
, получим суммарную перерезывающую силу  . Если поверхностная нагрузка
. Если поверхностная нагрузка  отсутствует, то
отсутствует, то  .
.
При решении задачи в главных, центральных осях координат для рассматриваемого поперечного сечения оболочки, задаваемые функции перемещений по контурной координате s будут ортогональны между собой. Потребуем, чтобы каждая функция 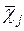 была ортогональна всем функциям
была ортогональна всем функциям  при
при  и
и  была ортогональна всем функциям
была ортогональна всем функциям  при
при  . При выполнении условия ортогонализации между функциями
. При выполнении условия ортогонализации между функциями  и функциями
и функциями  в уравнениях (8.8) коэффициенты
в уравнениях (8.8) коэффициенты  при
при  и
и  при
при  . Для выполнения этого условия введем новую функцию
. Для выполнения этого условия введем новую функцию  и
и  как линейную комбинацию функций
как линейную комбинацию функций  и
и  в виде
в виде
 ,
,  , (8.10)
, (8.10)
где  и
и  искомые коэффициенты ортогонализации. Они находятся из условия удовлетворения условия равенства нулю коэффициентов
искомые коэффициенты ортогонализации. Они находятся из условия удовлетворения условия равенства нулю коэффициентов 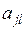 и
и  или в раскрытом виде
или в раскрытом виде

 ; (8.11)
; (8.11)

 .
.
Ортогонализация функций упрощает уравнения равновесия (8.8) и позволяет выделить из них уравнения, отвечающие решению задачи о растяжении и поперечном изгибе балки. На примере функции  , показанной на рис. 8.3, подберем новую функцию так, чтобы она стала ортогональна функциям
, показанной на рис. 8.3, подберем новую функцию так, чтобы она стала ортогональна функциям  и
и  . Для этого представим функцию
. Для этого представим функцию  в виде линейной комбинации первообразных функций
в виде линейной комбинации первообразных функций  и найдем коэффициенты
и найдем коэффициенты  и
и 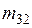 из условий ортогональности выбранных функций, т.е.
из условий ортогональности выбранных функций, т.е.  . С учетом обозначений на рис. 8.2 получим значение коэффициентов
. С учетом обозначений на рис. 8.2 получим значение коэффициентов 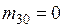 и
и  . Здесь
. Здесь 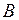 и
и 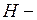 соответственно, ширина и высота кессона, а
соответственно, ширина и высота кессона, а  и
и 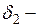 толщины вертикальной и горизонтальной стенки. Функция
толщины вертикальной и горизонтальной стенки. Функция  показана на рис. 8.3.
показана на рис. 8.3.
С учетом сформулированных упрощений, видом выбранных балочных функций и выполненных условий ортогонализации функций  и
и  можно установить величину и следующую связь между коэффициентами
можно установить величину и следующую связь между коэффициентами
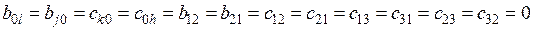 ;
;
 ;
;  .
.
Функции жесткого смещения вдоль контура  ,
,  ,
,  , как видно из рис. 8.2, будут ортогональными между собой. Для практического использования функций в решении задач учет депланации контура существенно осложняет решение, поэтому применяются только эти три функции. Зато в направлении продольной координаты можно достаточно просто получать решение с учетом депланации сечения, используя математические программы Maple, MathLab или другие программы. В этом случае система (8.8) примет вид
, как видно из рис. 8.2, будут ортогональными между собой. Для практического использования функций в решении задач учет депланации контура существенно осложняет решение, поэтому применяются только эти три функции. Зато в направлении продольной координаты можно достаточно просто получать решение с учетом депланации сечения, используя математические программы Maple, MathLab или другие программы. В этом случае система (8.8) примет вид
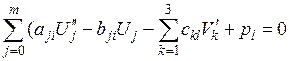 ;
;
 . (8.12)
. (8.12)
Здесь учтено, что  . При решении задачи в перемещениях методом Власова находим перемещение
. При решении задачи в перемещениях методом Власова находим перемещение  и
и  , а затем
, а затем 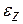 и
и  . Но поскольку при решении уравнения равновесия аппроксимирующие функции по
. Но поскольку при решении уравнения равновесия аппроксимирующие функции по  учитывают только жесткое смещение без учета деформации контура в отличие от функций для
учитывают только жесткое смещение без учета деформации контура в отличие от функций для  , то величина сдвига
, то величина сдвига  будет не точной, следовательно, и
будет не точной, следовательно, и  будет приблизительной в отличии от
будет приблизительной в отличии от  . Тогда уравнение равновесия
. Тогда уравнение равновесия 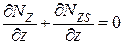 не будет точно удовлетворяться. Поэтому для определения точного значения
не будет точно удовлетворяться. Поэтому для определения точного значения  его необходимо находить из этого уравнения и дальнейшее решение для многозамкнутых контуров будет совпадать с балочной теорией при решении задач в напряжениях.
его необходимо находить из этого уравнения и дальнейшее решение для многозамкнутых контуров будет совпадать с балочной теорией при решении задач в напряжениях.
Рассмотрим примеры решения задач в перемещениях.
Пример 1. Кессон прямоугольного сечения показан на рис 8.5. Там же показаны оси координат, нагрузка и геометрия конструкции. Для рассматриваемого примера поперечного изгиба зададим по перемещению  контурные функции: балочную функцию изгиба кессона
контурные функции: балочную функцию изгиба кессона  и функцию депланации
и функцию депланации 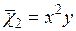 , а также функцию перемещения по контуру
, а также функцию перемещения по контуру  , определяющую перемещение
, определяющую перемещение 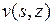 .
.

Рис. 8.5. Кессонное прямое крыло
Проведем ортогонализацию функций 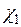 и
и  . Для этого введем новую функцию
. Для этого введем новую функцию  и найдем коэффициент ортогонализации из условия, что коэффициент
и найдем коэффициент ортогонализации из условия, что коэффициент
 .
.
Откуда находим величину коэффициента ортогонализации
 . (8.13)
. (8.13)
Для рассматриваемой задачи изгиба кессона уравнения (8.8) с учетом вида выбранных функций принимают вид:
 ;
;
 ; (8.14)
; (8.14)
 .
.
Так как  и
и  , то после интегрирования третьего уравнения можно увидеть, что полученное выражение для его первых трёх коэффициентов полностью совпадают с соответствующими коэффициентами первого уравнения. После интегрирования третье уравнение примет вид:
, то после интегрирования третьего уравнения можно увидеть, что полученное выражение для его первых трёх коэффициентов полностью совпадают с соответствующими коэффициентами первого уравнения. После интегрирования третье уравнение примет вид:
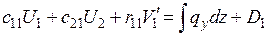 ,
,
где 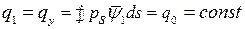 в соответствии с заданной нагрузкой (рис. 8.5). Так как после интегрирования правая часть уравнения будет равна поперечной силе
в соответствии с заданной нагрузкой (рис. 8.5). Так как после интегрирования правая часть уравнения будет равна поперечной силе  , то учитывая, что при значении
, то учитывая, что при значении 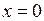 величина
величина  , константа интегрирования
, константа интегрирования 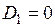 и первое граничное условие для функции
и первое граничное условие для функции  удовлетворено, а уравнение приобретает вид
удовлетворено, а уравнение приобретает вид
 . (8.15)
. (8.15)
После подстановки (8.15) в первое уравнение системы (8.14) оно преобразуется к виду
 ,
,
где  .
.
В нашей задаче  по смыслу есть изгибная жесткость кессона. Нагрузка
по смыслу есть изгибная жесткость кессона. Нагрузка  , так как отсутствует поверхностная нагрузка, и после интегрирования последнего уравнения по координате
, так как отсутствует поверхностная нагрузка, и после интегрирования последнего уравнения по координате  получим
получим
 или
или  .
.
Так как момент на краю оболочки при значении координаты  равен нулю, то константа
равен нулю, то константа  , уравнение принимает вид
, уравнение принимает вид
 .
.
Для функции 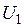 константа определена и еще одно статическое граничное условие при
константа определена и еще одно статическое граничное условие при  удовлетворено. Проинтегрировав последнее уравнение по координате
удовлетворено. Проинтегрировав последнее уравнение по координате 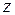 , получим решение для функции
, получим решение для функции 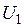 в виде
в виде
 . (8.16)
. (8.16)
Здесь константа  будет найдено из условия закрепления оболочки при значении
будет найдено из условия закрепления оболочки при значении  .
.
Исключая из второго уравнения системы (8.14) и уравнения (8.15) функцию  с помощью равенства (8.16), получим систему уравнений с оставшимися двумя другими неизвестными задачи в форме (в рассматриваемой задаче
с помощью равенства (8.16), получим систему уравнений с оставшимися двумя другими неизвестными задачи в форме (в рассматриваемой задаче  ):
):
 ;
;
 . (8.17)
. (8.17)
Исключая в системе уравнений перемещение 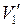 и подставляя в полученное уравнение выражение
и подставляя в полученное уравнение выражение 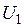 из (8.16), получим разрешающее уравнение задачи в виде
из (8.16), получим разрешающее уравнение задачи в виде
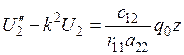 ,
,
где  , а при преобразовании системы (8.17) коэффициенты при
, а при преобразовании системы (8.17) коэффициенты при  взаимно сократились.
взаимно сократились.
Решение уравнения имеет вид
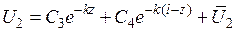 , (8.18)
, (8.18)
где частное решение  запишется
запишется  .
.
Вторую константу для функции 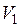 найдем интегрированием по координате
найдем интегрированием по координате  значение
значение  из второго уравнения (8.17), где функции
из второго уравнения (8.17), где функции 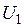 и
и  уже определены с точностью до констант. В общем виде выражение имеет вид
уже определены с точностью до констант. В общем виде выражение имеет вид
 . (8.19)
. (8.19)
Для нахождения констант  запишем граничные условия. Константа
запишем граничные условия. Константа  определяется из статического граничного условия на свободном краю кессона при
определяется из статического граничного условия на свободном краю кессона при  (условия (8.8)), которое принимает вид
(условия (8.8)), которое принимает вид

или  .
.
Для длинной оболочки, когда  , можно принять этот множитель равным нулю, тогда
, можно принять этот множитель равным нулю, тогда  .
.
Остальные константы находятся из условия закрепления края кессона при значении координаты  и принимают вид
и принимают вид
 ,
, 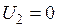 ,
,  . (8.20)
. (8.20)
Используя соотношения (8.16), (8.18) и (8.19) из условий (8.20) находим коэффициенты  ,
, 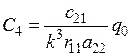 . После определения функций
. После определения функций  ,
,  , используя решение (8.19) и условие (8.20), находим коэффициент
, используя решение (8.19) и условие (8.20), находим коэффициент  .
.
В качестве примера рассмотрим прямоугольный кессон с параметрами (рис.8.6)  , нагруженный равномерной погонной нагрузкой
, нагруженный равномерной погонной нагрузкой 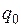 . На рис. 8.7 приведено распределение напряжений в нижней панели по длине оболочки. Сплошная линия соответствует закону плоских сечений, согласно которому напряжения распределяются равномерно по ширине панели. Пунктирные линии 1 и 2 определяют соответственно изменение напряжений вдоль края
. На рис. 8.7 приведено распределение напряжений в нижней панели по длине оболочки. Сплошная линия соответствует закону плоских сечений, согласно которому напряжения распределяются равномерно по ширине панели. Пунктирные линии 1 и 2 определяют соответственно изменение напряжений вдоль края 
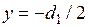 - линия 1 и
- линия 1 и 
 - линия 2. Из графика следует, что стеснение депланации сечения приводит к существенной концентрации в угловой точке сечения. Этот эффект затухает при удалении от заделанного края оболочки.
- линия 2. Из графика следует, что стеснение депланации сечения приводит к существенной концентрации в угловой точке сечения. Этот эффект затухает при удалении от заделанного края оболочки.




Рис. 8.6. Параметры сечения кессона Рис. 8.7. Распределение напряжений в
нижней панели по длине оболочки
Пример 2. Рассмотрим пример кручение кессона прямоугольного сечения, показанного на рис 8.6, нагруженного постоянным по длине погонным крутящим моментом  . Там же показаны оси координат и геометрия конструкции. Для рассматриваемого примера зададим перемещения
. Там же показаны оси координат и геометрия конструкции. Для рассматриваемого примера зададим перемещения  и
и 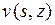 в виде
в виде
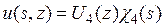 ,
,  .
.
В данном случае возьмем по одной функции в разложении ряда. Здесь задаваемая функция  , показанная на рис.8.4, характеризует депланацию сечения при кручении. Производная от этой функции представлена на рис.8.4. Функция
, показанная на рис.8.4, характеризует депланацию сечения при кручении. Производная от этой функции представлена на рис.8.4. Функция  определяет поворот сечения как жесткого диска вокруг начала координат в данной задаче и дает смещение каждой стороны пропорционально длине перпендикуляра, опущенного на каждую сторону из начала координат. Тогда из системы (8.12) разрешающие уравнения задачи примут вид
определяет поворот сечения как жесткого диска вокруг начала координат в данной задаче и дает смещение каждой стороны пропорционально длине перпендикуляра, опущенного на каждую сторону из начала координат. Тогда из системы (8.12) разрешающие уравнения задачи примут вид
 ;
;
 , (8.18)
, (8.18)
где  ;
;
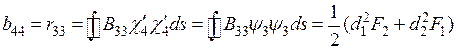 ;
;
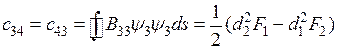 ;
;
. 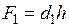 ;
; 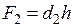 .
.
Интегрируя второе уравнение (8.18), которое принимает вид
 , (8.19)
, (8.19)
исключаем из него и первого уравнения (8.18)  получаем разрешающее уравнение для функции
получаем разрешающее уравнение для функции  . Предварительно учтем, что
. Предварительно учтем, что  (нет соответствующей нагрузи) и выражение в правой части уравнения (8.19) есть крутящий момент
(нет соответствующей нагрузи) и выражение в правой части уравнения (8.19) есть крутящий момент  . Так как момент при
. Так как момент при  тоже равен нулю, то коэффициент
тоже равен нулю, то коэффициент  . Тогда получим уравнение
. Тогда получим уравнение
 ,
,
где  .
.
Запишем решение уравнения
 .
.
Здесь частное решение равно 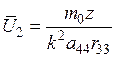 .
.
Так как перемещение  уже определено, то перемещение
уже определено, то перемещение  найдем интегрированием по координате
найдем интегрированием по координате 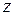 значение
значение  из второго уравнения (8.19)
из второго уравнения (8.19)
 .
.
Для нахождения констант  запишем граничные условия. Константа
запишем граничные условия. Константа  находится из условия на свободном краю кессона при
находится из условия на свободном краю кессона при  с использованием граничного условия (8.8), которое принимает вид
с использованием граничного условия (8.8), которое принимает вид
 .
.
Остальные константы находятся из условия закрепления края кессона при значении координаты  и принимают вид
и принимают вид
 ,
,  .
.
В качестве примера рассмотрим кессон, показанный на рис. 8.6, нагруженный распределённым крутящим моментом  Нм/м и имеющий следующие геометрические параметры:
Нм/м и имеющий следующие геометрические параметры:  м;
м;  м;
м;  м; суммарные толщины стенок обшивок равна
м; суммарные толщины стенок обшивок равна  м;
м;  м;
м; 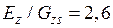 . Изменение нормальных напряжений в угловой точке сечения при удалении от закреплённого сечения показано на рис. 8.8.
. Изменение нормальных напряжений в угловой точке сечения при удалении от закреплённого сечения показано на рис. 8.8.
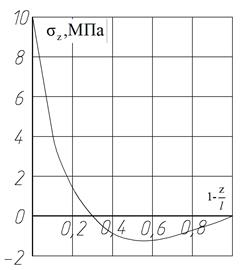
Рис. 8.8. Изменение нормальных напряжений в угловой точке сечения