Методические указания к выполнению практической работы
по курсу "Проектирование сварных конструкций"
для студентов специальности 120500
| Составитель А.А. Кречетов | |
| Утверждены на заседании кафедры Протокол №… от … | |
| Рекомендованы к печати учебно-методической комиссией специальности 120500 Протокол №… от … | |
| Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ |
Кемерово 2005
1. ЦЕЛЬ РАБОТЫ
Целью работы является закрепление теоретического материала и овладение практическими навыками проектирования сварных балок.
2. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Балкой называется конструкция, которая работает, в основном, на изгиб. Элементы балки, воспринимающие основную нагрузку и расположенные перпендикулярно плоскости действующего момента, называются полками. Элементы балки, связующие полки, называются стенками (рис. 1). Площадь поперечного сечения полок должна быть больше, чем площадь поперечного сечения стенок.

Рис.1. Консольная балка с сечением в виде сварного двутавра
Показателем экономичности сечения балки является отношение
 , ,
| (1) |
где  – момент сопротивления профиля балки;
– момент сопротивления профиля балки; 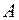 – площадь поперечного сечения профиля балки.
– площадь поперечного сечения профиля балки.
Это отношение можно увеличить путем увеличения толщины полок и уменьшения толщины стенки. Однако чрезмерное уменьшение толщины стенки может привести к потере местной устойчивости, и, как следствие, к разрушению конструкции.
Основным требованием к балкам является соблюдение необходимой жесткости, то есть прогиб балки 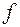 от максимальной нагрузки не должен превышать допустимых значений.
от максимальной нагрузки не должен превышать допустимых значений.
Так как прогиб балки зависит не только от действующей нагрузки, но и от ее длины, то в нормативных документах определяется предельно допустимое отношение
 , ,
| (2) |
где  – максимальный прогиб балки от максимальной нагрузки;
– максимальный прогиб балки от максимальной нагрузки; 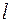 – длина балки.
– длина балки.
Норма жесткости для балок разного назначения различна. Так, например, для подкрановых балок отношение (2) должно быть в пределах 1/600…1/700, для главных балок междуэтажных перекрытий – 1/400 и т.д.
Чтобы обеспечить необходимую жесткость, высота балки должна быть не менее некоторой предельной. Для сварной консольной балки, имеющей сечение в виде двутавра, высота балки из условия обеспечения жесткости может быть приблизительно определена как

| (3) |
где  – высота балки из условия обеспечения жесткости, м;
– высота балки из условия обеспечения жесткости, м;  – действующий момент, Н·м;
– действующий момент, Н·м;  – толщина стенки балки, м;
– толщина стенки балки, м;  – максимальный прогиб балки от максимальной нагрузки, м;
– максимальный прогиб балки от максимальной нагрузки, м; 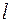 – длина балки, м;
– длина балки, м;  – модуль Юнга, Па.
– модуль Юнга, Па.
Толщина стенки балки в первом приближении может быть принята в диапазоне 5…10 мм.
Высота балки из условия минимума площади поперечного сечения профиля, обеспечивающая требуемую прочность, может быть приблизительно определена как
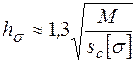 , ,
| (4) |
где 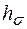 – оптимальная высота балки из условия минимума площади поперечного сечения профиля, м;
– оптимальная высота балки из условия минимума площади поперечного сечения профиля, м;  – действующий момент, Н·м;
– действующий момент, Н·м;  – толщина стенки балки, м;
– толщина стенки балки, м;  – допускаемые напряжения, Па.
– допускаемые напряжения, Па.
Высота балки, при которой с одинаковыми коэффициентами прочности выполняются условия прочности и жесткости определяется как
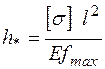 . .
| (5) |
Высота балки, рассчитанная по формулам (3)-(5), может значительно различаться. В зависимости от получившихся значений можно определить оптимальную высоту балки (табл. 1).
Таблица 1
Оптимальная высота балки
Результаты расчета  , , 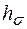 и и 
| Оптимальная высота |
 , , 
| 
|
 , , 
| 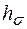
|
 , , 
| 
|
 , , 
| Выбирается высота  или или 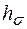 , при которой площадь поперечного сечения меньше , при которой площадь поперечного сечения меньше
|
После определения оптимальной высоты балки определяют момент инерции сечения в плоскости действия момента. Если принятая высота 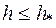 то
то
 ; ;
| (6) |
если  , то
, то
 . .
| (7) |
После определения момента инерции определяется площадь поперечного сечения полок:
 . .
| (8) |
Далее, задаваясь толщиной полки  (10…30 мм), по площади поперечного сечения полки определяют ширину полки:
(10…30 мм), по площади поперечного сечения полки определяют ширину полки:
 . .
| (9) |
После определения геометрических размеров сечения проводят проверку на прочность:
 . .
| (10) |
В выражении (10) уточненный момент инерции  необходимо рассчитать по формуле:
необходимо рассчитать по формуле:
 . .
| (11) |
В случае, если проверка (10) не выполняется, размеры сечения корректируют.
Помимо проверки на прочность необходимо выполнить проверку на общую и местную устойчивость. Потеря общей устойчивости может произойти в полке, потеря местной устойчивости – в стенке.
Проверка на общую устойчивость производят по выражению:
 , ,
| (12) |
где 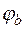 – коэффициент, определяется по вспомогательной величине
– коэффициент, определяется по вспомогательной величине
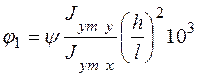 . .
| (13) |
В выражении (13)  соответствует
соответствует  , определенному по формуле (11);
, определенному по формуле (11);  вычисляется как
вычисляется как
 . .
| (14) |
Для определения коэффициента  необходимо рассчитать параметр
необходимо рассчитать параметр  :
:
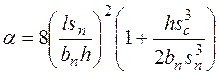 . .
| (15) |
Зная  , коэффициент
, коэффициент  определяют по табл. 2.
определяют по табл. 2.
Таблица 2
Значения коэффициента 

| 0,1 | 1,0 | 8,0 | 16,0 | 32,0 | 64,0 |

| 1,73 | 1,85 | 2,63 | 3,37 | 4,59 | 6,50 |
Значения коэффициента 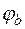 принимаются: при
принимаются: при 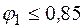
 ; при
; при 
 , но не более 1,0.
, но не более 1,0.
Местная устойчивость проверяется по формуле:
 , ,
| (16) |
где 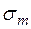 – предел текучести, МПа.
– предел текучести, МПа.
В случае если проверка на прочность выполняется, но не выполняется проверка на общую устойчивость, необходимо уменьшить толщину полки  и увеличить ее ширину
и увеличить ее ширину 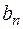 .
.
Если не выполняется условие местной устойчивости, необходимо увеличить толщину стенки  .
.
3. ВАРИАНТЫЗАДАНИЙ
В качестве задания предлагается проектирование консольной балки, имеющее сечение в виде сварного двутавра (рис. 2). Известна длина балки  и действующая сила
и действующая сила 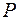 . Задан максимально допустимый прогиб
. Задан максимально допустимый прогиб  . Необходимо определить геометрические параметры сечения балки. Варианты заданий приведены в табл. 3.
. Необходимо определить геометрические параметры сечения балки. Варианты заданий приведены в табл. 3.
Таблица 3
Варианты заданий
| № |  , м , м
| 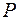 , кН , кН
| 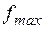 , мм , мм
| № |  , м , м
| 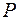 , кН , кН
|  , мм , мм
|
| 1,2 | 1,2 | ||||||
| 1,4 | 1,4 | ||||||
| 1,6 | 1,6 | ||||||
| 1,8 | 1,8 | ||||||
| 1,2 | 1,2 | ||||||
| 1,4 | 1,4 | ||||||
| 1,6 | 1,6 | ||||||
| 1,8 | 1,8 | ||||||
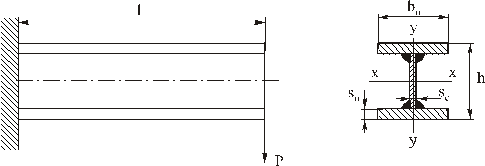
Рис. 2. Задание
Для всех вариантов:
· 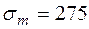 МПа;
МПа;
·  МПа.
МПа.
4. ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Исходные данные:  м;
м;  кН;
кН;  мм.
мм.
Действующий момент:
 кН·м.
кН·м.
Принимаем толщину стенки 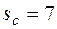 мм.
мм.
Высота из условия жесткости (3):
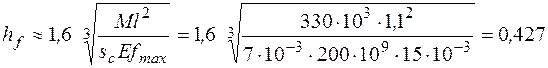 м.
м.
Высота из условия минимума площади поперечного сечения (4):
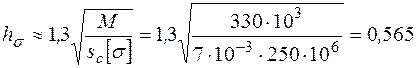 м.
м.
Высота балки, при которой с одинаковыми коэффициентами прочности выполняются условия прочности и жесткости (5):
 м.
м.
Так как в данном случае  и
и  , то оптимальной высотой балки является
, то оптимальной высотой балки является  (табл. 1).
(табл. 1).
Оптимальная высота больше, чем 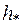 , поэтому требуемый момент инерции рассчитывается по формуле (7):
, поэтому требуемый момент инерции рассчитывается по формуле (7):
 м4.
м4.
Площадь поперечного сечения полки (8)
 м2.
м2.
Принимаем толщину полки  мм. Тогда ширина полки по формуле (9):
мм. Тогда ширина полки по формуле (9):
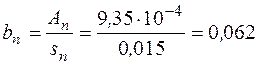 м.
м.
Для проверки спроектированной балки на прочность рассчитывается уточненный момент инерции по формуле (11):
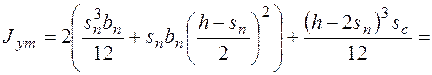

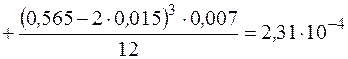 м4.
м4.
Проверка на прочность по формуле (10)
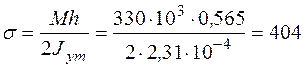 МПа.
МПа.
Напряжения, действующие в балке, значительно превосходят допускаемые. Следует скорректировать сечение таким образом, чтобы момент инерции увеличился. С этой целью геометрические размеры полки принимаются  мм,
мм,  м.
м.
Тогда

 м4.
м4.
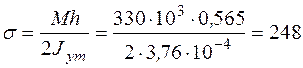 МПа.
МПа.
Далее производится проверка на общую устойчивость. Рассчитывается параметр 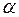 :
:
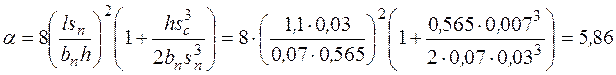
По табл. 2 принимаем  . Момент инерции в плоскости, перпендикулярной плоскости действия момента по формуле (14):
. Момент инерции в плоскости, перпендикулярной плоскости действия момента по формуле (14):

 м4.
м4.
Тогда  по формуле (13)
по формуле (13)
 .
.
Так как  , то
, то  , принимаем
, принимаем  .
.
В связи с тем, что  проверка на общую устойчивость по формуле (12) совпадает с проверкой на прочность по формуле (10). Значит, условие общей устойчивости выполняется.
проверка на общую устойчивость по формуле (12) совпадает с проверкой на прочность по формуле (10). Значит, условие общей устойчивости выполняется.
Проверка на местную устойчивость (16):
 ;
;
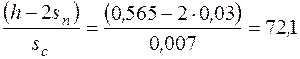 ;
;
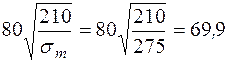 ;
;
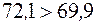 .
.
Условие местной устойчивости не соблюдается. Значит необходимо увеличить толщину стенки. Принимаем  мм. Тогда левая часть неравенства
мм. Тогда левая часть неравенства
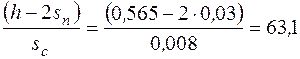 .
.
Таким образом, консольная балка длиной  м нагруженная силой
м нагруженная силой  кН при условии, что прогиб не превышает
кН при условии, что прогиб не превышает 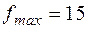 мм должна иметь сечение с размерами:
мм должна иметь сечение с размерами:
·  м;
м;
·  мм
мм
·  м;
м;
· 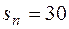 мм.
мм.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. СНиП II-23-81.Стальные конструкции
2. Николаев Г.А., Винокуров В.А. Сварные конструкции. Расчет и проектирование. – М.: Высшая школа, 1990. – 446 с.
Составитель
Кречетов Андрей Александрович