Графы
Основные понятия и алгоритмы
Понятие графа в математике является некоторой альтернативой понятию отношения (обычно бинарного отношения) на некотором конечном множестве. Наиболее близко к понятию бинарного отношения на конечном множестве стоит следующее определение. Графом (точнее – ориентированным графом) называется пара объектов G = < V, E >, состоящая из конечного множества V элементов v Î V, называемых вершинами графа, и бинарного отношения E на множестве V. Элементы отношения E называются дугами графа. Обычно граф изображают графически (отсюда – название «граф»), при этом вершины графа изображают в виде точек, а дуги изображают в виде стрелок, соединяющих первый и второй компоненты этого элемента отношения. Например, если на множестве {1, 2, 3, 4} задано отношение «меньше», то граф <{1, 2, 3, 4}, «меньше»> можно изобразить следующим образом:

Здесь вершины графа обозначены кружками, а дуги соединяют эти кружки в соответствии с определением отношения «меньше» – ведут от меньшего значения к большему. Разумеется, граф можно изобразить и по-другому. Возможно, для данного графа более естественным будет следующее изображение:
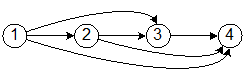
Если отношение E антирефлексивное (т.е. не содержит дуг вида (a, a)), то граф называется простым, в противном случае он называется графом с петлями (а дуги вида (a, a) называются петлями). Если отношение E симметричное, то граф называется неориентированным. В этом случае отношение всегда вместе с дугой (a, b) содержит и дугу (b, a), поэтому вместо этой пары дуг принято говорить о ребре, соединяющем вершины a и b. Соответственно, на рисунке вместо двух стрелочек изображают одну линию без стрелок, соединяющую вершины a и b.
Некоторые определения удобнее задавать в терминах рисунка, изображающего граф, чем в терминах отношений. Вот несколько определений, связанных с графами.
Вершина называется изолированной, если в нее не входит и из нее не выходит ни одна дуга. Вершина называется инцидентной дуге, если эта дуга входит в вершину или исходит из нее. Соответственно про дугу также говорят, что она инцидентна вершине (каждая дуга инцидентна ровно двум вершинам, если только она не является петлей). Вершины называются смежными, если имеется соединяющая их дуга. Степенью полузахода вершины называется количество дуг, входящих в эту вершину. Соответственно, степенью полуисхода вершины называется количество дуг, исходящих из вершины. В сумме степень полузахода и степень полуисхода вершины дает общее количество дуг, инцидентных данной вершине. Эта величина называется просто степенью вершины. Все эти определения легко модифицировать и для случая неориентированного графа (разумеется, понятия степеней полуисхода и полузахода не определены для неориентированного графа, но понятие степени вершины как число ребер, инцидентных данной вершине, определено).
Для ориентированных графов рассматривают еще вершины, из которых только исходят дуги, но не заходят в нее – такую вершину называют истоком – и вершины, в которые дуги только заходят, но не исходят – такую вершину называют стоком.
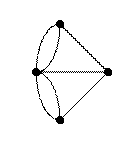
Граф называется полным, если любые две вершины в нем инцидентны друг другу. Ниже на рисунках показаны изображения полных графов с четырьмя и пятью вершинами.

Часто граф бывает интересен не сам по себе, а только в той мере, в какой он отражает реальные связи между объектами. В этом случае вершины и/или дуги бывают связаны с некоторой дополнительной информацией. Говорят, что задана нагрузочная функция (или просто нагрузка) на вершины графа, если имеется функция, сопоставляющая каждой вершине некоторый объект из нагрузочного множества f: V ® W. Аналогично другая нагрузочная функция может задавать нагрузку на дуги графа g: E ® W. Граф вместе со своими функциями нагрузки называется нагруженным графом.
Если все множество вершин графа можно разделить на два непустых множества так, что дуги всегда соединяют вершины из одного множества с вершинами из другого множества, то такой граф называется двудольным, а соответствующие множества вершин называются долями этого графа.
Если выбрать некоторое подмножество вершин A Ì V графа и некоторое подмножество дуг B Ì E, такое, что вершины, инцидентные всем дугам взяты из множества A, то пара < A, B > образует граф, называемый подграфом исходного графа. Интерес представляют две разновидности подграфов: подграф, в котором взято некоторое собственное подмножество вершин и все дуги, инцидентные этим вершинам, и подграф, в котором взяты все вершины и выбрано лишь подмножество дуг исходного графа. Первый случай называется полным подграфом исходного графа, определенным выбранным подмножеством вершин.
В графах рассматривают последовательности смежных вершин, называя их маршрутами или путями в графе. Так, в неориентированном графе маршрутом называется произвольная чередующаяся последовательность вершин и ребер v 1, e 1, v 2, e 2,…, v k, e k, v k+1, в которой соседние вершины и ребра инцидентны друг другу. Если первая вершина v 1 совпадает с последней вершиной v k+1, то маршрут называется замкнутым (или циклом). Если маршрут не содержит одинаковых вершин (кроме, быть может, первой и последней), то он называется простым маршрутом или цепью. Очевидно, что если существует некоторый маршрут, соединяющий начальную вершину v с конечной вершиной w, то существует и простой маршрут, соединяющий эти же вершины. Такой простой маршрут получится, если выкинуть из исходного маршрута циклы. Точнее говоря, если в маршруте имеются хотя бы две одинаковые вершины, то есть он имеет вид v 1,…, e i-1, v i, e i,…, e j-1, v j, e j,…, v k, причем v i = v j, то, выкинув из него последовательность v i, e i,…, e j-1, получим новый маршрут, соединяющий те же начальную и конечную вершины, но при этом из двух одинаковых вершин в нем останется только одна. Повторяя эту процедуру для всех пар совпадающих вершин, получим в конце концов простой маршрут.
Говорят, что две вершины неориентированного графа связаны, если существует маршрут, начинающийся в одной из этих вершин и кончающийся в другой. Граф называется связным, если любые его две вершины связаны. Легко проверить, что отношение связанности двух вершин рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности. Это значит, что все вершины можно разбить на классы эквивалентности связанных друг с другом вершин. Каждый такой класс эквивалентности определяет множество вершин, связанных между собой, причем ни одна вершина не может быть связана ни с какой вершиной из другого класса. Полный подграф, определенный классом связанных друг с другом вершин, называется компонентой связности исходного графа. Поскольку ни одна из вершин одной компоненты связности не может быть соединена ребром ни с какой вершиной другой компоненты связности, то все компоненты связности в совокупности образуют исходный граф и не имеют ни общих вершин, ни общих ребер. Связный граф имеет единственную компоненту связности, совпадающую со всем графом.
В теории связи графы часто используются для представления сетей связи, при этом вершины представляют узлы связи, а ребра – каналы связи. Один из самых важных вопросов в этой теории – это вопрос об устойчивости связи при выходе из строя некоторых каналов или узлов. Связь остается возможной при выходе из строя узлов или каналов в том случае, если после удаления соответствующей вершины или ребра граф остается связным. В связи с этим дадим еще несколько определений. Вершина называется точкой сочленения, если после удаления этой вершины вместе с инцидентными ей ребрами количество компонент связности графа увеличивается. Ребро называется мостом, если после удаления этого ребра количество компонент связности графа увеличивается. Очевидно, что сеть связи будет надежной, если в представляющем эту сеть связи графе не будет ни точек сочленения, ни мостов. Алгоритмы поиска мостов и точек сочленения в графе являются важными алгоритмами для исследования вопросов надежности сетей связи.
Для ориентированных графов вместо понятия маршрута используют понятие пути. Путь – это чередующаяся последовательность вершин и дуг такая v 1, e 1, v 2, e 2,…, v k, e k, v k+1, в которой каждая дуга e i выходит из вершины v i и входит в вершину v i+1. Так же, как и для маршрутов, можно определить понятие простого пути, замкнутого пути и т.п. Понятия связности и компонент связности для ориентированных графов обычно не рассматриваются.
В связи с маршрутами в графах традиционно рассматривается знаменитая задача Эйлера о «семи Кенигсбергских мостах». В этой задаче рассматривается план центральной части города Кенигсберга, в котором существенной частью являются только мосты и соединяемые ими части материка и островов. В задаче требуется построить маршрут по городу таким образом, чтобы пройти по каждому мосту ровно по одному разу. План Кенигсберга выглядит приблизительно так:

Маршрут называется Гамильтоновым, если это простой незамкнутый маршрут, содержащий все вершины графа. Гамильтоновы пути интересны в задачах, где требуется пройти по ребрам графа, побывав в каждой вершине графа по одному разу.
Маршрут называется Эйлеровым, если он содержит каждое ребро графа ровно один раз. Особый интерес представляют замкнутые Эйлеровы маршруты. В замкнутом Эйлеровом маршруте все вершины равноправны – в любой из них можно начать (и в ней же закончить) маршрут. Легко доказать, что для того, чтобы существовал замкнутый Эйлеров маршрут, необходимо, чтобы степень каждой вершины в графе была бы четной. Это следует из того, что в Эйлеровом маршруте при проходе через вершину всегда заход осуществляется по одному ребру, а выход – по другому ребру. Поскольку все ребра в Эйлеровом маршруте присутствуют ровно по одному разу и, кроме того, в каждую вершину осуществляется некоторое количество заходов и ровно такое же количество выходов, то можно сказать, что все ребра, инцидентные некоторой выбранной вершине, можно разделить на две категории: одна – это категория ребер, по которым осуществлялся заход в вершину при движении по маршруту, и вторая – это категория ребер, по которым осуществлялся выход из вершины. Этим и доказывается, что степень любой вершины четна. Точно так же можно легко показать, что в незамкнутом Эйлеровом маршруте ровно две вершины – начальная и конечная – будут иметь нечетную степень, а все остальные – четную.
Таким образом, видно, что задача Эйлера о «семи Кенигсбергских мостах» не имеет решения. Действительно, задача о мостах эквивалентна задаче о нахождении Эйлерова маршрута в графе, который получается из плана Кенигсберга, если мосты представить ребрами, а соединяемые ими части суши – вершинами графа.
На этом графе хорошо видно, что степени всех четырех вершин нечетны, следовательно Эйлерова маршрута в этом графе не существует.
Несколько труднее доказать, что если в связном графе степень любой вершины четна, то в нем существует замкнутый Эйлеров маршрут, а если имеется ровно две вершины нечетной степени, то существует Эйлеров маршрут, начинающийся в одной из них и заканчивающийся в другой.
Графы можно изображать на плоскости по-разному, однако, при этом все основные свойства графа остаются неизменными. Говорят, что два графа изоморфны, если между вершинами одного и вершинами другого графа можно установить взаимнооднозначное соответствие (изоморфизм) f такое, что если в одном графе вершины v и w соединены ребром (дугой), то и в другом графе вершины f (v) и f (w) также будут соединены ребром (дугой), и наоборот, ребро (v, w) отсутствует в одном графе, то и ребро (f (v), f (w)) будет отсутствовать в другом графе. Все свойства графов рассматривают «с точностью до изоморфизма», то есть рассматриваются только такие свойства, которые не будут изменяться при переходе от одного графа к другому, изоморфному ему графу. Граф называется планарным, если его можно изобразить на плоскости таким образом, чтобы его ребра не пересекались. Как мы видим, определение планарности графа дается так, что оно требует некоторого конкретного изображения графа, однако свойство планарности тоже инвариантно для всех изоморфных графов, поскольку требуется лишь, чтобы существовало некоторое планарное изображение графа. Так, например, оба графа, изображенные ниже на рисунке являются планарными, так как по существу это один и тот же граф (с точностью до изоморфизма), и при этом один из этих графов имеет изображение, в котором ребра не пересекаются. Изоморфизм между вершинами показан с помощью нумерации вершин – вершины с одинаковыми номерами переходят друг в друга при изоморфизме.

Поскольку каждое ребро связывает ровно две вершины, то очевидно, что в любом графе сумма степеней всех вершин равна удвоенному количеству ребер. Однако для связного планарного графа имеется и более интересное соотношение. Планарный граф при изображении его на плоскости разбивает эту плоскость на области, ограниченные ребрами графа. Оказывается, что если сложить количество таких областей (включая и внешнюю «бесконечную» область) с числом вершин графа, то всегда получится число, превышающее количество ребер на 2. Эту формулу можно доказать индукцией по числу ребер. Действительно, очевидно, что формула справедлива для графа, состоящего только из одной вершины и не имеющего ребер. Далее, если имеется связный планарный граф, содержащий k +1 ребро, то из него всегда можно удалить одно ребро так, чтобы граф оставался связным (и, разумеется, планарным). При этом возможны два случая: либо удаляемое ребро соединяет две вершины, которые связаны еще и некоторым другим маршрутом, либо ребро соединяет висячую вершину с остальной частью графа. В первом случае удаление ребра приводит к тому, что на 1 уменьшается число ребер и число областей плоскости, так что, поскольку по индукционному предположению наша формула справедлива для получившегося графа с k ребрами, то она справедлива и для исходного графа с k +1 ребром. Во втором случае число областей плоскости остается тем же самым, но на единицу уменьшается не только число ребер, но и число вершин, так что формула опять остается справедливой.
Как и для деревьев, значительный интерес представляют способы представления структуры графов и их нагрузки в памяти компьютера. Обычно в литературе рассматривают следующие способы представления графов.
Матрица смежности графа. Основой представления служит квадратная матрица размерности n, где n – количество вершин графа. В ячейках матрицы с индексами i и j указывают, каким образом связаны между собой вершины с номерами i и j. Если граф ориентированный, и необходимо только указать, имеется ли дуга, связывающая вершины i и j, то достаточно поместить в ячейку единицу или ноль (истину или ложь), которая и определяет, есть ли в графе соответствующая дуга. Для неориентированных графов ребро (i, j) одновременно является и ребром (j, i), так что элементы матрицы, расположенные симметрично относительно главной диагонали, будут совпадать. Впрочем, в этом случае избыточностью представления можно воспользоваться для размещения в матрице какой-либо дополнительной информации о нагрузке на ребра графа. Вообще, в случае нагруженного графа в матрице смежности может располагаться информация о нагрузке, при этом отсутствие дуги отмечается с помощью приписывания несуществующей дуге какого-либо «невозможного» или предельного значения нагрузки. Например, если граф представляет собой схему дорог между населенными пунктами, а нагрузка на ребра представляет собой длину дороги, то отсутствующим дорогам можно приписать бесконечно большую (или очень большую) длину.
Матрица инцидентности графа представляет собой прямоугольную матрицу размера n на m, где n – количество вершин графа, а m – количество дуг. Ячейки этой матрицы показывают, каким образом связаны вершины и дуги графа. Например, можно в ячейку с индексами i и j поместить ‑1, если дуга с номером j выходит из вершины с номером i, 1, если дуга входит в эту вершину, и 0, если дуга отсутствует. Обычно представление в виде матрицы инцидентности оказывается неэффективным, поскольку часто дуг и вершин бывает довольно много, а поскольку каждая дуга связана лишь с двумя вершинами, то почти все элементы матрицы оказываются нулевыми.
Список смежности вершин графа представляет собой набор из n списков, причем каждый i -й список содержит номера вершин, инцидентных i -й вершине. Обычно этот способ представления оказывается наиболее экономным по памяти (количество занимаемой памяти пропорционально n + m), причем в этом представлении оказывается очень удобным держать информацию о нагрузке как на дуги (в элементах списков), так и на вершины графа (в заголовках списков). Единственным существенным недостатком этого представления является то, что отсутствует мгновенный произвольный доступ к дугам. Однако в большинстве алгоритмов вполне достаточно последовательного перебора дуг, инцидентных одной вершине, который в этом представлении осуществляется достаточно быстро.
Список ребер графа представляет один последовательный список или массив, в элементах которого записывается информация о ребрах (дугах) графа, включающая номера вершин, инцидентных каждому ребру (дуге). Это представление является еще более экономным, чем предыдущее, однако, информацию о смежности вершин становится находить еще труднее, поэтому такое представление используется лишь в ограниченном числе случаев для достаточно специфичных алгоритмов.
Способы обхода (итерации) вершин и дуг графа обычно подразделяются на обходы «в глубину» (depth first) и обходы «в ширину (breadth first). При обходах в глубину порядок прохождения вершин и ребер организуется таким образом, что сразу же после прохода по некоторому ребру поиск очередного ребра производится среди тех ребер, которые исходят из вершины, в которую мы попали при последнем проходе по ребру. Если новых непройденных ребер, исходящих из этой вершины нет, то происходит возврат к предыдущей вершине и поиск нового ребра производится из нее.
При обходах «в ширину» обход производится по принципу «расходящихся кругов». Это означает, что вслед за прохождением некоторой вершины в первую очередь рассматриваются все вершины, смежные с ней, причем все эти вершины выстраиваются в обычную очередь для рассмотрения в порядке обхода. Это приводит к тому, что при таком обходе, начав с некоторой вершины, рассмотрение новых вершин продолжается для все более и более удаленных от исходной вершины вершин. Поскольку алгоритмы обходов прежде всего связаны с понятием смежности вершин, то как в обходах «в глубину», так и в обходах «в ширину» компоненты связности графа рассматриваются по отдельности.
Схематически обход «в глубину» можно представить в виде следующего алгоритма.
while (еще есть непройденные вершины) do begin
v:= (выбрать непройденную вершину);
..traverseComponent(v)
End
где рекурсивная процедура traverseComponent может быть представлена следующим алгоритмом.
procedure traverseComponent(v: integer);
Begin
(пометить v как пройденную вершину);
for w in (все вершины, смежные с v) do
if (w – непройденная вершина) then begin
(пометить ребро (v,w) как пройденное);
traverseComponent(w)
End
end;
Приведем более подробную реализацию этого алгоритма, когда граф представлен списками смежности. Перед описанием собственно алгоритма дадим описание типов для представления графа.
type PArc = ^Arc;
Arc = record e: integer; { номер вершины, в которую входит дуга }
next: PArc; { следующая дуга в списке }
end;
{ массив списков дуг, исходящих из одной и той же вершины: }
Graph = array [1..n] of PArc;
procedure traverseGraph(var g: Graph);
var mark: array [1..n] of Boolean; { помечаем пройденные вершины }
v: integer;
procedure traverseComponent(v: integer);
var w: integer;
p: PArc;
Begin
mark[v]:= true; { пометили вершину v как пройденную }
{ здесь можно выполнять действия по проходу через вершину v }
p:= g[v]; { выбрали список дуг, исходящих из v }
while p <> nil do begin
w:= p^.e;
{ здесь можно выполнять действия по проходу по дуге (v,w) }
if not mark[w] then begin
traverseComponent(w)
End
End
end;
Begin
for v:=1 to n do mark[v]:= false; { пока еще нет пройденных вершин }
for v:=1 to n do begin
if not mark[v] then { вершина v еще не пройдена }
traverseComponent(v) { обход одной компоненты связности }
End
end;
Внутри описания процедуры traverseComponent комментариями помечены те места, где надо производить действия, связанные с прохождением через вершину и.или по дуге графа. Отметим, что в случае неориентированного графа фактически по каждому ребру проход осуществляется дважды – сначала в прямом, а затем в обратном направлении. Если с проходом по ребру связано некоторое действие, которое надо проделывать только один раз, то каждое пройденное ребро придется отмечать дополнительно.
Если граф несвязный, то в самом внешнем цикле процедуры traverseGraph процедура traverseComponent будет вызвана столько раз, сколько компонент связности графа имеется. Поэтому эту процедуру обхода можно применять для определения компонент связности графа.
Тот же самый алгоритм обхода можно выразить и другим способом, без использования рекурсивных процедур. Для этого потребуется организовать еще одну структуру данных для запоминания номеров тех вершин, возврат к которым будет осуществляться при невозможности найти следующую вершину для обхода. Запоминание в этой структуре данных производится по принципу стека: доступной всегда будет только последняя добавленная компонента; она же первой будет удаляться из стека. Будем считать, что имеются функции для реализации следующих операций над стеком: добавить номер вершины в стек; взять номер вершины из стека (с удалением ее из стека); проверить, есть ли еще номера вершин в стеке, или он уже пуст. Схематически процедуру можно описать следующим образом.
while (еще есть непройденные вершины) do begin
v:= (произвольная непройденная вершина);
(поместить вершину v в стек);
(пройти компоненту связности, используя стек)
end;
при этом обход одной компоненты связности с помощью стека осуществляется с помощью следующего алгоритма:
while (стек не пуст) do begin
w:= (взять вершину из стека);
(пройти вершину w и пометить ее как пройденную);
(поместить в стек все смежные с w еще не пройденные вершины)
End
Опять, считая, что граф задан с помощью списков смежности вершин (определение типов можно взять из предыдущей процедуры обхода), уточним описание алгоритма.
procedure traverseGraph(var g: Graph);
var mark: array [1..n] of Boolean; { помечаем пройденные вершины }
s: stack; { это стек }
p: PArc; { для прохода по списку смежности }
v, u, w: integer; { промежуточные номера вершин }
Begin
s.init; { инициализация стека }
for v:=1 to n do mark[v]:= false; { пока еще нет пройденных вершин }
for v:=1 to n do { поиск непройденной вершины }
if not mark[v] then begin
s.push(v); { поместили вершину в стек }
while not s.isEmpty do begin { обход компоненты связности }
w:= s.pop; { вершина w вынимается из стека }
if not mark[w] then begin { если w не была пройдена ранее }
mark[w]:= true;
{ здесь можно выполнить действия по проходу через вершину w }
p:= g[w]; { p – начало списка смежности }
while p <> nil do begin { обход списка смежности w }
u:= p^.e;
{ здесь можно выполнить действия по проходу по дуге (w,u) }
if not mark[u] then s.push(u);
p:= p^.next
End
End
End
End
end;
Способ обхода – «в глубину» – определяется порядком помещения и извлечения вершин из стека. Заметим, что вершины графа могут попадать в стек многократно, поэтому для того, чтобы не проходить их дважды, при извлечении из стека каждая вершина вновь проверяется на предмет того, не была ли она пройдена ранее. Если изменить порядок извлечения вершин на извлечение «в порядке очереди», то есть вынимать первой ту вершину, которая была помещена в очередь ранее других, то тот же самый алгоритм (и соответствующая процедура) будут задавать порядок обхода вершин графа «в ширину».
Алгоритмы обхода графа могут применяться для самых разных целей, в том числе, для целей анализа структуры графа. Выше уже указывалось, что алгоритм обхода «в глубину» в частности определяет количество компонент связности графа. Еще одно применение данного алгоритма – это так называемая топологическая сортировка вершин ориентированного графа. Пусть ориентированный граф не имеет замкнутых цепей (замкнутая цепь в ориентированном графе называется циклом, а граф, не имеющий циклов, называется ациклическим). Тогда возможна такая нумерация вершин этого графа, что дуги всегда будут вести из вершин с меньшими номерами в вершины с большими номерами. Определение такого порядка вершин требуется во многих случаях, например, для определения критических цепей в нагруженном графе.
Топологическая сортировка вершин получится, если каждой вершине приписывать номер в следующем порядке. Вершина нумеруется в тот момент, когда уже пройдены и пронумерованы все вершины, связанные с ней цепями. Вершина получает при этом наибольший из еще не использованных номеров. Проще всего такую нумерацию продемонстрировать на процедуре рекурсивного обхода графа «в глубину». Там четко можно определить момент, когда происходит «окончательный уход» из вершины, потому что все связанные с ней вершины уже пройдены. Опишем алгоритм топологической сортировки в виде слегка модифицированной процедуры traverseGraph, причем нумерацию будем задавать с помощью дополнительного аргумента процедуры – массива номеров вершин.
type numbers = array [1..n] of integer;
procedure traverseGraph(var g: Graph; var num: numbers);
var mark: array [1..n] of Boolean; { помечаем пройденные вершины }
v, maxNum: integer;
procedure traverseComponent(v: integer);
var w: integer;
p: PArc;
Begin
mark[v]:= true; { пометили вершину v как пройденную }
p:= g[v]; { выбрали список дуг, исходящих из v }
while p <> nil do begin
w:= p^.e;
if not mark[w] then begin
traverseComponent(w)
end;
{ здесь осуществляется «окончательный» выход из вершины }
num[w]:= maxNum;
maxNum:= maxNum-1
End
end;
Begin
for v:=1 to n do mark[v]:= false; { пока еще нет пройденных вершин }
maxNum:= n; { максимальный из неиспользованных номеров вершин }
for v:=1 to n do begin
if not mark[v] then { вершина v еще не пройдена }
traverseComponent(v) { обход одной компоненты связности }
End
end;
Среди прочих алгоритмов, связанных с обходами графа, можно отметить алгоритмы определения точек сочленения и мостов в графе.
Если с каждым ребром в нагруженном неориентированном графе связано некоторое число (длина пути, пропускная способность канала и т.п.), то важными становятся алгоритмы определения не просто каких-то путей в графе, но экстремальных путей, то есть путей, имеющих максимальную или минимальную суммарную нагрузку на ребра. Мы рассмотрим два таких алгоритма: алгоритм Дейкстры, позволяющий найти путь между двумя вершинами с минимальной суммарной нагрузкой на ребра, и алгоритм Флойда, позволяющий определить минимальные пути между всеми парами вершин в графе.
Алгоритм Дейкстры (E. van Dijkstra) находит кратчайший путь (маршрут или цепь) между двумя вершинами в нагруженном графе при условии, что нагрузки на все дуги графа неотрицательны. На самом деле минимальный путь существует, если граф не содержит циклов с отрицательной суммарной нагрузкой дуг по этому циклу. Действительно, если бы такой цикл существовал, то задача нахождения пути с минимальной нагрузкой была бы бессмысленной: любой путь, проходящий хотя бы через одну вершину такого цикла, можно сделать «короче», если пройти лишний раз по циклу с отрицательной длиной.
Алгоритм немного напоминает обход графа «в ширину», начиная с первой из двух вершин, путь между которыми мы ищем. Однако, в отличие от простого обхода «в ширину» на каждом шаге мы будем рассматривать не произвольную вершину, но вершину, находящуюся на минимальном расстоянии от исходной вершины. Итак, на каждом шаге алгоритма рассматривается множество пройденных вершин и множество «вершин-кандидатов» на включение в основное множество пройденных вершин. Вершины-кандидаты – это те вершины, которые находятся на расстоянии одного шага от пройденных вершин. На каждом шаге одна из вершин-кандидатов – та, которая находится ближе других к исходной вершине, включается в основное множество пройденных вершин, при этом все соседние с ней ранее не рассмотренные вершины включаются в множество вершин-кандидатов, а если вершина уже находится в множестве вершин-кандидатов, то пересматривается ее расстояние до исходной вершины. Когда в множество пройденных вершин окажется включенной вторая из двух исходных вершин, алгоритм заканчивается.
Для каждой из вершин рассматриваемых множеств требуется хранить не только ее расстояние до исходной вершины, но и ту предыдущую вершину на пути в эту вершину, через которую достигается это минимальное расстояние. Эта информация понадобится затем для нахождения собственно самого пути.
Будем считать, что тип данных Node содержит информацию об одной вершине в виде атрибутов вершины n.number (номер вершины), n.distance (расстояние до исходной вершины) и n.previous (номер предыдущей вершины на минимальном пути в эту вершину из исходной). Тип данных NodeSet будет определять множество вершин. Будем считать, что для такого множества определены следующие операции: включение новой вершины (set.add (n)), исключение вершины (set.remove (num)), взятие вершины по номеру (set.get (num)), проверка, имеется ли в множестве определенная вершина (set.contains (num)), и есть ли вообще хоть одна вершина (set.empty). Будем также считать, что вершины множества можно перебирать в цикле с помощью абстрактной конструкции for n in set do S. Тогда алгоритм Дейкстры можно записать в виде процедуры следующим образом.
type PNode = ^Node;
Node = record number, previous:integer; distance: real end;
NodeSet = object { детали реализации скроем... } end;
PArc = ^Arc;
Arc = record e: integer; { номер вершины, в которую входит дуга }
length: real; { длина дуги }
next: PArc; { следующая дуга в списке }
end;
Graph = array [1..n] of PArc;
procedure findMinPath(var g: Graph; { исходный граф }
source, dest: integer; { номера вершин }
var path: NodeSet); { результат работы }
var aNode, nd: Node; { отдельные вершины }
candidates: NodeSet; { множество вершин-кандидатов }
current: PArc; { для просмотра дуг }
Begin
{ сначала создадим множества пройденных вершин и вершин-кандидатов }
path.init; candidates.init;
{ теперь поместим начальную вершину в множество вершин-кандидатов }
with aNode do begin
number:= source; previous:= 0; distance:= 0
end;
candidates.add(aNode);
{ основной цикл продолжается пока вершина dest не попадет в path }
while not candidates.empty and not path.has(dest) do begin
{ выберем среди вершин-кандидатов ту, которая находится
на минимальном расстоянии от исходной вершины }
aNode.distance:= maxreal;
for nd in candidates do
if nd.distance < aNode.distance then aNode:= nd;
{ переносим найденную вершину в множество пройденных вершин }
path.add(aNode); candidates.remove(aNode.number);
{ добавляем новые вершины в множество вершин-кандидатов }
current:= g[aNode.number];
while current <> nil do begin
if path.contains(current^.e) then
{ пройденные вершины не рассматриваются }
else if candidates.contains(current^.e) then begin
{ проверяем вершину-кандидат }
nd:= candidates.get(current^.e);
if nd.distance > aNode.distance + current^.length then begin
nd.distance:= aNode.distance + current^.length;
nd.previous:= aNode.number
End
Else begin
{ включаем новую вершину }
with nd do begin
number:= current^.e;
distance:= aNode.distance + current^.length;
previous:= aNode.number
end;
candidates.add(nd)
End
End
End
end;
После завершения работы процедуры в множестве path пройденных вершин будет содержаться информация обо всех вершинах, находящихся на минимальном по длине пути, ведущем из вершины source в вершину dest (если, конечно, такой путь вообще существует). Если пути из source в dest вообще нет, то в конце работы множество пройденных вершин не будет содержать информации о вершине dest вообще.
Рассмотрим теперь задачу о нахождении минимальных путей между всеми парами вершин в графе. Разумеется, искать кратчайший путь между некоторой заданной парой вершин имеет смысл только в том случае, когда такой путь вообще существует. Поэтому мы рассмотрим на самом деле две задачи – задачу определения того, между какими парами вершин существует хоть какой-нибудь путь и задачу нахождения всех кратчайших путей. В действительности эти две задачи решаются настолько похоже, что имеет смысл обе задачи решать одновременно (будем считать, что если пути между парой вершин i и j нет, то минимальное расстояние между ними бесконечно). Тем не менее, рассмотрим сначала отдельно более простую первую задачу.
Пусть граф задан своей матрицей смежности A, каждый элемент которой A [ i, j ] содержит единицу, если есть дуга, соединяющая вершину i с вершиной j и нуль, если такой дуги нет. Мы будем рассматривать также более общие матрицы A (p ), элементы которых A (p )[ i, j ] показывают, имеется ли путь из вершины i в вершину j, который либо не содержит промежуточных вершин вообще, либо все промежуточные вершины этого пути имеют номера из множества {1, 2,… p }. Таким образом, матрица A (1) – это матрица путей, не имеющих промежуточных вершин вообще или проходящих через вершину с номером 1, A (0) – матрица путей без промежуточных вершин (конечно же, это наша исходная матрица смежности A), а A (n ) – это и есть та матрица всех путей, которую мы хотим найти.
Если мы научимся по матрице A (p -1) вычислять матрицу A (p ), то задача будет решена, поскольку тогда, начав с исходной матрицы A (0) = A и последовательно вычисляя матрицы A (1), A (2),… мы в конце концов вычислим и нужную нам матрицу