Лабораторная работа № 8
Изучение свойств лазерного излучения
| Цель работы: | Изучение некоторых свойств лазерного излучения. Экспериментальное исследование распределения интенсивности света в лазерном пучке. Оценка диаметра лазерного пучка. |
Введение
Лазеры - это источники когерентного оптического излучения, принцип действия которых основан на использовании явления индуцированного излучения. Слово "лазер" представляет собой аббревиатуру английской фразы "Light Amplification by Stimulated Emission of Radiation", переводимой как усиление света в результате вынужденного излучения. Гипотеза о существовании вынужденного (индуцированного) излучения была высказана в 1917 г. А.Эйнштейном.
Открыв индуцированное излучение, А.Эйнштейн показал, что при взаимодействии электромагнитного излучения с веществом увеличение энергии поля происходит вследствие спонтанного и индуцированного излучений, а уменьшение - вследствие поглощения электромагнитного излучения. Все три явления носят случайный характер и описываются статистическими закономерностями. Вероятности индуцированного излучения и поглощения пропорциональны плотности энергии электромагнитного излучения, взаимодействующего с веществом. Индуцированное излучение возникает под воздействием электромагнитного поля при переходе частицы (атома или молекулы) с верхнего энергетического уровня на нижний. Возникшее индуцированное излучение совпадает по частоте, направлению распространения, поляризации и фазе с излучением, вызвавшим его. Именно это свойство индуцированного излучения и позволяет получить когерентное излучение с помощью лазера. При поглощении электромагнитной энергии частица (атом или молекула) переходит на энергетический уровень с большим значением энергии. Такое состояние частицы называют возбужденным. Спонтанное излучение возникает самопроизвольно при переходе частицы с верхнего уровня на нижний. Оно не зависит от внешних воздействий, а определяется только свойствами частиц.
При термодинамическом равновесии распределение частиц по энергетическим состояниям (уровням) подчиняется закону Больцмана, согласно которому вероятность пребывания атома в i- м состоянии с энергией Еi определяется выражением:
,
где C – константа; k = 1,38 ×10–23 Дж/К – постоянная Больцмана;
Т – абсолютная температура, К.
Из закона Больцмана следует, что чем больше значение энергии E i, т.е. чем выше на энергетической шкале расположен энергетический уровень, тем меньше частиц в данном ансамбле *находится в состоянии с энергией E i. Отношение же числа частиц Nm c энергией E m к числу частиц Nn c энергией E n:
.
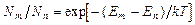Отсюда следует, что:
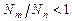, если 
.
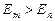Рассмотрим теперь ансамбль частиц, обладающих двумя энергетическими состояниями с энергиями Em и En, причем
Em > En, и общим числом частиц N 0. Пусть на этот ансамбль частиц воздействует излучение со спектральной плотностью потока 
и центральной частотой:
,
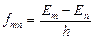где h = 6,625 10–34 Дж/с - постоянная Планка.
Если до воздействия ансамбль находился в термодинамическом равновесии, то число частиц Nm > Nn , а их отношение можно найти из закона Больцмана. При взаимодействии поля частоты fmn c ансамблем частиц будет происходить поглощение и излучение электромагнитной энергии. Энергия поля, поглощенная ансамблем частиц в единицу времени:
,
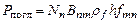а излученная:
P изл 
,
В приведенных выражениях Аmn , Bmn и Bnm - коэффициенты Эйнштейна спонтанного и индуцированного излучения, и поглощения соответственно. Указанные коэффициенты связаны следующими соотношениями:
,
где gn и gm – статистические веса** уровней n и m соответственно;
,
где с – скорость света.
Так как Amn << Bmn rf даже при малых спектральных плотностях мощности, то P изл > P погл только в том случае, когда:
,
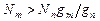или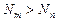 
, если gm = gn = 1.
Таким образом, для получения усиления электромагнитного поля, взаимодействующего с ансамблем частиц, необходимо, чтобы число частиц на верхнем энергетическом уровне было больше, чем на нижнем. Такое состояние ансамбля частиц называют инверсным или состоянием с инверсной населенностью. Обычно при рассмотрении процессов, происходящих в лазерах, оперируют не общим числом частиц в ансамбле, а их плотностью и обозначают ее n.
Количественное изменение интенсивности электромагнитного поля, прошедшего через ансамбль частиц, определяется законом Бугера:
,
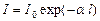где I, I 0 – интенсивность излучения на выходе из ансамбля и на входе в него соответственно;
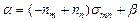– коэффициент ослабления излучения на единице длины;
smn – эффективное сечение взаимодействия излучения с частицей (характеризует вероятность поглощения или излучения фотона частицей);
b – коэффициент потерь излучения на неоднородностях ансамбля частиц (его часто называют коэффициентом нерезонансных потерь);
l – длина пути излучения в ансамбле частиц.
Ансамбль частиц будет усиливающим в том случае, если 
, т.е.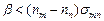 
. Это возможно только при выполнении условия nm > nn, т.е. когда в ансамбле создана инверсная населенность.
Степень усиления электромагнитного излучения определяется величиной коэффициента резонансного поглощения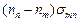 
, который, в свою очередь, определяется как свойствами частиц (smn), так и величиной плотности инверсной населенности 
. Чем больше плотность инверсной населенности, тем больше коэффициент усиления на единицу длины.
Для получения лазерного излучения ансамбль частиц должен находиться в резонаторе, который в простейшем случае представляет собой два зеркала с коэффициентами отражения r 1 и r 2. Если в ансамбле частиц, помещенном в резонатор, создать инверсную населенность, то в резонаторе возникнут колебания на частоте, соответствующей частоте перехода частиц из возбужденного состояния в основное. Незатухающие колебания будут в том случае, если плотность инверсной населенности такова, что потери на излучение и нерезонансные потери компенсированы индуцированным излучением, т.е. выполнено условие:
.
Знаку равенства соответствует установившийся режим генерации. Значение же плотности инверсной населенности, при котором выполняется указанное равенство, называется пороговым:
Dпор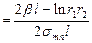 
.
Таким образом, для получения лазерного излучения необходимо иметь ансамбль частиц, в котором может быть создана инверсная населенность, резонатор и устройство, обеспечивающее получение инверсного состояния. Ансамбль частиц, в котором может быть создана инверсная населенность, называют активным веществом или активным элементом лазера. Совокупность же элементов, обеспечивающих получение инверсной населенности, называют устройством или системой накачки. Структурная схема лазера изображена на рис. 1.
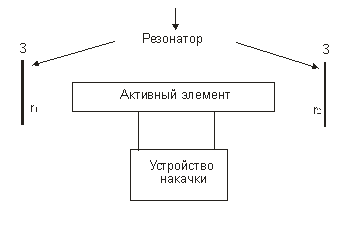
Рис. 1. Структурная схема лазера
Рассмотрим основные характеристики лазерного излучения: монохроматичность, когерентность, поляризованность, малую угловую расходимость.
В монохроматичности лазерного излучения можно убедиться, если на пути лазерного пучка поставить дифракционную решетку. Из-за монохроматичности излучения на экране возникает множество не перекрывающихся дифракционных максимумов в виде пятен или полосок одного (!) цвета.
Рис. 2
Длину волны лазерного излучения можно найти из условия максимума для дифракционной решетки:
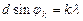, (1)
где d – постоянная дифракционной решетки (ДР), k – порядок дифракционного максимума, jk – угол, под которым наблюдается дифракционный максимум k (рис. 2). При малых углах jk можно принять, что 
sin jk » tg jk , из геометрических соображений:
,
тогда:
, (2)
где xk – координата k -того максимума, равная расстоянию от центрального (k = 0) максимума до k -того, L – расстояние от дифракционной решетки до экрана Э, на котором наблюдается дифракционная картина. Подставив (2) в (1), получим:
xk d / L = kl, откуда xk = kLl /d, или, обозначив:
A = lL / d, (3)
получим выражение для координаты xk = Ak. Координата k -того максимума увеличивается линейно с k. Коэффициент А определяется тангенсом угла наклона зависимости х = Аk.
Из (3) следует:
l = Ad /L. (4)
Формула (4) является расчетной при определении l.
Классический интерференционный опыт Юнга заключается в получении интерференционной картины от двух световых пучков, полученных в результате разделения исходного светового пучка на две части с помощью двух параллельных щелей, прорезанных в непрозрачном экране. Пространственная когерентность лазерного излучения позволяет осуществлять опыт Юнга при непосредственном освещении обеих щелей лазерным световым пучком. При этом щели в непрозрачном экране могут быть удалены друг от друга вплоть до краев сечения лазерного светового пучка на плоскости непрозрачного экрана, поскольку во всем своем сечении световой пучок пространственно когерентен.
Надо отметить, что расстояние между щелями должно быть все-таки меньше полной ширины сечения лазерного светового пучка, т.к. по мере увеличения расстояния между щелями уменьшается расстояние между интерференционными полосами на экране, и они становятся недоступными для наблюдений невооруженным глазом.
Направленность и пространственная когерентность лазерного излучения позволяют применять лазерный световой пучок в ряде измерений без предварительной его коллимации.
В поляризованности лазерного излучения можно убедиться, если между лазером и экраном поместить поляризатор. Вращая плоскость поляризатора можно наблюдать, как интенсивность светового пятна на экране зависит от угла поворота плоскости поляризатора.
Распределение интенсивности в поперечном сечении лазерного пучка подчиняется распределению Гаусса:
, (5)
где I 0 - интенсивность в центре светового пятна, х - координата, расстояние от центра светового пятна до исследуемой точки. I (x) - интенсивность на расстоянии х от центра светового пятна. Из (5) следует выражение для относительной интенсивности I / I 0:
. (6)
Характер зависимости I / I 0 от х приведен на рис. 2. Здесь параметр r - значение координаты, при которой интенсивность света I уменьшается в “ е ” раз, а относительная интенсивность:
.
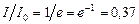Действительно, при х = r
.
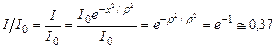Значение х = 2 ρ принимается за диаметр лазерного пучка.
Прологарифмируем выражение (6): ln(I / I 0) = – x 2 / r 2 , или:
ln(I / I 0) = (–1/ r 2) x 2. (7)
Из (7) следует, что ln(I / I 0) зависит линейно от х 2, а наклон прямой определяется коэффициентом (–1/ r 2). Таким образом, распределению Гаусса соответствует линейная зависимость ln(I / I 0) от х 2.
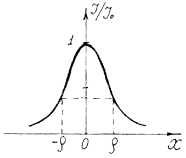
Рис. 3
С целью изучения распределения интенсивности в поперечном сечении лазерного пучка необходимо построить кривую распределения относительной интенсивности I / I 0 вдоль направления х, совпадающего с направлением горизонтального диаметра поперечного сечения лазерного пучка, т.е. найти экспериментальную зависимость I (х)/ I 0. По графику I (х)/ I 0 необходимо определить координату х, для которой I / I 0 = 0,37, приписать этой координате значение параметра r. Определить ширину пучка, приняв ее за 2 r. Затем построить график зависимости ln(I / I 0) от х 2, убедиться в его линейности, по наклону прямой определить 1/ r 2 и r, сравнить со значением r, найденным с помощью графика I (х)/ I 0.
Экспериментальная часть
Работа выполняется на установке ЛОК-1М, где в качестве источника света используется гелий-неоновый лазер. Схема установки приведена на рис. 4.
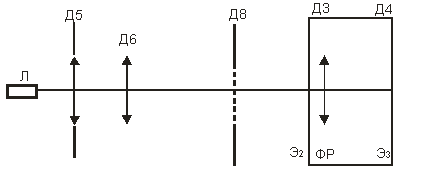Рис. 4
На оптической скамье на пути лазерного излучения устанавливаются линза Д5 и объектив Д6, на правом конце оптической скамьи – каретка фоторегистратора ФР Д3, Д4. С помощью Д5 и Д6 световой луч фокусируется на экране Э3 ФР. Экран фоторегистратора снабжен фотодатчиком, позволяющим анализировать степень освещенности данного участка экрана. Перемещая окно фотодатчика по световому пятну вдоль горизонтальной координатной прямой экрана ФР, можно проанализировать распределение интенсивности света в поперечном сечении лазерного пучка.
Порядок выполнения работы
| Упражнение 1. | Определение длины волны лазерного излучения. |
1. Соберите установку согласно схеме, приведенной на рис. 4. Перемещая Д5 и Д6, сфокусируйте световое пятно в центре экрана ФР. Между Д6 и ФР установите Д8, поместите в него экран с дифракционной решеткой № 32 (d = 0,6 мм).
2. Вращая винты Д8 и перемещая его по оптической скамье, добейтесь появления на экране Э3 четкой дифракционной картины в виде системы красных пятен, расположенных вдоль одной линии, (по 7-8 максимумов по обе стороны от центрального максимума). Разместите систему пятен вдоль горизонтальной оси экрана Э3 . Запишите значение расстояния L (рис. 2).
3. Зарисуйте дифракционную картину, приложив к экрану лист бумаги. Обозначьте центральный максимум k 0 = 0, следующие максимумы, симметрично расположенные слева и справа от центрального максимума, соответственно:
–1, +1; –2, +2; –3, +3 и т. п. Измерьте расстояния x–k,, +k между максимумами одного порядка, симметричными относительно нулевого максимума. Найдите xk:
xk = (x–k,+k)/2 b,
где β – увеличение лупы.
Данные занесите в таблицу 1.
L = м, d = м Таблица 1
| K | x –k, +k | xk |
| 1. 2. ... |
4. Постройте график зависимости xk от k. По тангенсу угла наклона графика найдите угловой коэффициент А графика линейной зависимости xk (k). и по формуле (4) рассчитайте длину волны l.
| Упражнение 2. | Качественное изучение пространственной когерентности лазерного излучения. |
Рис. 5
| Возьмите кусочек жесткой бумаги и вырежьте в нем ножницами или бритвочкой две расходящиеся щели, расположенные под некоторым углом (примерно, как показано на рис. 5, в натуральную величину). Этот самодельный экран медленно вставляйте в Д8. Наблюдайте, как изменяется дифракционная картина на экране ФР по мере увеличения расстояния между щелями и следите за тем, чтобы световое пятно на бумажном экране перекрывало обе щели. Сделайте выводы о пространственной когерентности лазерного излучения. |
| Упражнение 3. | Качественное изучение поляризованности лазерного излучения. |
С помощью Д5 и Д6 сфокусируйте световое пятно в центре экрана ФР. Вместо держателя Д8 поместите поляризатор (Д11). Вращая плоскость поляризатора, убедитесь в том, что интенсивность светового луча максимальна при некотором угле поворота, запишите значение этого угла a max. Продолжая вращать поляризатор, найдите положение, соответствующее минимальной интенсивности светового луча, запишите угол a min. Сделайте соответствующие выводы.
| Упражнение 4. | Изучение распределения интенсивности света в лазерном пучке. |
1. Снимите с оптической скамьи все держатели, кроме блока регистрации ФР (Д3, Д4). Отъюстируйте установку, выведите световое пятно в центр экрана фоторегистратора ФР, на пересечение вертикальной и горизонтальной осей. Включите фоторегистратор. При этом следите за тем, чтобы показания милливольтметра не превышали допустимого.
2. Установите фотодатчик на краю светового пятна, например, справа вдоль горизонтальной шкалы ФР. Запишите значение координаты фотодатчика на экране, L ` в мм, и показание милливольтметра фотодатчика U в мВ.
U 0 = мВ Таблица 2
| № | L ` | L = L `/ b | U | I / I 0 = U / U 0 | ln (I / I 0 ) | x | x 2 |
| 1. 2. 3. |
3. Смещая фотодатчик по диаметру светового пятна вдоль горизонтальной координатной прямой через 1 мм (один полный оборот барабана фоторегистратора), записывайте значения координат L ` и показания милливольтметра U. Полученные данные занесите в таблицу 2, приняв Umax за U 0. Полагая, что напряжение на фотодатчике пропорционально интенсивности света, U ~ I, и что I / I 0 = U / U 0, вычислите отношение I / I 0 . Учитывая увеличение лупы b = 20, найдите значение координаты L = L `/ b.
4. Постройте график распределения относительной интенсивности света в поперечном сечении светового пучка лазерного излучения I/I 0 от L (рис. 6).
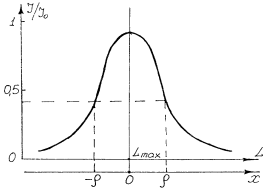
Рис. 6
5. По графику I/I 0= f (L) найдите координату L max, которой соответствует максимальная интенсивность. Примите значение этой координаты за центр светового пятна. Проведите координатную прямую х, параллельную оси L. За х = 0 примите значение L max.
6. Определите по графику координату х, для которой:
I / I 0 = 1/ e = 0,37.
В этой точке х = r = r эксп.
7. Оцените диаметр светового пятна лазерного пучка:
d = 2 r = 2 r эксп.
8. Постройте график зависимости ln(I/I 0) от х 2. Убедитесь в его линейности. Сделайте вывод: подчиняется ли распределение интенсивности в световом пучке лазерного излучения распределению Гаусса? По наклону прямой определите 1/ r 2 и вычислите r, сравните с r эксп, найденным из графика (рис. 6).
Контрольные вопросы
1. Устройство и принцип действия лазера.
2. Основные свойства лазерного излучения.
3. Как можно экспериментально убедиться в пространственной когерентности лазерного излучения?
4. Как осуществляется экспериментальная проверка монохроматичности лазерного излучения?
5. Как определить длину волны лазерного излучения?
6. Какой свет называется поляризованным? Виды поляризации. Каков характер поляризации лазерного излучения?
7. Как экспериментально убедиться в поляризованности лазерного излучения?
8. Какому распределению подчиняется распределение интенсивности света в лазерном пучке?
9. Что принимается за диаметр лазерного пучка?
10. Почему находим распределение относительной интенсивности, а не абсолютной?
* Под ансамблем частиц понимается совокупность атомов, молекул, ионов, заключенных в заданный объем и обладающих одинаковой структурой энергетических уровней.
** Числа gn и gm показывают, сколько энергетических уровней атома, молекулы или иона имеют одинаковые значения энергии En и Em соответственно.