ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ
Цель работы. Экспериментальная проверка линейной зависимости тока от напряжения I = f (U), электросопротивления от длины цилиндрического проводника R = f (l) и расчет удельного сопротивления проводника.
ПОСТАНОВКА ЗАДАЧИ
Электрический ток в металлах - это упорядоченное движение свободных электронов. При создании теории электронной проводимости металлов ее авторы (Друде, Лоренц и др.) исходили из следующих допущений.
1. Средняя кинетическая энергия поступательного движения электронов проводимости, как и у молекулы идеального газа, пропорциональна температуре металла
, (1)
где <v> - средняя скорость хаотического теплового движения, которая при комнатной температуре значительно превышает среднюю скорость упорядоченного движения <u> электронов (<v> » 105 м/с, <u> » 10-3 м/с).
2. Если внутри проводника создано электрическое поле, то каждый электрон ускоряется в течение «времени свободного пробега» t. При соударении с ионами кристаллической решетки электроны полностью отдают ионам накопленную энергию приобретенного упорядоченного движения. В результате этого металл нагревается.
Со стороны внутреннего электрического поля на электрон действует сила
F = e E, (2)
сообщая ему ускорение
. (3)
Среднее время пробега < t > на длине свободного пробега < l >
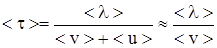. (4)
За время <t> электрон приобретает максимальную скорость дрейфа (скорость упорядоченного движения). Из (3) и (4) получим выражения для максимальной
и средней скорости дрейфа
. (5)
Рассмотрим цилиндрический участок проводника постоянного сечения dS и длиной udt. За время dt через сечение dS пройдет полный заряд
dq = en< u >dS dt. (6)
В соответствии с этим и с учетом (5) величину тока через поверхность dS определим по формуле
d I = 
= e n < u > dS.. (7)
Отношение силы тока к площади сечения, через которое он протекает, называют плотностью тока 
. Это векторная величина, совпадающая по направлению со скоростью упорядоченного движения положительного заряда в соответствии с (5) и (7), запишется
, (8)
где вектор d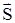 
численно равен величине элементарной площадки dS и совпадает по направлению с внешней нормалью g - удельная электропроводность вещества (g = 1/r, r - удельное электросопротивление)
Это выражение представляет закон Ома в дифференциальной форме, позволяющей найти плотность тока в любой точке проводника.
Рассмотрим однородный проводник длины l и сечения S
 |
В этом проводнике ток I = jS, а U = j1 - j2 = El (9)
Из уравнений (7) и (8) получим закон Ома в интегральной форме
, (10)
где
. (11)
Опыт показывает, что сопротивление чистых металлических проводников растет с температурой, причем в небольших интервалах температур можно считать этот рост линейным
R = R0 (1+a t0), (12)
где a » 3×10-3 1/град – температурный коэффициент сопротивления,
R0 - сопротивление проводника при 00С.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
В работе используются две электрические схемы (на установке они обозначены «Сх 1» и «Сх 2»), в которых исследуемым проводником является нихромовая проволока АВ с фиксированной длиной. Рабочий участок проволоки представлен условно отрезком ВС. В обоих схемах изменяют ток I, проходящий по проводнику АВ, регулируя напряжение питания U0. Сопротивление вольтметра обычно во много раз больше сопротивления амперметра, поэтому током через вольтметр можно пренебречь.
1. Рассмотрим схему 1. На данной схеме вольтметр измеряет напряжение U на участке проводника ВС длиной l. Фиксируя длину l и меняя ток I, с помощью потенциометра П снимают показания вольтметра. По этим данным строят вольт-амперную характеристику для участка проводника ВС=l (зависимость тока I от напряжения U при l=const, рис.3). По тангенсу угла наклона построенной прямой вычисляют среднюю величину сопротивления участка ВС по формуле
, 
.(13)
Измеряя длину участка проволоки ВС и ее диаметр, вычисляют величину среднего удельного сопротивления проводника
(14)
Оценивают по формуле
(15) значение дрейфовой скорости и сравнивают ее со средней квадратичной скоростью движения электрона, вычисленной для комнатной температуры (е=1,6×10-19 кл, n=1023 см-3).
2. Рассмотрим схему 2. В ней вольтметр измеряет напряжение на амперметре и участке проводника ВС, падения напряжения на которых равны соответственно UA и UВС , т.е. U=UА + UВС, а ток 
, где Rn - полное сопротивление проводника ВС и амперметра.
. (16)
Изменяя длину проводника ВС и фиксируя соответствующие им показания вольтметра при I=const, строят график зависимости Rn=Rn(l). Убедившись, что она имеет линейный характер, и продолжая прямую до пересечения с осью ординат, определяют внутреннее сопротивление амперметра (рис. 1). По тангенсу угла наклона прямой определяют удельное сопротивление проводника по формуле
, (17)
откуда
r = tga × S.
Конструктивно установка выполнена в одном корпусе, ручки управления находятся на передней панели корпуса.
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
 |
На рис.2 представлен общий вид установки для изучения электросопротивления нихромовой проволоки 1, натянутой между неподвижными кронштейнами 2 и 3, установленными на стойке 4. Стойка 4 закреплена на основании 5, на котором размещен блок питания (на рис. не показан). На лицевой панели 6 расположен миллиамперметр 7 и вольтметр 8. Контакт с нихромовой проволокой осуществляется токосъемным контактом 9. Величиной переходного сопротивления токосъемного контакта с проволокой в работе пренебрегаем. Длина рабочего участка нихромовой проволоки (на рис. 2 это ВС) фиксируется визирной меткой 10 на линейке 11. Номерами 12 и 13 обозначены изображенные на панели схемы «Сх 1» и «Сх 2».
Упражнение 1. Установление зависимости между током и напряжением в проводнике
1. Включить тумблер «Сеть». Должна загореться индикаторная лампочка.
2. Установить кнопку рода работ в положение «В-А» (вольтметр-амперметр). Стрелки этих приборов должны отклониться вправо.
3. Установить кнопку 14 в положение Сх 2 (рис. 1, схема 1).
4. Зафиксировать подвижный кронштейн с контактом 9 примерно посередине длины нихромовой проволоки.
5. Изменяя ток от 40 до 240 mА через 20 mA (не менее 10 раз), снимаем показания вольтметра. Данные занести в таблицу 1.
Таблица 1
| № п/п | l = | R,0 м | d, м | S, м2 | r, 0 м×м | |
| I, A | U, B | |||||
6. Построить вольт-амперную характеристику, т.е. зависимость I=f(u).
7. Найти tga.
8. Вычислить сопротивление R (формула 13) и удельное сопротивление r проволоки (формула 14).
9. Оценить дрейфовую скорость по максимальному значению тока (см. формулы (7) и (15).
Упражнение 2. Изучение зависимости сопротивления проводника от его длины.
1. Установить кнопку 14 в положение Сх 1 (рис. 1, схема 2).
2. Зафиксировать одно из значений тока в диапазоне (0,2-0,3) А.
3. Установить контакт 9 на длине проводника l - 10 см и снять показания вольтметра.
4. Увеличивая длину проводника каждый раз на Dl = 5 см, провести 6-7 измерений. Вычислить 
.
5. Занести результаты в таблицу 2.
6. Построить зависимость RВС = f (li).
Таблица 2
| № | I = | ||
| п/п | li, м | Ui, B | RBC , Ом |
8. Оценить сопротивление амперметра и сравнить его с паспортным (0,29 Ом)
9. Используя формулу (17), по тангенсу угла наклона прямой вычислить удельное сопротивление нихромовой проволоки.
10. Вычислить среднее значение удельного сопротивления <r> нихромовой проволоки по результатам заданий 1 и 2.
11. Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основные положения классической теории электропроводности металлов.
2. Условия появления и существования электрического тока.
3. Получить закон Ома в дифференциальной и интегральной форме.
4. Как определяется сопротивление и удельное сопротивление проводника в работе?
5. Как определяется сопротивление амперметра?
6. Что понимают под дрейфовой скоростью?
7. Природа линейной вольтамперной характеристики проводников.
8. Схемы включения в цепи амперметра и вольтметра.
9. Что такое электрический ток, сила тока.
10. Дайте определение и запишите формулу плотности тока.