Оптическая пространственная фильтрация.
Цель работы: изучение роли дифракционных явлений в формировании
оптических изображений.
Введение.
При изучении явлений дифракции часто сталкиваются со следующей проблемой. Известно комплексное распределение амплитуд F(η,ξ) в каком-нибудь отверстии Т плоскости А (рис. 1). Нужно найти распределение
ξ
M
с r
y
η T l
P
A o
x
B
Рис. 1
амплитуд в плоскости В, находящейся на расстоянии l от А. Формула Френеля - Кирхгофа дает возможность решить такую задачу. Пусть λ - длина волны используемого света, а r - расстояние от некоторой точки М(η, ξ) плоскости А до точки Р(х,у) плоскости В. Амплитуда f(x,y) в точке Р равна
где Т - отверстие в плоскости А. Предполагается, что линейные размеры отверстия Т алы по сравнению с расстоянием l. В том приближении
.
Тогда выражение для амплитуды в точке Р запишется в виде
. (1)
Полагая, что амплитуда F(η, ξ) тождественно равна нулю всюду, кроме отверстия Т, получим
(2)
Теперь видно, что функция f(x,y) с точностью до множителя, стоящего перед интегралом, представляет собой преобразование Фурье функции F(η,ξ)*exp[j(K/2l)(η2 + ξ2)]. Если l>>1/2K(η2 + ξ2), то функция f(x,y) будет преобразованием Фурье функции F(η,ξ), и мы переходим к дифракции Фраунгофера:
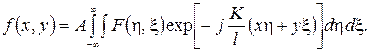(3)
Рассмотрим линзу, толщина которой в центре равна ео (рис. 2а), а на некотором расстоянии h от центра она равна е. Если n - показатель преломления материала линзы, то оптический путь луча, проходящего сквозь неё по оптической оси, будет neo. Так как линза тонкая, мы пренебрегаем отклонением луча между плоскостями А и В. Координаты точек пересечения произвольного луча с плоскостями А и В практически совпадают (рис. 2б).
e e
h h
eo eo f S'
A B
a б
Рис. 2
Луч, параллельный оптической оси и находящийся на расстоянии h от неё, проходит оптический путь ne+(eo - e). Следовательно, тонкая линза вносит изменение фазы φ = К[ne + (eo - e)].
Пусть F(η,ξ) - амплитуда падающей волны перед самой линзой (в плоскости А на рис.2а), тогда амплитуда волны F'(η,ξ) сразу после линзы (в плоскости В) будет
.
Классический расчет позволяет выразить е как функцию ео радиусов R1 и R2 поверхностей линзы, в которой толщина её равна е. Имеем
,
поэтому амплитуда запишется в виде
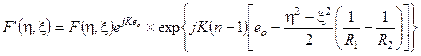, (4)
или, вводя сюда фокусное расстояние линзы f, получим
. (5)
Если на линзу падает плоская волна, как показано на рис. 2б, то F(η,ξ)=const, и воздействие линзы на волну выразится формулой
.
В рассматриваемом здесь приближении функция
описывает сферическую волну, сходящуюся при f> 0 и расходящуюся при f <0.
Рассмотрим амплитуду волны в фокальной плоскости линзы, когда объект расположен вплотную к линзе (рис. 3). F(η,ξ) - амплитуда волны, прошедшей сквозь объект. Из (5) следует, что амплитуда волны после линзы
η, ξ
x, y
A f S '
f(x, y)
Рис. 3
равна (с точностью до множителя еjKne.)
. (6)
Чтобы найти амплитуду f(x,y) в фокальной плоскости, расположенной на расстоянии f от плоскости линзы, в которой амплитуда равна F '(η,ξ), нужно применить формулу Френеля - Кирхгофа (2). Предположим, что объект меньше линзы и что конечные размеры линзы не играют роли. Используя (6), получаем
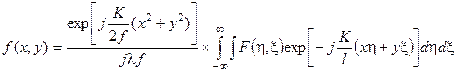. (7)
С точностью до множителя exp[j(K/2f)(x2 + y2)] зто выражение представляет собой преобразование Фурье функции F(η, ξ). Таким образом, из выражения (7) следует, что распределение комплексных амплитуд на поверхности сферы радиусом f, касающейся фокальной плоскости в точке S ', представляет собой преобразование Фурье амплитуды F(η, ξ). Следует отметить, что при решении дифракционных задач обычно ищут распределение интенсивности ff*, так что множитель перед интегралом, учитывающий фазу исчезает.
Пусть теперь объект помещен на расстоянии d от линзы и пусть Fo(ηo, ξo) - амплитуда света, прошедшего сквозь объект (рис. 4).
Fo(ηo, ξo) F(η, ξ)
d f S '
Рис. 4
Амплитуда F(η, ξ) сразу после прохождения тонкой линзы выражается по формуле Френеля-Кирхгофа (1), которую здесь мы запишем в виде
.
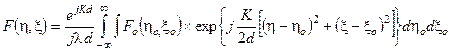Как и раньше, мы пренебрегаем конечными размерами линзы. Опуская промежуточные расчеты, амплитуда f(x,y) в фокальной плоскости линзы запишется следующим образом:
.
Из этого выражения видно, что если объект с амплитудным пропусканием Fo(ηo, ξo) расположен в передней фокальной плоскости линзы (d=f), то распределение амплитуд f(x,y) в задней фокальной плоскости представляет собой точное преобразование Фурье (фурье-образ) функции прозрачности объекта.
Рассмотрим процесс оптической фильтрации при когерентном освещении. На рис. 5 показана классическая схема оптической фильтрации. Объектом Fo(ηo, ξo) служит диапозитив или негатив, например фотопластинка с изображением пейзажа. Объект освещен параллельным пучком монохроматического света. Если он находится от линзы О2 на расстоянии f, равном её фокусному расстоянию, то преобразование Фурье объекта лежит в задней фокальной плоскости линзы О2. Это преобразование Фурье есть не что иное, как картина дифракции на объекте. Поместим в фокальной плоскости линзы О2 фильтр, который изменит распределение
Fo(ηo, ξo) Fo'(ηo', ξo')
O1 f O2 S' f O3 f
S
A Фильтр A'
Рис. 5
комплексных амплитуд в этой плоскости. Таким фильтром может быть маленький непрозрачный экран, который задерживает часть дифрагированного света в непосредственной близости от оптической оси линзы, соответствующую крупным деталям объекта (т.е. низким пространственным частотам). Экран не мешает распространению лучей, дифрагированных мелкими деталями объекта (высокие пространственные частоты) и распространяется дальше от оси. Если третья линза О3 образует в плоскости А' изображение объекта А, то крупные детали не будут воспроизведены на его изображении. Зато мелкие детали будут относительно усилены и видны лучше, что создаст впечатление увеличения четкости фотографии. Здесь приведен только один пример, но оптическая фильтрация более эффективна, если использовать разные фильтры. В некоторых областях, например при распознавании образов используются фильтры, которые регистрируют одновременно и фазу, и амплитуду. Эти фильтры представляют собой голограммы.
Рассмотрим дифракцию светового пучка на объекте, обладающем простейшей структурой. Таким объектом может служить, например, одномерная дифракционная решетка.
Если на решетку падает плоская волна, то после решетки мы будем иметь множество плоских волн, распространяющихся в направлениях, удовлетворяющих условию dsinφ=mλ, где d - период решетки, m - 0,1,2, … порядок дифракционных максимумов (рис.1).
Рис.1
Если на пути преобразованного волнового фронта поместить собирающую линзу Л, то каждая из плоских волн 0,1,2, … дает в фокальной плоскости этой линзы яркую точку S0, S1, S2, и т. д. Плоской волне, распространяющейся по какому-либо направлению, принято ставить в соответствие определенное значение пространственной частоты, которая определяется проекцией волнового вектора 
на некоторое направление, например а ось, перпендикулярную плоскости решетки. Можно сказать, таким образом, что в фокальной плоскости линзы мы наблюдаем ряд дифракционных максимумов, соответствующих множеству пространственных частот, - так называемый пространственный спектр объекта.
Собственно изображение объекта можно наблюдать за фокальной плоскостью линзы на экране или при помощи другой линзы. В предлагаемой установке объект АВ ( см. рис. 1) расположен на расстоянии порядка 2F j от линзы; следовательно, его действительное изображение A'B' будет наблюдаться также на расстоянии порядка 2F за линзой.
Теория и эксперимент показывают, что сходство объекта и его оптического изображения будет тем лучше, чем полнее используется пространственный спектр объекта. С другой стороны, если отдельные пространственные частоты исключить из процесса формирования изображения, то могут возникнуть существенные искажения изображения. Процесс изменения изображения объекта, подчеркивание его отдельных структурных особенностей путем выделения тех или иных пространственных частот носит название оптической пространственной фильтрации.
Получение возможно большей информации о свойствах объекта имеет прямое отношение к проблеме разрешающей способности оптических приборов. В частности, объектив микроскопа можно рассматривать как фильтр пространственных частот. Если оправа объектива выделяет из пространственного спектра объекта только один максимум нулевого порядка (что равносильно отсутствию дифракции на объекте), то, несмотря на то, что сквозь объектив проходит значительная световая энергия, никакой информации о структуре объекта мы не получим. Для получения минимальной информации, или как говорят, для разрешения объекта, необходимо, чтобы фильтр пропускал, по крайней мере, максимумы первых порядков, т.е. чтобы выполнялось условие
,
где d - размер объекта, n sin u - числовая апертура.
Описание экспериментальной установки.
Схема экспериментальной установки представлена на рисунке 2. Источником света может служить либо лазер 1, либо точечный источник света, помещенный в фокусе линзы и дающей параллельный пучок лучей света.
Рис. 2
Для просвечивания протяженных объектов узкий пучок лазерного излучения расширяется телескопической системой 2. Расширенный пучок света проходит через объект 3 (двумерную дифракционную решетку) и через объектив 4 с фокусным расстоянием F2 = мм. В фокальной плоскости объектива помещаются различные фильтры пространственных частот 5 - ирисовая диафрагма, или экраны с отверстиями, прорезями, сделанными в соответствии с расположением дифракционных максимумов в пространственном спектре объекта. Наблюдение изображения производится с помощью микроскопа 7. Для ослабления чрезмерной яркости картины перед микроскопом поставлен поляроид 6. Объектами, оптическое изображение которых исследуется в работе, служат двумерных дифракционные решетки и сетки.