Ряд. Сходимость рядов. Признак Даламбера
Пусть задана бесконечная последовательность чисел 
. Выражение 
называется числовым рядом. При этом числа называются членами ряда.
Числовой ряд часто записывают в виде 
.
Теорема (необходимый признак сходимости ряда). Если ряд сходится, то его 
-й член стремится к нулю при неограниченном возрастании .
Следствие. Если -й член ряда не стремится к нулю при 
, то ряд расходится.
Теорема (признак Даламбера). Если в ряде с положительными членами отношение 
-го члена ряда к -му при имеет конечный предел 
, т.е. 
, то:
- ряд сходится в случае 
,
- ряд расходится в случае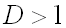 
.
В случаях, когда предел не существует или он равен единице, ответа на вопрос о сходимости или расходимости числового ряда теорема не дает. Необходимо провести дополнительное исследование.
Примеры решения задач
Пример 1. Исследовать сходимость ряда 
.
Решение.
Применим признак сходимости Даламбера. Сначала запишем формулы для -го и -го членов ряда:
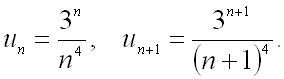
Затем найдем предел отношения -го члена ряда к -му при :
И последнее, сделаем вывод о сходимости ряда, сравнив полученное значение предела с 1. Поскольку 
, то данный ряд расходится.
Ответ: ряд расходится.
Пример 2. Исследовать сходимость ряда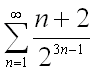 
.
Решение.
Применим признак сходимости Даламбера. Запишем формулы для -го и -го членов ряда:
Найдем предел отношения -го члена ряда к -му при :
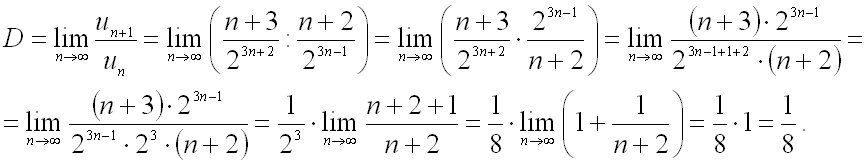
Сравним полученное значение предела с 1. Поскольку 
, то данный ряд сходится.
Ответ: ряд 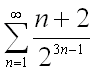сходится.
Сумма ряда.
Определение
Пусть 
— последовательность чисел. Число 
называется n -ой частичной суммой ряда 
.
Сумма (числового) ряда — это предел частичных сумм Sn, если он существует и конечен. Таким образом, если существует число 
, то в этом случае пишут 
.
Условия существования суммы ряда.
Для существования суммы числового ряда необходимо стремление его членов к нулю. Достаточные условия существования суммы ряда более сложны.
Примеры:
-
, где | q | < 1 — сумма геометрической прогрессии, в частности -
-
.
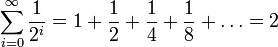
Действия с рядами.
Действия с числовыми рядами
Действия с числовыми рядами
Выделяют следующие действия с числовыми рядами (они имеют смысл, т.е. сохраняют сумму ряда, только если она существует):
- Линейная комбинация рядов
Если ряды 
и 
сходятся, то сходится и ряд 
(α, β — постоянные), при этом
- Группировка членов ряда
Сгруппируем слагаемые ряда , объединив без изменения порядка следования по нескольку (конечное число) членов ряда. Получим некоторый новый ряд . Раскрытие скобок в ряде в общем случае недопустимо, однако: если после раскрытия скобок получается сходящийся ряд, то раскрытие скобок возможно; если а каждой скобке все слагаемые имеют один и тот же знак, то раскрытие скобок не нарушает сходимости и не изменяет величину суммы.
- Перестановка членов ряда
Если ряд сходится абсолютно, то любой ряд, полученный из него перестановкой членов, также сходится абсолютно и имеет ту же сумму, что и исходный ряд. Если ряд сходится условно, то для любого наперёд заданного A (в том числе 
, 
, 
) можно так переставить члены этого ряда, что преобразованный ряд сходится к A (расходится к 
, 
, 
) либо не имеет предела (теорема Римана).