ЛАБОРАТОРНАЯ РАБОТА 6
ИЗУЧЕНИЕ ЗАКОНА МАЛЮСА
Ц е л ь р а б о т ы: Изучение явления поляризации света и проверка закона Малюса.
О б о р у д о в а н и е: Осветитель, два поляроида, фотоэлемент, гальванометр.
Теоретические сведения
Многочисленные исследования указывают на то, что свет представляет собой поперечные электромагнитные колебания, и распространяющаяся электромагнитная (световая) волна описывается тремя взаимно перпендикулярными векторами: вектором скорости 
, вектором напряженности электрического поля 
, вектором напряженности магнитного поля 
.
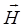Большинство источников света дают волны, в которых любое направление вектора 
в плоскости, перпендикулярной к вектору , равновероятно. Такой свет является неполяризованным или естественным. Если колебания электрического вектора фиксированы строго в одном направлении или со временем направление вектора изменяется по определенному закону, такой свет является поляризованным. Различают линейную, круговую и эллиптическую поляризации. Волна, в которой колебания совершаются в каком-то определенном направлении, является плоскополяризованной. Плоскость, проходящая через векторы и , является плоскостью поляризации.
Исследование поляризованного света производят на установке, схема которой изображена на рис.12.
Рис.12
Где S – источник света; K –конденсор; P – поляризатор; A – анализатор; Ф – фотоэлемент; Г – гальванометр; R – резистор.
Свет, проходя через поляризатор Р, становится плоскополяризованным, т.е. колебания вектора напряженности электрического, а следовательно, и магнитного поля совершаются только в определенной плоскости.
Второй поляроид – анализатор пропускает только те колебания, которые совершаются в плоскости пропускания. Если обозначить через φ угол между плоскостью пропускания анализатора и направлением крлебаний вектора напряженности электрического поля падающего на анализатор плоскополяризованного света, то интенсивность прошедшего сквозь анализатор света определится законом Малюса:
,
где Ia - интенсивность света, прошедшего через анализатор; Ip - интенсивность света на выходе поляризатора.
Из закона Малюса следует, что если плоскости пропускания поляризатора и анализатора совпадают (φ=0), то интенсивность проходящего света будет максимальной (IA= IP).
Если же анализатор будет повернут так, что его плоскость пропускания составит с плоскостью поляризатора угол 
, то интенсивность прошедшего через анализатор света будет равна нулю. В остальных случаях интенсивность прошедшего света будет принимать промежуточные значения.
 |
Для измерения светового потока используется фотоэлемент, соединенный с гальванометром. Фототок, возникающий в фотоэлементе, пропорционален падающему на катод фотоэлемента световому потоку. Фототок регистрируется гальванометром.
Измерение и обработка результатов
Проверьте схему.
Включите осветитель.
Вращая анализатор вокруг оптической оси, положение которого фиксируется по шкале на его оправе (угол 
), определите показания гальванометра. Измерения производите через каждые 10° угла поворота анализатора в диапазоне 0°- 360°. Выключите установку.
Вычислите отношение 
, где 
- показания гальванометра, соответствующее различным углам 
, 
- максимальное значение показаний гальванометра.
5. Рассчитайте величину 
, учитывая, что значению 
в законе Малюса соответствует значение 
, при котором поток, пропускаемый анализатором, максимален.
Данные измерений и вычислений занесите в таблицу 1.
Таблица 1.
| № изм. | b, град | I, мкА | I/I0, мкА | j, град | cos2j |
| … |
6. Постройте в полярных координатах график зависимости
.
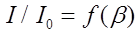Для сравнения полученных в опыте данных с теорией на том же чертеже постройте кривую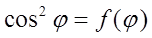 
, причем начало отсчета углов 
совместите со значением 
.
Контрольные вопросы
1. Что представляет собой плоскополяризованный?
2. В чем состоит явление двойного лучепреломления?
3. Объясните, как устроена и по какому принципу работает призма Николя.
4. Каковы условия maх и min интенсивности света в поляриметре?
Литература
1. Майсова Н.М. Практикум по курсу общей физики. М.: Высш.школа,1970, раб.64.
2. Кортнев А.В. и др. Практикум по физике. М.: Высшая школа, 1965, раб. 73.
3. Савельев И.В. Курс общей физики: В 3-х т. М.: Наука, 1982, т.3.