Определение показателя преломления
и дисперсии оптически прозрачных сред.
Цель работы: исследование зависимости показателя преломления стекла от
длины волны методом преломления света в стеклянной призме.
Введение.
При переходе из одной среды в другую свет испытывает преломление, направление распространения света меняется. Количественно это явление описывается законом Декарта-Снеллиуса (1637 г.).
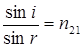 (1)
(1)
отношение синуса угла падения  к синусу угла преломления
к синусу угла преломления  есть величина постоянная для данных двух сред. Эта постоянная называется относительнымпоказателем преломления (второй среды относительно первой). Если первой средой будет вакуум, то показатель преломления называется абсолютным. Можно видеть, что относительный показатель преломления
есть величина постоянная для данных двух сред. Эта постоянная называется относительнымпоказателем преломления (второй среды относительно первой). Если первой средой будет вакуум, то показатель преломления называется абсолютным. Можно видеть, что относительный показатель преломления

равен отношению абсолютных показателей второго вещества к первому. Обычно в таблицах показателей преломления веществ даются абсолютные показатели. Для воздуха он равен практически единице. Поэтому в тех случаях, когда вещество находится в воздухе, закон (1) можно записать проще, не указывая индексы в правой части
 (2)
(2)
где  - показатель преломления вещества, указанный в таблицах.
- показатель преломления вещества, указанный в таблицах.
Показатель преломления среды - важнейшая ее характеристика, вот почему вопросу определения показателя преломления сред уделяются столь большое внимание.
В первые десятилетия после открытия закона считали это отношение постоянным. Но в 1665 г. Ньютон в своих известных опытах со стеклянной призмой (они описаны в "Оптике" Ньютона, 1704) расширил понятие показателя преломления, открыв явление, названное им дисперсией света. При пропускании пучка белого света через стеклянную призму на экране наблюдалось растянутое цветное изображение отверстия, через которое проходил белый свет (рис.1). Вверху наблюдалась красная окраска, внизу - фиолетовая. Между ними располагались прочие цвета радуги. Таким образом, дисперсия света - это явление спектрального разложения света, происходящее вследствие того, что скорость света в веществе зависит от длины волны (частоты).
|
|

Красный
Белый свет
Фиолетовый
Рис.1
Дисперсия света означает, что показатель преломления вещества не постоянен, а зависит от длины волны 
 (3)
(3)
Характер зависимости n(λ) в веществе, конкретный вид этой функции, определяется структурой вещества. Поэтому общий вид этой функции неизвестен. Принято для каждого вещества, например, для стекла определенного сорта, задавать функцию n(λ) либо в виде таблицы для известных длин волн (см. табл. 1), либо в виде графика (рис.2).
 Таблица 1.
Таблица 1.
| Длина волны лазера (нм). | Марка стекла | |
| ЛК6 (крон) | ТФ5(флинт) | |
| 1,47521 | 1,77426 | |
| 1,47371 | 1,76802 | |
| 1,47290 | 1,76470 | |
| 568,2 | 1,47121 | 1,75806 |
| 632,8 | 1,47897 | 1,74971 |
| 694,3 | 1,46732 | 1,74397 |
| 1,46371 | 1,73299 | |
| 1,46146 | 1,72765 |
Рис. 2
В сущности говоря, кривая таблично задается только в определенных точках. В промежутках же считают, что кривая идет плавно, но это предположение справедливо лишь в отсутствии поглощения. В качестве так называемого основного значения показателя преломления вещества, если дисперсия не интересует или она мала, в таблицах приводится значение nD, или указывается конкретное значение показателя преломления.
Практически как меру дисперсии, т.е. растяжения спектра, вводят величину средней дисперсии и относительной дисперсии.
|
|
 и
и  , (4)
, (4)
где nD - желтая линия натрия (589,3 нм); nC - красная линия водорода (656,3 нм); nF - зелено-голубая линия водорода (486,1 нм); nG - синяя линия водорода (434,1 нм).
Самым важным оптическим материалом является стекло. В зависимости от примесей (свинца и др. металлов) различают стекла сорта флинт (тяжёлые, с большим показателем n) n >1,60; и легкие крон, с n= 1,45 - 1,60. Однако дисперсия у крона больше, чем у флинта. Поэтому комбинация стекол с разными свойствами позволяет строить оптические системы, исправленные от различного рода аберраций.
В настоящей работе исследуется дисперсия света в стекле методом преломления света в стеклянной призме. Если на стеклянную призму с преломляющим углом А подает узкий пучок монохроматического света, то,

A
δ
i1 r1 r2 i2
Рис. 3
вследствие преломления на обеих гранях призмы, он выйдет отклонившись на угол d от первоначального направления. Из рис.3 видно, что
 , (5)
, (5)
где r1 и r2 - соответствующие i1 и i2 углы преломления; учитывая А, получаем
δ = i1 + i2 - A. (6)
Опыт показывает, что при изменении угла падения i1 в пределах от 0 до 90о угол смещения d тоже меняется, но при этом наблюдается одно единственное значение угла i1, при котором d = dmin, т.е. при некотором значении угла падения угол смещения луча, прошедшего сквозь призму, будет наименьшим из возможных. Для того, чтобы найти это значение угла, нужно исследовать выражение (5) на экстремум.


Так как  (угол i1 изменяется), то
(угол i1 изменяется), то  .
.
Поскольку углы i1 и i2 отсчитываются по разные стороны от нормали, мы можем опустить знак минус и писать далее для абсолютного значения углов. Интегрируя последнее выражение, получаем i1 = i2 = const.
|
|
В геометрической оптике хорошо известен принцип обратимости: при изменении направления всех лучей в системе на противоположные их относительное расположение не меняется. Поэтому, если смотреть на ход лучей в обратном направлении, то следует писать  i2= i1 = const.
i2= i1 = const.
Но последние два равенства возможны лишь в случае, если постоянная const = 0; или угол отклонения лучей призмой будет наименьшим из возможных, если  i1 = i2. Тогда
i1 = i2. Тогда
r1 = r2 (7)
Итак, если луч внутри призмы идет перпендикулярно биссектрисе преломляющего угла А, то смещение d прошедшего через призму монохроматического луча будет наименьшим, dmin. Из (5), (6) и (7) получим
А=2r
d min=2i - А (8)
Заменим углы i и r в законе преломления sin i/ sin r = n углами А и dmin, получим формулу для определения показателя преломления методом трехгранной призмы
 (9)
(9)
Как видно, вместо трудноизмеримых углов i и r задача свелась к нахождению углов А и d min, а это вполне выполнимо.