Лабораторная работа № 7
Изучение дифракции Фраунгофера
от одной щели
| Цель работы: | Изучение распределения интенсивно-сти в картине дифракции от узкой ще-ли при наблюдении в свете лазера. |
Введение
Дифракция Фраунгофера наблюдается в параллельных лучах, получаемых при помощи оптических систем - коллиматоров. При использовании лазера оптическая система значительно упрощается, так как излучаемые лазером когерентные световые лучи являются практически параллельными и не требуют применения оптических систем для их коллимации.

Рис. 1
Схема наблюдения дифракции Фраунгофера от одной щели представлена на рис. 1. Луч Не-Ne - лазера 1 падает нормально на щель 2, длина которой много больше ее ширины b. Согласно принципу Гюйгенса, каждая точка плоскости щели, до которой дошло световое колебание, становится источником вторичных волн, распространяющихся во все стороны под углами дифракции j 1 , j 2 ,..., т.е. свет дифрагирует при прохождении через щель. Дифрагированные пучки являются когерентными и могут интерферировать при наложении. Результат интерференции в виде периодического распределения интенсивности света наблюдается на экране 3, находящемся на расстоянии l >> b 2/l от щели 2.
Распределение интенсивности света в получаемой картине определяется суммированием элементарных волн, пришедших в данную точку экрана от всех элементов щели, с учетом их амплитуды и фазы по принципу Гюйгенса-Френеля.
При небольших углах дифракции наиболее просто рассчитать интенсивность графическим методом, предложенным Френелем. Для этого разобьем открытую часть волнового фронта в плоскости щели на узкие полоски – зоны равной ширины, параллельные краям щели. В данном случае фронт волны в плоскости щели совпадает с волновой поверхностью, т.е. фаза во всех его точках одинакова. Каждая зона (полоска) будет играть роль элементарного вторичного источника волн. Колебание DА от каждой зоны имеет одинаковую амплитуду и отстает от предыдущего колебания по фазе на одну и ту же величину d, зависящую от угла дифракции j, определяющего направление на точку наблюдения. При j0 = 0 разность фаз d равна нулю и векторная диаграмма имеет вид, показанный на рис. 2, а.

Рис. 2
Амплитуда результирующего колебания А0 равна алгебраической сумме амплитуд складываемых колебаний. Если разность фаз складываемых колебаний, соответствующих краям щели равна p (т.е. разность хода D = ЕD = b sin j = l /2, рис.3), то векторы DА располагаются вдоль полуокружности длиной А0 (рис. 2, б). Следовательно, для результирующей амплитуды получим значение А = 2А0/p. В случае, когда D = b sin j = l, колебания от краев щели отличаются по фазе на 2p. Соответствующая векторная диаграмма дана на рис. 2, в. Векторы D А располагаются вдоль окружности длиной А0. Результирующая амплитуда равна нулю, что соответствует первому минимуму. Первый максимум наблюдается при D = b sin j = 3 l /2. В этом случае колебания от краев щели отличаются по фазе на 3p. Строя последовательно векторы DА, мы обойдем полтора раза окружность диаметра А1 = 2А0/(3p) (рис. 2, г).
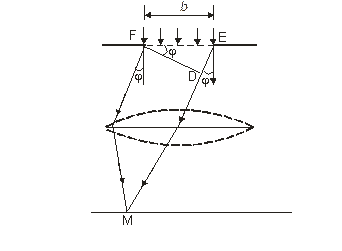
Рис. 3
Таким образом, амплитуда А 1 первого максимума составляет 2/(3 p) от амплитуды А 0 нулевого максимума, а интенсивность
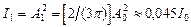 .
.
Аналогично можно найти и относительную интенсивность остальных максимумов.
В результате получаются следующие соотношения интенсивностей:
I 0 : I 1 : I 2 : I 3 :...: Im =
= 1:  :
:  :
:  :...:
:...:  =
=
= 1: 0,045: 0,016: 0,008:... (1)
Так как графический расчет является приближенным, то полученные соотношения также будут приближенными.
Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы. Ему соответствуют » 90% всего светового потока, выходящего из щели. Нетрудно видеть, что нулевая амплитуда будет соответствовать углам дифракции j k, при которых:
b sin jk = ± kl, (2)
где k = 1, 2, 3, … - порядок дифракционного минимума. Следовательно, (2) будет условием дифракционного минимума. При k =0, как видно, j0 = 0 и условие максимума нулевого порядка.
Условие дифракционного максимума выражается по формуле:
b sin j = ± (2 m +1) l/2.
График распределения интенсивности света на экране 3 показан на рис. 4. Вид дифракционной картины Фраунгофера зависит от ширины щели, а также от расстояния l от щели до экрана 3. Если, например, ширина щели b = l, то sin j 1 = 1, а следовательно, и j 1 = p /2, т.е. ни одного дифракционного минимума наблюдаться не будет, экран будет весь освещен: больше в центральной части и меньше к краям. Это соответствует чистой дифракции без интерференции. При малых углах дифракции картина может оказаться мелкой для наблюдения.

Рис. 4
В настоящей работе предлагается получить дифракционную картину от щели, произвести измерение интенсивности по длине дифракционной картины и построить экспериментальный график распределения относительной интенсивности.
Экспериментальная часть
Рабочая схема установки
Лабораторная установка собрана на прямолинейной оптической скамье лабораторного оптического комплекса ЛОК-1М (смотрите описание). Рабочая схема установки приведена на рис.5.

Рис. 5
Непрозрачный экран с прямоугольной щелью шириной 0,5 мм (№ 23) вставляется в держатель с кассетой для экранов (№ 8). Дифракционная картина возникает на экране Э2 , находящемся в объектной плоскости лупы Л2 (Д3). Лупа Л2 проецирует дифракционную картину на экран Э3 фоторегистратора ФР (Д4). Для получения четкой дифракционной картины между экраном со щелью и экраном Э2 помещают объектив (Д6). Изменяя расстояния между держателями, а также регулируя винты держателей добиваются четкой дифракционной картины на экране Э3 ФР так, чтобы при поперечном перемещении входное окошечко фотодатчика пересекало дифракционную картину. Для уменьшения светового потока, попадающего в фотодатчик, перед экраном со щелью помещают поляризатор (№ 11).
Порядок выполнения работы
| Упражнение 1. |
1. Получите на экране Э3 изображение дифракционной картины. Убедитесь, что центральный максимум дифракционной картины попадает в окошечко фотодатчика, находящееся в центре экрана Э3. Вращая ручку поляризатора, убедитесь, что освещенность на экране зависит от угла поворота плоскости поляризации.
2. Включите вольтметр. Поворачивая ручку поляризатора, добейтесь, чтобы показания вольтметра не превышали максимально допустимого значения (чтобы световой поток не насыщал фотоприемник).
3. Установите фотодатчик в центре дифракционной картины. Запишите показания милливольтметра U0. Перемещая фотодатчик вдоль дифракционной картины, через каждые 0,5 мм (пол-оборота барабана), снять показания вольтметра по всей длине дифракционной картины. Результаты занесите в таблицу.
U 0 = мВ
| № | х лев | U | 
| х прав | U | 
|
| ... |
4. Постройте график распределения относительной интенсивности в дифракционной картине I/I0 = f (x), считая, что показания вольтметра U пропорциональны интенсивности I. Сравните экспериментальные соотношения интенсивностей в дифракционных максимумах с теоретическими значениями (см. (1)).
5. Сделайте выводы.
| Упражнение 2. |
Получите дифракционную картину для 2-х, 3-х и 4-х щелей (№ 27, 29, 30). Сделайте сравнительный вывод.
Контрольные вопросы
1. Что понимают под явлением дифракции света?
2. Сформулировать принцип Гюйгенса-Френеля.
3. В чем состоит метод зон Френеля?
4. В чем различие между дифракцией Френеля и дифракцией Фраунгофера.
5. Получить условие дифракционного минимума для одной щели.
6. Получить условие дифракционного максимума для одной щели.
7. Нарисовать векторные диаграммы для разности фаз, складываемых колебаний, равной 0, p, 2 p.