МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра вычислительной техники и инженерной кибернетики
РЕКУРРЕНТНОЕ СУММИРОВАНИЕ РЯДОВ
Методикие указания по выполнению
лабораторной работы по программированию

Уфа – 2003
Целью работы является освоение методики разработки рекуррентных алгоритмов для вычисления бесконечных рядов, как по заданному числу членов, так и по заданной погрешности.
Теоретические вопросы
Повторить теоретические вопросы:
1. Понятие рекуррентного алгоритма.
2. Алгоритмы накопления сумм, произведений, факториалов.
3. Схема Горнера.
4. Понятие абсолютной и относительной погрешности.
Постановка задачи
Для ряда значений аргумента x от xн до xк с шагом dx вычислить сумму функционального ряда
S(x) = ∑ Fi(x), i=1,..,n (1)
а) с заданной точностью εz;
б) при заданном числе членов n= nz
Для проверки точности работы алгоритма (программы), т.е. в качестве контрольного примера используем значения функции
Y = f(X), (2)
которая аппроксимирует этот ряд.
Математическая справка
Рядом называется суммируемая последовательность членов
S = a1 + a2 + a3 +... +an +... (3)
В зависимости от числа членов ряд может быть конечным или бесконечным. Если членами ряда ai являются числа, то ряд называют числовым, а если функции Fi(x) некоторого аргумента x, то - функциональным. Если последовательность конечных сумм Sn числового ряда имеет при n → ∞ конечный предел, то ряд называют сходящимся (т.е. сумма бесконечного ряда - конечное число). Расходящиеся ряды практического применения не имеют.
Функциональные ряды при конкретном значении аргумента можно считать числовыми. Для функциональных рядов, при этом имеется понятие области сходимости - при некоторых значениях аргумента x ряд сходится, а при других, которые вне этой области, - ряд расходится. Функциональные ряды очень широко применяются как в самой математике, так и во многих инженерных науках для аппроксимации различных функций.
В частности, многие стандартные функции алгоритмических языков вычисляются по алгоритмам и программам, аналогичным данной работе. (Когда не было ЭВМ, люди пользовались таблицами алгебраических и специальных функций, рассчитанных по таким же алгоритмам). Например функция sin(x) может быть представлена следующим бесконечным рядом
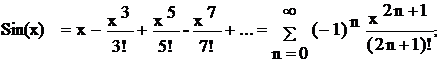 (1’)
(1’)
Поскольку, практически можно просуммировать лишь конечное число членов ряда, то при этом, естественно, будут погрешности. Могут быть два типа погрешностей: - погрешность округления εок и - погрешность усечения εус.
Погрешность округления зависит от точности представления чисел в ЭВМ (количества разрядов числа). Если к задаче не предъявляется специально повышенная точность, то при ее решении на современных ЭВМ погрешность округления редко принимают во внимание. За погрешность усечения εус принимают сумму отброшенных членов, называемую остатком ряда Qn:
│Qn │ ≤ εус (4)
По определению сумма бесконечного ряда состоит из частичной суммы Sn удерживаемых n членов и остатка Qn
S =Sn + Qn (5)
очевидно, что при n → ∞, Qn → 0.
При вычислении рядов всегда стоит проблема: сколько нужно удержать членов, чтобы погрешность не превысила заданную величину εz? Для этого существуют теоретические оценки:
а) если ряд знакочередующийся, то величина, остатка ряда Qn не превышает величины модуля первого отброшенного члена an+i, а тем более и последнего оставшегося члена
│Qn│ ≤ │an+1 │≤ │an │ (6)
б) если ряд знакопостоянный и монотонно убывающие его члены an = F(n) можно считать функцией непрерывного аргумента n, то
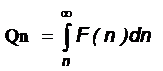 (7)
(7)
Вычисление погрешности Qn по формуле (7) значительно трудней, чем решение самой задачи (1). Поэтому мы и для знакопостоянных рядов погрешность будем определять в соответствии с (6).
Методические указания по решению задачи
Решение S задачи (1) как отмечалось, всегда будет приближенным, назовем его фактическим значением, а за истинное значение величины S будем принимать функцию Y(x), которая предназначена в качестве контрольного примера.
Оценку качества работы программы (алгоритма) будем осуществлять с помощью относительной погрешности
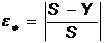 (8)
(8)
Из постановки задачи (1)-(2) ясно, что должен быть организован главный цикл изменения аргумента X. Внутри этого цикла должны выполняться следующие операции:
- рекуррентное накопление суммы ряда при текущем X;
- вычисление Y;
- оценка точности вычисления εф по формуле (8);
- печать строки таблицы результатов x, y, S, εф и εт