Рассмотренный выше универсальный алгоритм позволяет быстро и точно вычислять сумму ряда при заданном числе членов n. Однако он не рационален по затратам машинного времени, поскольку различные ряды имеют различную и неизвестную заранее скорость сходимости. Т.о., не зная заранее, какое число n надо брать, мы тратим впустую машинное время, которое имеет определенную стоимость. Более эффективным был бы алгоритм, который останавливался бы по мере достижения заданной точности (погрешности). Для оценки точности вычисления суммируемого ряда (1) нельзя использовать формулу (8), т.к. величина У дана нам в качестве контрольного примера и не будет известна в практических расчетах. (Собственно, разрабатываемый алгоритм и предназначен для вычисления этой функции У). Поскольку частичные суммы Si и Si-1 отличаются друг от друга на абсолютную величину текущего члена Fi, то для оценки текущей точности знакочередующихся рядов в соответствии с (6) можно использовать относительную величину
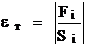, (15)
и, таким образом, оценка текущей точности будет формироваться автоматически в процессе суммирования ряда. Для знакопостоянных рядов из-за трудоемкости расчета интеграла (7), текущую погрешность eт также будем оценивать по формуле (15).
Таким образом, общий алгоритм решения задачи (1), (2) для варианта "по заданной точности" будет иметь вид
1. Печать головки таблицы " X, Y, S, eф eт n "
2. Цикл x= xн, xк, dx
3. S = Sнач: F = Fнач:
4. i = iнач// Циклпока
5. R=f(i, x)
6. F = F*R
7. S = S + F: i=i+1
8. Et=|F/S|
9. Если Et > Eз, то переход к пп. 5
10. y=f(x)
11. Eф = | (S-y)/S |
12. Печать значений x, У, S, Eф, Et, i
13. Конец по x
14. Конец алгоритма
Вариант алгоритма ”по заданному n” отличается в пп. 9 условием i < nз
При разработке программы можно совместить оба условия - e < eз и i < nз в одном цикле. В этом случае при счете исходным данным eз и nз надо задавать такие значения, чтобы алгоритм выходил из цикла по желаемому для нас варианту. Например, если хотим считать по nз, то его значение надо брать в соответствии с заданием, а погрешность eз - недостижимо малой, например, 0. И наоборот, если хотим, чтобы программа суммировала ряд по заданной точности eз, задаем разумную ее величину 10-3 или 10-4, а nз берем очень большое - 1000. Поскольку мы предусмотрели печать числа циклов i, то мы сможем оценить качество работы программы (сходимость алгоритма).
Указания по выполнению работы
Обратить внимание, что нам необходимо вычислять сумму ряда S и контрольных пример для нескольких значений аргумента x, т.е. будет еще один цикл.
Итак, мы разработали и отладили хорошую и полезную программу. Проведем теперь с ее помощью исследование рекуррентного алгоритма и свойств нашего ряда. Будем иметь в виду, что сходимость ряда (по числу членов при заданной точности) при различных значениях аргумента x может быть разной, а при некоторых x ряд даже может расходиться. В последнем случае потребуется отыскивать другой диапазон xн, xк значений аргумента.
Упражнение 1. Расчет суммы по заданному числу членов ряда. Прогнать программу при нескольких заданных значениях nз = 3, 4, 5 и диапазонах x (xн, xк) и проанализировать результаты этих расчетов.
Это позволит выбрать найти диапазон изменения x, в котором ряд S достаточно хорошо аппроксимирует функцию У.
Упражнение 2. Расчет суммы ряда по заданной погрешности. Реализовать второй вариант программы и прогнать ее при заданных значениях точности eз = 0.001, 0.0001. При этом обратить внимание: сколько членов потребуется для каждого значения eз и достигаются ли фактически заданные значения eз,
Обсудим полученные результаты.
Анализ полученных результатов.
В соответствии с заданием мы разработали алгоритм и программу рекуррентного суммирования функционального ряда (1), аппроксимирующего тригонометрическую функцию Sin(x). Программа была разработана по универсальному алгоритму, позволяющему выполнять расчеты суммы S как по заданному числу n, так и по заданной точности Eз.
Работоспособность алгоритма проверена с помощью таблицы прокрутки.
Используя нашу программу мы исследовали сходимость функционального ряда S к функции Y в диапазоне значений аргумента. x от 1 до 5.
Результаты расчетов по заданному числу членов n = 3, 4 и 5 приведены в табл. 1 при указанных значениях n. Как показали расчеты при значениях X от 0 до 1 уже при n =3 величина погрешности не превышает 0.00012.(Расхождения между значениями S и контрольным примером Y выделены шрифтом.)Поэтому на участке 0...1 графики всех функций практически совпадают. С увеличением значений Х возникают отклонения Sn=Sn(x) от функции Sin(x)
Таблица 1
Результаты численного эксперимента по исследованию сходимости ряда S (X)
xn= 0.1 xk= 0.9 dx= 0.2 ez=0.0 n=3
X Y S et ef n
0.10 0.099833 0.099833 0.00000083 0.00000007 3
0.30 0.295520 0.295520 0.00006852 0.00000010 3
0.50 0.47942 6 0.47942 7 0.00054318 0.00000317 3
0.70 0.6442 18 0.6442 34 0.00217403 0.00002526 3
0.90 0.783 327 0.783 421 0.00628111 0.00011969 3
для значений X от 2 до 5 трех членов явно не хватает, т.к. погрешности недопустимо велики
X Y S et ef n примеч
2.00 0.9 09297 0.9 33333 0.28571433 0.02643345 3 плохо
3.00 0. 141120 0. 525000 3.85714364 2.72023702 3 плохо
4.00 -0. 7568021.866667 4.57142830 3.46651769 3 оч плохо
5.00 -0. 95892410.208332 2.55102038 11.64560795 3 оч плохо
При n = 4 и 5 погрешности et и ef очень существенно уменьшаются до 10-4 и 10-6
X Y S et ef n
0.10 0.099833 0.099833 0.00000000 0.00000007 4
0.30 0.295520 0.295520 0.00000015 0.00000000 4
0.50 0.479426 0.479426 0.00000323 0.00000006 4
0.70 0.644218 0.644218 0.00002536 0.00000009 4
0.90 0.78332 7 0.78332 6 0.00012115 0.00000145 4
0.10 0.099833 0.099833 0.00000000 0.00000007 5
0.30 0.295520 0.295520 0.00000000 0.00000000 5
0.50 0.479426 0.479426 0.00000001 0.00000006 5
0.70 0.644218 0.644218 0.00000017 0.00000009 5
0.90 0.783327 0.783327 0.00000136 0.00000008 5
При n = 10 погрешности малы и для больших значений X вплоть до X =6, после чего точность снова снижается
X Y S et ef n примеч
1.00 0.841471 0.841471 0.00000000 0.00000000 10
2.00 0.909297 0.909297 0.00000000 0.00000000 10
3.00 0.141120 0.141120 0.00000007 0.00000095 10
4.00 -0.75680 2 -0.75680 3 0.00000299 0.00000032 10
5.00 -0.9589 24 -0.9589 34 0.00016351 0.00000976 10
6.00 -0.279 415 -0.279 818 0.01790207 0.00144140 10
7.00 0.6 56987 0.6 47033 0.14482442 0.01515059 10 плохо
8.00 0. 989358 0. 829417 1.42837524 0.16166174 10 оч плохо
Из полученных результатов можно сделать очевидный вывод: чем больше n тем программа точнее считает, но в ограниченном диапазоне X. Для больших X требуется больше n.
В упражнении 2 мы вычисляли сумму ряда по заданной погрешности eз = 0.001 и 0.0001 для разных диапазонов аргумента X и получили следующие результаты
Таблица 2. Результаты расчетов по заданной точности (погрешности eз= 10-3)
X Y S et ef n примеч
0.10 0.099833 0.099833 0.00000083 0.00000007 2
0.30 0.295520 0.295520 0.00006852 0.00000010 2
0.50 0.47942 6 0.47942 7 0.00054318 0.00000317 2
0.70 0.644218 0.644218 0.00002536 0.00000009 3
0.90 0.78332 7 0.78332 6 0.00012115 0.00000145 3
1.00 0.8414 71 0.8414 68 0.00023579 0.00000326 3
2.00 0.90929 7 0.90929 6 0.00005642 0.00000144 5
3.00 0.141120 0.141120 0.00007776 0.00000338 7
4.00 -0.75680 2 -0.75680 0 0.00006382 0.00000268 8
5.00 -0.9589 24 -0.9589 34 0.00016351 0.00000976 9
6.00 -0.27941 5 -0.27941 9 0.00010933 0.00001408 11
7.00 0.6569 87 0.6569 93 0.00013160 0.00000980 12
8.00 0.9893 58 0.9893 25 0.00022444 0.00003332 13
9.00 0.4121 18 0.4121 22 0.00011258 0.00000853 15
10.00 -0.5440 21 -0.5440 32 0.00021168 0.00001994 16
12.00 -0.536 573 -0.536 051 0.00011202 0.00097232 19
14.00 0.9 90607 0.9 86741 0.00032222 0.00390291 21 плохо
16.00 -0. 287903 -0. 312782 0.00052788 0.08641405 24 оч плохо
18.00 - 0.750987 - 1.016769 0.00077857 0.35391021 26 оч плохо
20.00 0.9129452.213388 0.00018780 1.42444754 29 оч плохо
При ez = 10-4 программа работает точнее и обеспечивает условие et< 10-4.
6.00 -0.27941 5 -0.27941 8 0.00000656 0.00000747 12
8.00 0.9893 58 0.9893 43 0.00001769 0.00001560 14
10.00 -0.5440 21 -0.5440 42 0.00001779 0.00003769 17
12.00 -0.536 573 -0.536 046 0.00000984 0.00098209 20
14.00 0.9 90607 0.9 86773 0.00003190 0.00387114 22 плохо
16.00 -0. 287903 -0. 312799 0.00005299 0.08647160 25 плохо
При ez = 10-5 также обеспечивается условие et< 10-5
X Y S et ef n примеч
4.00 -0.75680 2 -0.75680 3 0.00000299 0.00000032 9
6.00 -0.27941 5 -0.27941 8 0.00000656 0.00000747 12
8.00 0.9893 58 0.9893 42 0.00000122 0.00001681 15
10.00 -0.5440 21 -0.5440 41 0.00000134 0.00003637 18
12.00 -0.536 573 -0.536 046 0.00000984 0.00098209 20
14.00 0.9 90607 0.9 86770 0.00000289 0.00387403 23 плохо
16.00 -0. 287903 -0. 312797 0.00000492 0.08646622 26 плохо
Как видно из таблицы при любых значения X наша программа обеспечивает условие Et < Eз (точность не хуже заданной), хотя при больших X (>14) ей не удается обеспечить приемлемую фактическую погрешность ef. При этом, для обеспечения заданного условия программе с ростом X требуется увеличивать n.
(При малых значениях X (< 14) наша программа работает лучшее чем библиотечная функция Sin(x), а при больших X (>14) – хуже. Одна из причин: все библиотечные программы работают с данными двойной точности double, а наша - с обычной – float. Объяснение второй причины см. в приложении 1)
Вывод: при любых значениях X (< 14) наша программа обеспечивает расчет Sin(x) с точностью не хуже заданной величины Eз.
Опыт 3. Двойная точность. Заменив в нашей программе тип данных для переменных S, F, R et, ef на double, убеждаемся, что теперь и для больших X (до 30) наша программа работает не хуже библиотечной Sin(x)
Теперь, при двойной точности, при ez = 10-4 обеспечивается ef< 10-4 для X< 30
X Y S et ef n
16.00 -0.28790 3 -0.28790 5 0.00005757 0.00000495 25
18.00 -0.75098 7 -0.75098 6 0.00001167 0.00000099 28
20.00 0.91294 5 0.91294 9 0.00004976 0.00000463 30
а при ez = 10-5 обеспечивается ef< 10-5 для X< 30,
X Y S et ef n примеч
30.00 -0.9880 32 -0.9880 04 0.00000196 0.00002811 45
32.00 0.5514 27 0.5514 59 0.00000188 0.00005933 48
34.00 0.5 29083 0.5 33275 0.00000951 0.00792360 50 плохо
36.00 -0.9 91779 -0.9 46517 0.00000288 0.04563676 53 плохо
38.00 0. 296369 0. 604222 0.00000243 1.03875314 56 плохо
Таким образом, в результате выполненной работы и проведенных исследований можно сделать следующие выводы:
1. Мы научились разрабатывать рекурреные алгоритмы и программы вычисления рядов (бесконечных сумм) по заданной погрешности.
2. При разработке рекуррентых алгоритмов очень удобно использовать таблицу прокрутки, которая гарантирует правильность работы будущей программы.
3. Разработанные нами алгоритм и программа не только работоспособны, но и очень эффективны. Позволяют очень точно вычислять функцию Sin(x) для широкого диапазона значений аргумента X.
4. Мы убедились, что наша программа более эффективно (точнее и быстрее) вычисляет значения функции Sin(x) с помощью ряда (1) в области главных значений аргумента от - π/2 до + π/2.
5. ЭВМ можно использовать для получения новых знаний путем проведения вычислительных экспериментов.