Прогрессии арифметические

3.1.1 Арифметическая прогрессия обладает следующим свойством: при любом сумма её первых членов равна . Найти разность этой прогрессии и три первых её члена.

3.1.2 Известно, что при любом сумма членов некоторой арифметической прогрессии выражается формулой . Найти три первых члена этой прогрессии.

3.1.3 Сумма первых трёх членов возрастающей арифметической прогрессии равна 15. Если от первых двух членов этой прогрессии отнять по 1, а к третьему члену прибавить 1, то полученные три числа составят геометрическую прогрессию. Найти сумму 10 первых членов арифметической прогрессии.

3.1.4 Сумма третьего и девятого членов арифметической прогрессии равна 8. Найти сумму 11 первых членов этой прогрессии.

3.1.5 Сумма трёх чисел, образующих арифметическую прогрессию, равна 2, а сумма квадратов этих же чисел равна . Найти эти числа.

3.1.6 Найти третий член бесконечной геометрической прогрессии со знаменателем , сумма которой равна , второй член равен .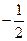

3.1.7 Доказать, что если числа , и составляют арифметическую прогрессию, то числа , и в указанном порядке составляют также арифметическую прогрессию.

3.1.8 Найти сумму всех трёхзначных чисел, делящихся на 7.

3.1.9 Найти сумму всех трёхзначных чисел, делящихся на 3.

3.1.10 Найти целое положительное число из уравнения .

3.1.11 Три числа составляют геометрическую прогрессию. Если от третьего отнять 4, то числа составят арифметическую прогрессию. Если же от второго и третьего членов полученной арифметической прогрессии отнять по 1, то снова получится геометрическая прогрессия. Найти эти числа.

3.1.12 Даны две арифметические прогрессии. Первый и пятый члены первой прогрессии равны соответственно 7 и -5. У второй прогрессии первый член равен 0, а последний член равен . Найти сумму членов второй прогрессии, если известно, что третьи члены обеих прогрессий равны между собой.

3.1.13 Известно, что в некоторую арифметическую прогрессию входят члены и такие, что . Имеется ли член этой прогрессии, равный нулю? Если да, то каков номер этого члена.

3.1.14 Доказать, что любой член арифметической прогрессии, начиная со второго, есть среднее арифметическое между двумя любыми членами, равноудалёнными от него.

3.1.15 От деления тринадцатого члена арифметической прогрессии на третий член в частном получается 3, а от деления восемнадцатого члена на седьмой член получается 2 и в остатке 8. Определить разность и первый член прогрессии.

3.1.16 Найти три первых члена арифметической прогрессии, у которой сумма любого числа членов равна утроенному квадрату этого числа.

3.1.17 Найти сумму всех положительных двузначных чисел, делящихся на 3 нацело.

3.1.18 Первый член арифметической прогрессии равен 429, разность её равна -22. Сколько членов этой прогрессии нужно взять, чтобы их сумма была равна 3069?

3.1.19 Арифметическая прогрессия обладает следующим свойством: при любом сумма её первых членов равна . Найти разность этой прогрессии и три первых её члена.

3.1.20 Известно, что при любом сумма членов некоторой арифметической прогрессии выражается формулой . Найти три первых члена этой прогрессии.

3.1.21 Сумма первых трёх членов возрастающей арифметической прогрессии равна 15. Если от первых двух членов этой прогрессии отнять по 1, а к третьему члену прибавить 1, то полученные три числа составят геометрическую прогрессию. Найти сумму 10 первых членов арифметической прогрессии.

3.1.22 Сумма третьего и девятого членов арифметической прогрессии равна 8. Найти сумму 11 первых членов этой прогрессии.

3.1.23 Сумма трёх чисел, образующих арифметическую прогрессию, равна 2, а сумма квадратов этих же чисел равна . Найти эти числа.

3.1.24. Найти натуральные числа, образующие арифметическую прогрессию, если произведения трёх и четырёх первых её членов равны соответственно 6 и 24.

3.1.25 Найти третий член бесконечной геометрической прогрессии со знаменателем , сумма которой равна , второй член равен .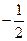

3.1.26 Сумма третьего и девятого членов арифметической прогрессии равна 6, а их произведение равно . Найти сумму 15 первых членов этой прогрессии.

3.1.27 При делении девятого члена арифметической прогрессии на второй член в частном получается 5, а при делении тринадцатого члена на шестой член в частном получается 2 и в остатке 5. Найти первый член и разность прогрессии.

3.1.28 Турист, поднимаясь в гору, в первый час достиг высоты 800 м, а каждый следующий час поднимался на высоту, на 25 м меньшую, чем в предыдущий. За сколько часов он достигнет высоты в 5700 м?

3.1.29 Найти число членов арифметической прогрессии, у которой сумма всех членов рана 112, произведение второго члена на разность прогрессии равно 30, а сумма третьего и пятого членов равна 32. Написать три первых члена этой прогрессии.

3.1.30 Найти три первых члена , , арифметической прогрессии, если известно, что , и .

3.1.31 В соревновании по стрельбе за каждый промах в серии из 25 выстрелов

стрелок получал штрафные очки: за первый промах – одно штрафное очко, а за каждый последующий – на очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков.

3.1.32 Сумма первого и пятого членов арифметической прогрессии равна , а произведение третьего и четвёртого её членов равно . Найти сумму 17 первых членов этой прогрессии.

3.1.33 За изготовление и установку самого нижнего железобетонного кольца колодца заплатили 26 руб, а за каждое следующее – на 2 руб меньше, чем за предыдущее. Кроме того, по окончании работы было уплачено ещё 40 руб.