Типовые звенья и их временные и частотные характеристики

Для исследования процессов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближённо характеризуют реальные звенья систем в заданном диапазоне частот. Рассматривая характеристики звеньев вне зависимости от их назначения, физического принципа действия, мощности и скорости передаваемых сигналов, можно выделить ряд типовых (элементарных) звеньев, описываемых обыкновенными дифференциальными уравнениями первого и второго порядка.

Все типовые звенья имеют передаточную функцию, которая представляет собой рациональную дробь.

Сложные линейные звенья могут быть сведены к соединению типовых, порядок дифференцирования которых не выше второго. Из курса алгебры известно, что полином любого порядка может быть разложен на простые сомножители, поэтому произвольную дробно-рациональную функцию всегда можно представить в виде произведения простых дробей.

Звенья, передаточные функции которых имеют вид простых множителей или простых дробей, называют типовыми (элементарными).

Типовые звенья делят на:

· простейшие (пропорциональное, интегрирующее, дифференцирующее);

· звенья первого порядка (апериодическое, форсирующее);

· звенья второго порядка.

Простейшие звенья

Пропорциональное (безинерционное) звено.

Звено, выходная величина которого прямо пропорциональна входной величине, называется пропорциональным и описывается уравнением вида .

Примером такого звена являются делитель напряжения, рычажная передача, редукторная передача, усилитель постоянного тока.

Изображение выходного сигнала .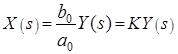

Передаточная функция .

ИПФ: ПХ: .

Рис. 1 Рис. 2

Частотные характеристики: ; (рис 3);

АЧХ: (рис. 4); ФЧХ: (рис. 5)

ЛАЧХ: .

Рис.3 АФЧХ Рис.4 АЧХ Рис 5 ФЧХ

Интегрирующее звено.

Звено, выходная величина которого пропорциональна или равна интегралу по времени от входной величины, называется интегрирующим и описывается уравнением вида или , где .

Изображение выходного сигнала имеет вид: .

Передаточная функция звена .

ИПФ: ПХ:

Графики приведены на рис. 7 и 8.

Рис.7. ИПФ интегрирующего звена

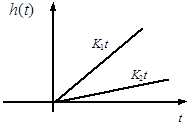
Рис. 8. ПХ интегрирующего звена

,

где .

 

 

Рис.9. АФЧХ интегрирующего звена

 

При изменении частоты от 0 до конец вектора движется по отрицательной части мнимой оси от до 0.

Интегрирующее звено создает отставание выходного гармонического сигнала на 90° на всех частотах; амплитуда выходного сигнала уменьшается с возрастанием частоты рис. 10.

АЧХ: ; .

ФЧХ: .

Рис. 10. АЧХ и ФЧХ интегрирующего звена.

Логарифмическая частотная характеристика имеет вид: .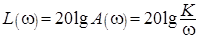

Зависимость — прямая линия с наклоном -20 дб/дек (Рис.11).

Пусть , К=100, тогда .

Пусть 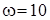, тогда .

Пусть 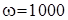, тогда .

Из этого рисунка видно, что при изменении частоты на одну декаду значение ЛАЧХ изменится на –20 дб. Следовательно, она имеет вид прямой.

 

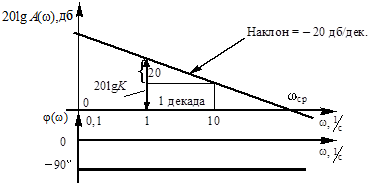
Рис. 11. ЛАЧХ и ЛФЧХ интегрирующего звена

Дифференцирующее звено.

Звено, выходная величина которого пропорциональна или равна производной по времени от входной величины, называется идеальным дифференцирующим и описывается уравнением вида , где .

Передаточная функция имеет вид .

Импульсная переходная функция и переходная характеристика определяются зависимостями .

Частотные характеристики выражаются формулами:

.

АЧХ и ФЧХ изображены на рис. 12.

Рис. 12. Частотные характеристики дифференцирующего звена

Логарифмическая амплитудно-частотная характеристика имеет вид:

.

Пусть , К=10, тогда .

Пусть 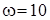, тогда .

Зависимость — прямая линия с наклоном +20 дб/дек (Рис.13).

увеличивается на 20 дб при увеличении частоты на одну декаду.

Рис. 13. Логарифмические характеристики дифференцирующего звена

Звенья первого порядка

Апериодическое (инерционное) звено 1 порядка.

Дифференциальное уравнение имеет вид: .

Получим передаточную функцию: .

.

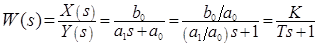Величины и соответственно называются коэффициентом усиления и постоянной времени апериодического звена.

Коэффициент характеризует уровень изменения выходного сигнала, постоянная времени характеризует инерционные свойства системы, т.е. как быстро система отрабатывает поступившее воздействие.По известным формулам или таблице оригиналов и изображений получим зависимости, определяющие ИПФ и ПХ:

(рис.15).

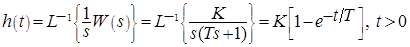(рис.16).

.

Рис.15 ИПФ апериодического звена

Рис. 16. ПХ апериодического звена

 

Преобразование Лапласа при ненулевых начальных условиях имеет вид: ;

.

.

Найдем частотные характеристики:

В теории управления часто используется метод качественного построения частотных характеристик по контрольным точкам (рис.17).

; .

По полученным контрольным точкам легко построить годограф .

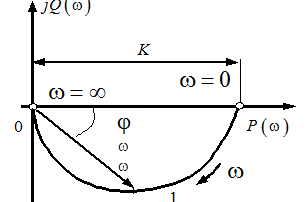
Рис. 17. АФЧХ апериодического звена

, тогда

.

ФЧХ определяется формулой .

.

Графики и изображены на рис.18.

Рис. 18. АЧХ и ФЧХ апериодического звена

Логарифмические амплитудные характеристики пропорционального, интегрирующего и дифференцирующего звеньев являются прямыми, и их легко построить. Построение ЛАЧХ других элементарных звеньев требует дополнительных вычислений и построений. Поэтому на практике часто ограничиваются построением приближённых асимптотических ЛАЧХ.

ЛАЧХ апериодического звена определятся формулой:

.

Рассмотрим две области построения:

1. , тогда .

На частотах в выражении пренебрегают слагаемым и характеристика в этой области представляет собой прямую, параллельную оси абсцисс.

2. , тогда .

На частотах в выражении пренебрегают единицей и характеристика в этой области представляет собой прямую с наклоном -20 дб/дек.

Асимптотическая ЛАЧХ апериодического звена представлена (рис.19).

Рис. 19. Приближенная (асимптотическая) ЛАЧХ апериодического звена.

Частоты, на которой асимптотические ЛАЧХ претерпевает излом, называют сопрягающими частотами. Определим значение функции на этой частоте.

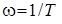
, где .

Это говорит о том, что на частоте сопряжения точная ЛАЧХ будет меньше на три дБ, относительно асимптотической.

 

Рис. 20. ЛАЧХ и ЛФЧХ апериодического звена

Дифференцирующее звено первого порядка (форсирующее).

Дифференциальное уравнение имеет вид: .

Получим передаточную функцию: .

.

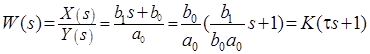Величины и соответственно называются коэффициентом усиления и постоянной времени форсирующего звена.

;

 

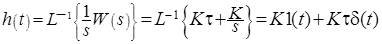
Частотные характеристики:

.

.

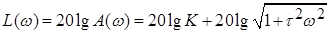Построение асимптотической ЛАЧХ форсирующего звена аналогичен построению ЛАЧХ интегрирующего звена.

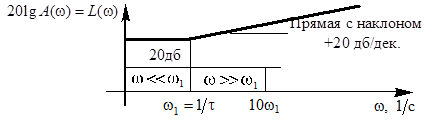
Рис.21 Асимптотическая ЛАЧХ дифференцирующего звена

Звенья второго порядка

Колебательное звено. Имеем уравнение .

Примеры звеньев приведены на рис. 22.

Рис. 22. Примеры колебательных звеньев:
а - RLC -колебательный контур; б - механическая система (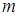 - масса, - коэффициент упругости пружины, - коэффициент демпфирования)

Найдем ПФ. Имеем

Тогда

где или (при ).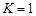

Параметры 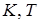и называются коэффициентом усиления, постоянной времени и коэффициентом демпфирования (колебательности) колебательного звена соответственно.

При различных значениях имеют место следующие звенья:

· —консервативное или вырожденное колебательное (корни чисто мнимые);

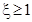· — апериодическое 2-го порядка (корни вещественные);

· — колебательное корни комплексно-сопряжённые).

Рассмотрим колебательное звено.

Найдём корни характеристического уравнения .

, где

- частота собственных колебаний звена,

- сопрягающая частота системы.

Вещественная часть корня представляет собой коэффициент затухания переходного процесса; мнимая часть корня – частоту колебаний переходного процесса.

Для получения временных характеристик можно воспользоваться таблицей оригиналов и изображений или соответствующей аналитической формулой.

Запишем выражение для ИПФ колебательного звена (рис. 23).

.

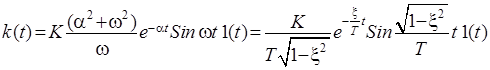Перед построением ИПФ определим начальные и конечные значения:

Рис. 23. ИПФ колебательного звена ()

Определим переходную функцию колебательного звена (рис. 24).

Перед построением переходной функции определим начальные и конечные значения:

Рис. 24. Переходная характеристика колебательного звена

при различных значениях

Перейдем к рассмотрению частотных характеристик.

АФЧХ колебательного звена представлены на рис. 25.

Рис. 25. АФЧХ колебательного звена.

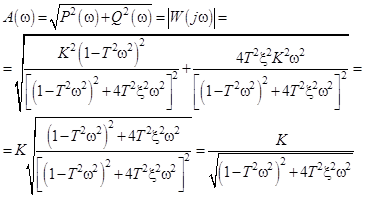
Определим значение АЧХ в контрольных точках:

Амплитудная характеристика плавно уменьшается, если . Если , то на амплитудной характеристике появляется резонансный «горб».

Частота, при которой амплитудная характеристика достигает максимального значения, называется резонансной и определяется формулой

.

Частота как в случае апериодического звена, так и в случае колебательного звена называется сопрягающей частотой.

ФЧХ имеет вид

Определим значение ФЧХ в контрольных точках:

Графики и изображены на рис. 26.

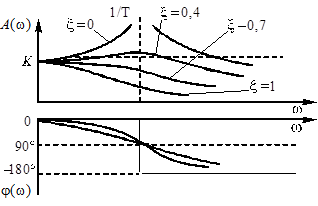
Рис. 26. АЧХ и ФЧХ колебательного звена для различных значений .

Построим асимптотическую ЛАЧХ:

1. Пусть , тогда в выражении пренебрегают вторым слагаемым и и характеристика в этой области представляет собой прямую, параллельную оси абсцисс.

2. Если , то в выражении во втором слагаемом оставляют только наибольшее слагаемое , тогда .

Характеристика в этой области представляет собой прямую с наклоном -40 дб/дек.

Определим значение функции на частоте сопряжения

На рис. 27 и 28 показаны асимптотическая ЛАЧХ и ЛФЧХ колебательного звена для различных значений .

Рис. 27. ЛАЧХ колебательного звена при различных значениях

Рис. 28. ЛФЧХ колебательного звена при различных значениях

Рассматривая колебательное звено в общем виде, мы получаем в качестве частных случаев ещё 2 типовых звена: консервативное и апериодическое второго порядка.

.

Есть звенья, которые традиционно относятся к типовым и указываются в таблицах, но при этом они не являются простейшими.К ним относятся:

-интегрирующеес замедлением или инерционное интегрирующее;

- дифференцирующее с замедлением (инерционное дифференцирующее);

- интегро- дифференцирующее, если , то звено ближе к интегрирующему; если , то звено ближе к дифференцирующему.

Неминимально – фазовые звенья.

Важным общим показателем типовых звеньев является принадлежность нулей передаточной функции к левой полуплоскости комплексного переменного.

Пусть имеем: , где

- полюса знаменателя; -нули числителя. Рассмотрим один из сомножителей знаменателя . Звенья, нули и полюса которых лежат в левой полуплоскости, называют минимально-фазовыми. Звенья, передаточные функции которых имеют нули и полюса, лежащие в правой полуплоскости, называются неминимально-фазовыми.