Преобразование Лапласа.
Пусть задана функция вещественного переменного 
, определённая при 
. Функция, которая подвергается преобразованию Лапласа, должна обладать следующими свойствами:
1. функция должна быть определена и дифференцируема по всей положительной полуоси;
2. функция должна быть тождественно равна 0 при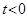 
, т.е. (
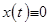при );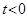
3. функция должна быть ограниченна, т.е. для функции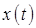 
существуют такие положительные числа М и с, что 
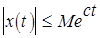при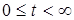 
, т.е.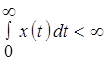 
, где с – абсцисса абсолютной сходимости (некоторое положительное число).
Т.о. для некоторой кусочно-непрерывной функции 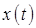, возрастающей при 
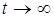не быстрее чем 
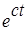, может быть поставлено в соответствие её преобразование Лапласа.
Преобразованием Лапласа называют соотношение вида 
,
ставящее функции 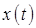вещественного переменного 
в соответствие функцию 
комплексного переменного 
(
).
При этом 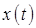называется оригиналом, 
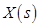– изображением, для обозначения соответствия между изображением и оригиналом используют знак соответствия «
».
Используется также символическая запись преобразования Лапласа, а именно,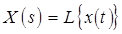 
, где 
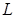– оператор прямого преобразования Лапласа, 
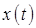- образ функции является функцией комплексного переменного 
, определяемой при 
.
Если функция тождественно равна 0 при 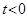, то 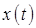может быть однозначно определена (с точностью до значений в точках разрыва) по своему 
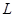- образу, т.е. 
, где 
- оператор обратного преобразования Лапласа.
Рассмотрим несколько примеров:
1. 
; 
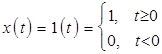
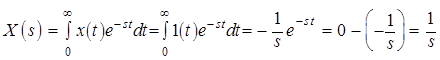2. 
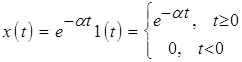
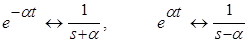
3. 
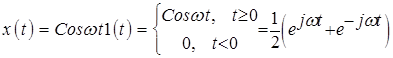
Преобразование Лапласа обладает следующими свойствами:
· Линейности:
если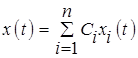 
, то 
, где 
· Изменения масштаба во временной области:
если 
то 
.
· Смещения аргумента в области изображения (комплексной области):
пусть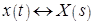 
, тогда 
· Смещения аргумента в области оригинала (вещественной области):
пусть 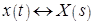, тогда 
· Дифференцирования оригинала:
при ненулевых начальных условиях 
при нулевых начальных условиях 
.
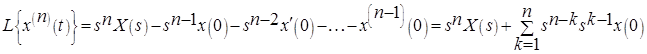
· Интегрирования оригинала при нулевых начальных условиях:
.
· Свертки функций в действительной области:
.
О предельных значениях:
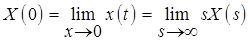- теорема о начальном значении
- теорема о конечном значении.
Комплексная передаточная функция
Вернёмся к записи дифференциального уравнения в виде
Пусть функци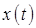и и 
являются непрерывными, дифференцируемыми, ограниченными и тождественно равными 0 при 
. Применим преобразование Лапласа при нулевых начальных условиях и получим
Обозначим: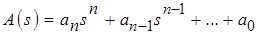 
,
.
, где
- обычные функции комплексного переменного.
Изображение выходного сигнала системы имеет вид:
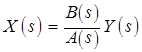или 
.
Передаточной функцией в изображениях по Лапласу (ПФ) системы называется отношение изображения по Лапласу выходного сигнала 
к изображению по Лапласа входного сигнала 
при нулевых начальных условиях.
Комплексная передаточная функция преобразования «вход–выход» системы может быть получена заменой символа дифференцирования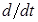 
(или оператора дифференцирования) на комплексную переменную 
.
Передаточная функция представляет собой дробно-рациональную функцию, причем в реальной системе порядок числителя 
не превышает порядка знаменателя 
, т.е. 
. Коэффициенты передаточной функции 
вещественны, поскольку они представляют собой функции от вещественных параметров системы.
Значения , при которых ПФ обращается в нуль, называются нулями ПФ. Нули являются корнями уравнения
.
Значения , при которых ПФ обращается в бесконечность, называются полюсами ПФ. Полюсы являются корнями уравнения
.
Передаточная функция 
имеет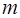 
нулей и 
полюсов. Нули и полюса могут быть действительными или комплексно-сопряженными, поэтому их можно изобразить на комплексной плоскости (s -плоскости).
Нули и полюса называются левыми (правыми), если они расположены в левой (правой) части s-плоскости, и нейтральными или нулевыми, если они лежат соответственно на мнимой оси или в начале координат.