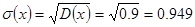Задание № 1. Найти производную
; 
; 
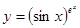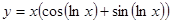
Решение:
производная сложной функции
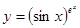
Прологарифмируем обе части, а затем найдём производную
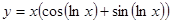
Задание № 2. Найти пределы функций
; 
; 
; 
Решение:
для раскрытия неопределённости разделим числитель и знаменатель на 
для раскрытия неопределённости умножим и числитель и знаменатель на сопряжённое
для раскрытия неопределённости числитель представим в виде произведения
Задание № 3. Провести полное исследование функции и построить ее график
Решение:
1. Область определения функции: функция не определена при x =1. Область определения состоит из двух интервалов 
, а график из двух ветвей.
. Функция нечетная, ни нечётная
. Точки пересечения графика с осями координат: если x =0, то 
точка пересечения О (0;-1)
4. Прямая x =1 является вертикальной асимптотой.
,
значит x =1 точки разрыва 2го рода.
Проверим наличие наклонной асимптоты в виде y=kx+b, где
производный функция экстремум график
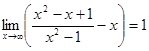
Значит, y=x+1 наклонная асимптота
5. Найдём интервалы возрастания и убывания функции и её экстремумы.
при 
, 
Исследуем критическую точку x =0
, значит функция возрастающая на интервале 
.
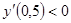, значит функция убывающая на интервале 
.
Следовательно, точка максимума, а максимум функции 
Итак, О (0;0) - максимум
Кроме того, 
, значит функция возрастающая на интервале 
.
Следовательно, точка минимума, а минимум функции 
Итак, О (2;3) - минимум
6. Найдём интервалы выпуклости вверх и выпуклости вниз; определим точки перегиба.
и не существует при 
функция выпукла вверх на интервале 
функция выпукла вниз на интервале 
Функция не существует в точке перегиба.
7. Построим график функции, используя полученные данные.
Задание № 4. Решить дифференциальные уравнения
; 
Решение:
Имеем дифференциальные уравнения с разделяющимися переменными. Разделим переменные, а затем проинтегрируем обе части
Задание № 5. Решить задачу
) В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по-английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислите вероятность того, что из членов группы в первом отеле:
а) все туристы говорят хорошо по-английски;
б). Только один турист хорошо говорит по-английски.
Решение:
a) общее число элементарных исходов равно числу способов, которыми можно выбрать три туриста из 15, т.е.
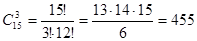
число исходов, благоприятствующих событию, равно числу способов выбрать троих из 5 хорошо говорящих, т.е.
Искомая вероятность того, что из членов группы в первом отеле все туристы говорят хорошо по-английски:
б) Только один турист хорошо говорит по-английски.
общее число элементарных исходов равно числу способов, которыми можно выбрать три туриста из 15, т.е.
число исходов, благоприятствующих событию, равно числу способов выбрать одного из 5 хорошо говорящих, т.е. 
и при этом остальные двое не должны хорошо говорить по-английски, число способов
Искомая вероятность того, что из членов группы в первом отеле только один турист говорит хорошо по-английски:
2) Дискретная случайная величина распределена по закону:
| Х | -1 | ||
| p | 0,3 | 0,6 | 0,15 |
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение
Решение:
Математическое ожидание:
Дисперсия:
среднее квадратичное отклонение:
