Введение
Информатика, как никакая другая область знаний, характеризуется чрезвычайно высокой степенью динамики изменений. Кроме того, учитывая ее всепроникающий характер, благодаря которому происходят интеграция знаний, идей, в настоящее время трудно очертить границы информатики.
Информатика и связанные с ней информационные технологии – необходимый атрибут профессиональной пригодности в обществе.
Информатика служит, прежде всего, для формирования определенного мировоззрения в информационной сфере и освоение информационной культуры, т.е. умение целенаправленно работать с информацией, профессионально используя ее для получения, обработки и передачи компьютерную информационную технологию и соответствующие ей технические и программные средства.
Информатизация обеспечит переход общества от индустриального этапа развития к информационному. Информационный рынок предоставит потребителям все необходимые информационные продукты и услуги, а их производство обеспечит индустрии информатики, часто называемая информационной индустрией. Все эти вопросы сейчас активно обсуждаются в печати, хотя до сих пор нет единого мнения относительно времени путей развития, понимания приоритетности того или иного направления, формулировок и понятий и т.п.
Целью контрольной работы является изучение логических основ работы ЭВМ, основных понятий и операций алгебры логики, а также прикладного программного обеспечения.
Логические основыЭВМ. Основные законы алгебры логики
Алгебра логики
Кроме обычной алгебры существует специальная, основы которой были заложены английским математиком XIX века Дж. Булем. Эта алгебра занимается так называемым исчислением высказываний.
Ее особенностью является применимость для описания работы так называемых дискретных устройств, к числу которых принадлежит целый класс устройств автоматики и вычислительной техники.
При этом сама алгебра выступает в качестве модели устройства. Это означает, что работа произвольного устройства указанного типа может быть лишь в каком+то отношении описана с помощью построений этой алгебры. Действительное реальное устройство физически работает не так, как это описывает алгебра логики. Однако применение положений этой теории позволяет сделать ряд полезных в практическом отношении обобщений.
Рассмотрим некоторую схему и представим ее в виде так называемого "черного" ящика.
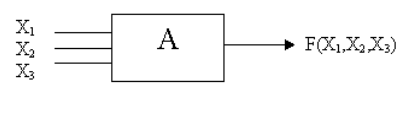
Будем считать, что внутреннее содержимое ящика неизвестно.
X1,X2,X3
– входные сигналы, F – выходной сигнал.
Считаем также, что схема А – элементарная, т.е. нет другой схемы Б, меньшей, чем А, которая бы содержалась в А.
Построим абстрактное устройство из элементарных устройств, типа А, Б, В и т.д. Очевидно, более сложное устройство можно построить из простых путем:
1. последовательного соединения элементов;
2. параллельного соединения;
3. перестановки входов элементов.

Тогда роль Y1 для второго элемента Б будет играть:

Параллельное соединение элементов не меняет функции, поэтому, с точки зрения логики, этот тип соединения не используется. Физически иногда все же применяют параллельное соединение элементов, но в основном для того, чтобы, например, усилить сигнал. В связи с этим, параллельное соединение элементов в алгебре логики не рассматривается.
Функция, которую выполняет элемент, вообще говоря, зависит от переменных, которые подаются на вход.
Поэтому перестановка аргументов влияет на характер функции.

Таким образом, произвольные, сколь угодно сложные в логическом отношении схемы, можно строить, используя два приема:
1. последовательное соединение элементов;
2. перестановка входов элементов.
Этим двум физическим приемам в алгебре логики соответствуют:
1. принцип суперпозиции (подстановка в функцию вместо ее аргументов других
функций);
2. подстановка аргументов (изменение порядка записи аргументов функций или замена одних аргументов функции другими).
Итак, физическая задача построения и анализа работы сложного устройства заменяется математической задачей синтеза и анализа соответствующих функций алгебры логики.
Элементарные функции алгебры логики
Существует несколько синонимов по отношению к функциям алгебры логики:
1. функции алгебры логики (ФАЛ);
2. переключательные функции;
3. булевские функции;
4. двоичные функции.
По мере необходимости будем пользоваться всеми этими синонимами.
Рассмотрим некоторый набор аргументов:

и будем считать, что каждый из аргументов принимает только одно из двух возможных значений, независимо от других
Чему равно число различных наборов?
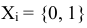
Поставим каждому набору в соответствие некоторое двоичное число:

Очевидно, что количество 
n-разрядных чисел в позиционной двоичной системе есть 
Допустим, что некоторая функция F(X1,X2,....Xn) задана на этих наборах и на каждом из них она принимает либо '0'-ое, либо '1'-ое значение.
Такую функцию называют функцией алгебры логики или переключательной функцией.
Чему равно число различных переключательных функций 'n' аргументов?
Т.к. функция на каждом наборе может принять значение '0' или '1', а всего различных наборов  , то общее число различных функций 'n' аргументов есть: 2*
, то общее число различных функций 'n' аргументов есть: 2*  .
.
По сравнению с аналитической функцией непрерывного аргумента даже для одного аргумента существует множество различных функций.
 9
9
Различные устройства ЭВМ содержат десятки и сотни переменных (аргументов), поэтому понятно, что число различных устройств, отличающихся друг от друга, практически бесконечно. Итак, нужно научиться строить эти сложные функции (а стало быть, и устройства), а также анализировать их.
Задача синтеза более сложных функций заключается в представлении их через простые на основе операций суперпозиции и подстановки аргументов.
Таким образом, вначале необходимо изучить эти элементарные функции, чтобы на их основе строить более сложные.
ФАЛ одного аргумента
Чтобы задать ФАЛ, нужно задать ее значения на всех наборах аргументов.

Будем у функции ставить индекс, эквивалентный набору ее значений для соответствующих значений аргумента, начиная с 0,0,....,0,..... и т.д. в порядке возрастания.
Эти функции можно реализовать на 4+х элементах, каждый из которых имеет максимум один вход. Таким образом, принципом подстановки аргументов для построения более сложных функций нельзя воспользоваться.
Необходимо рассмотреть более сложные функции, т.е. ФАЛ 2х аргументов.
Дадим такие определения:
1. ФАЛ, принимающие одинаковые значения на всех наборах аргументов,
называются равными.
2. ФАЛ существенно зависит от аргумента Хi, если

В противном случае она зависит не существенно, а соответствующий аргумент наз. фиктивным.
Например:


Видно, что Х3 – фиктивный аргумент. Это показывает, что в функцию можно ввести любое число фиктивных аргументов, от которых она существенно не зависит. Этот прием в дальнейшем потребуется для выполнения ряда преобразований.
Все ФАЛ от 2+х аргументов. Сведем их в единую таблицу

Эти функции введены формально. Однако им можно придавать определенный "логический" смысл. Алгебра логики часто называется исчислением высказываний.
При этом под высказываниями понимается всякое предложение, относительно которого можно утверждать, что оно истинно или ложно.
Например: В=<один плюс один + два> есть истинное высказывание.
Рассмотрим, какое смысловое содержание можно вложить в некоторые сложные высказывания на примере ФАЛ 2+х аргументов.
Инверсия
Читается НЕ Х или Х с чертой, отрицание Х.
Возьмем, например, такое высказывание: А=<Киев+столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т.е. не верно, что <Киев+столица
Франции>.
Из простых высказываний можно строить более сложные, применяя так называемые связи.
Логические связи – это ФАЛ, аргументами которых являются простые высказывания.
Конъюнкция
Возьмем 2 высказывания:
А=<Москва – столица РФ>
В=<дважды два + четыре>
тогда сложное высказывание: А &В будет истинным, так как истинны оба этих высказывания.
Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если истинному высказыванию приписать значение '1', а ложному + '0', то сложное высказывание можно назвать произведением.

Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания.

Дизъюнкция
Это сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.

Читается X1 ИЛИ X2: Некоторое отличие от смысла союза "или", принятого в русском языке: в данном случае этот союз употребляется в смысле объединения, а не разъединения.
