Экспоненциальный (показательный) закон распределения
Этот вид распределения находит широкое применение при решении практических вопросов надежности. Экспоненциальному закону распределения обычно подчиняются наработка на отказ ремонтируемых и неремонтируемых элементов при рассмотрении внезапных отказов, а также время безотказной работы сложных систем, прошедших период приработки и состоящих из элементов с различной интенсивностью отказов.
При экспоненциальном законе распределения имеют место следующие зависимости между основными количественными характеристиками надежности.
1. Плотность вероятности (дифференциальная функция) времени между отказами имеет вид
,
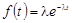где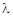 
- интенсивность отказов (параметр распределения); 
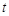- время безотказной работы (случайная величина); 
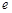- основание натурального логарифма, равное 2.7183.
2. Вероятность безотказной работы
.
3. Вероятность отказа
.
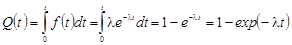4. Интенсивность отказов
.
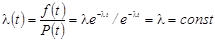Независимость интенсивности отказов от времени работы системы составляет главную отличительную особенность экспоненциального закона распределения случайной величины.
5. Среднее время безотказной работы
.
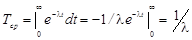6. Дисперсия
.
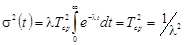7. Среднее квадратическое отклонение
,
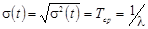т.е. среднее квадратическое отклонение равно среднему времени безотказной работы.
На практике это свойство часто используют для проверки истинности гипотеза о существовании экспоненциального закона распределения. Для этого на основе статистических данных определяют среднее квадратическое отклонение. Их равенство может служить доказательством правдоподобия принятой гипотезы.
Графическое изображение основных зависимостей при экспоненциальном запасе распределения показано на рис.1.
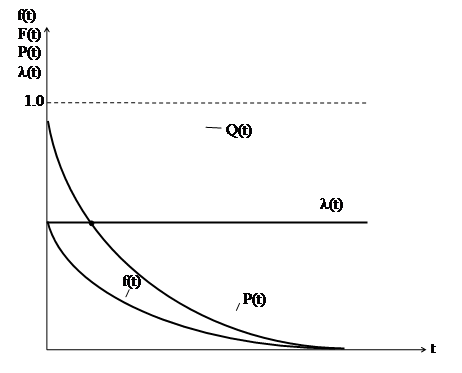
Рис. 1. Зависимости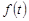 
, 
, 
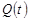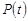и 
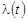
для экспоненциального закона распределения.
Нормальный закон распределения (закон Гаусса)
Нормальному закону распределения подчиняются только непрерывные случайные величины.
Плотность распределения
,
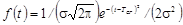Интегральная функция распределения
,
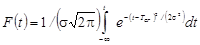где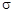 
- среднее квадратическое отключение;
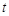- время безотказной работы;
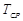- среднее значение (математическое ожидание) времени безотказной работы.
Нормальное распределение является двухпараметрическим и определяется параметрам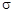и и 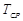. Этот закон описывает распределение случайной величины, значения которой группируются около среднего значения и наблюдаются с определенной частотой.
Пр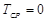и 
и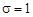 
получается центрированное и нормированное распределение. Дифференциальная 
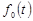и интегральная 
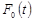функции этого распределения табулированы и имеют вид:
,
.
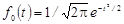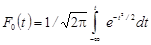При этом соблюдаются следующие равенства:
; 
;
.
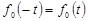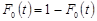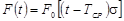Вероятность безотказной работы при нормальном законе распределения определяются по формуле
.
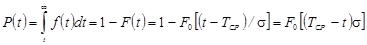Интенсивность отказов
.
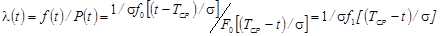Случайная величина, подчиняющаяся нормальному закону распределения, имеет следующие свойства:
- одинаковые положительные и отрицательные отклонения от средней арифметической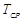 
равновозможны;
- меньшие отклонения более вероятны, чем большие;
- весьма большие отклонения от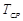 
маловероятны.
Вероятность того, что случайная величина, подчиняющаяся нормальному закону распределения, в процессе испытания примет значение, находящееся в пределах от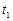 
до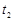 
может быть определена по формуле
,
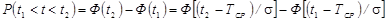где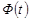 
- нормированная функция Лапласа. Для нормального закона распределения вероятность значений 
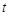, заключенных в пределах от 
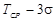до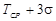 
составляет 0,9977, т.е. близка к единице.
Графическое изображение основных зависимостей при нормальном законе распределения показано на рис. 2.
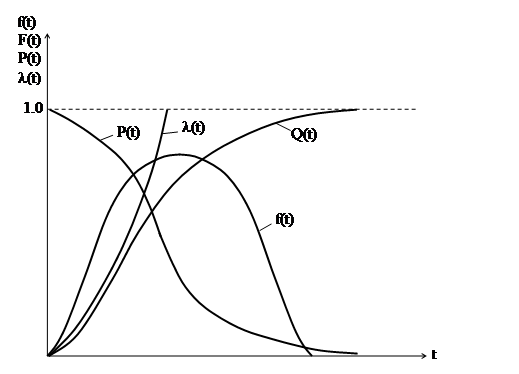
Рис. 2. Зависимост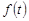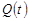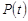и 
, 
, 
и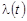 
для нормального закона распределения.
Закон распределения Вейбулла-Гнеденко
Распределение Вейбулла-Гнеденко используют при определении уровня надежности элементов в период приработки и установления наработки на отказ неремонтируемых изделий. Это распределение двухпараметрическое. Его параметрами являются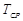 
и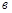 
- положительные постоянные.
Дифференциальная функция (плотность вероятности) распределения имеет вид
.
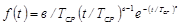Интегральная функция распределения Вейбулла-Гнеденко
.
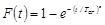