Лабораторная работа №13
МАЯТНИК ОБЕРБЕКА
Цель работы – экспериментальное изучение законов динамики вращательного движения твердого тела, а также зависимости момента инерции твердого тела от распределения массы относительно неподвижной оси вращения.
Приборы и принадлежности
Крутильный маятник Обербека, линейка, перегрузки с известной массой, секундомер.
Описание лабораторной установки
Маятник Обербека, применяемый в установке, представляет собой инерционное колесо в виде крестовины. На четырех взаимно перпендикулярных стержнях могут перемещаться четыре подвижных груза массой m1 каждый. На горизонтальной оси крестовины имеется двухступенчатый диск, на который наматывается нить. Один конец нити прикреплен к диску, а на втором конце нити подвешено несколько грузов массой m2 каждый. Под влиянием падающего груза нить разматывается с диска и вызывает вращательное равномерно ускоренное движение крестовины.
Общий вид маятника Обербека показан на рис. 1а. и 1б. На вертикальной колонне /1/, установленной на основании /2/, прикреплены два кронштейна: нижний неподвижный /3/ и верхний подвижный /4/ и две неподвижные втулки: нижняя /5/ и верхняя /6/. Основание /2/ снабжено регулируемыми ножками /7/, обеспечивающими горизонтальную установку прибора.
На верхней втулке /6/ посредством основания /8/ закреплен подшипниковый узел диска /9/. И диск /10/. Через диск /10/ перекинута нить /11/. Один конец нити прикреплен к двухступенчатому диску /12/, а на втором конце закреплены грузы /13/.
На нижней втулке /5/ посредством основания /14/ прикреплен тормозной электромагнит /15/, который после включения напряжения питания удерживает с помощью фрикционной муфты систему крестовины вместе с грузами в состоянии покоя.
Подвижный кронштейн /4/ можно перемещать вдоль колонны /1/ и фиксировать его в любом положении, определяя таким образом длину пути падения грузов. С целью определения этой длины на колонне /1/ нанесена миллиметровая шкала /16/.
На подвижном кронштейне /4/ закреплен фотоэлектрический датчик /17/. На неподвижном кронштейне /3/ закреплен фотоэлектрический датчик /18/, фиксирующий конец времени измерения и включающий тормозной электромагнит. К кронштейну /3/ прикреплен кронштейн /19/ с резиновыми амортизаторами, ограничивающими движение грузов.
 | |||
 | |||
В основании прибора имеется жестко скрепленный с ним миллисекундомер. Лицевая панель миллисекундомера показана на рис.1б. Клавиша W1 при нажатии включает (или выключает) напряжение сети. Клавиша W2 – сброс – устанавливает миллисекундомер на нулевое деление. Клавиша W3 – пуск – отключает тормозной электромагнит и вызывает движение грузов с одновременным началом счета времени движения. Значение времени дается в миллисекундах.

2. Краткая теория.
Вращательным движением твердого тела называется движение, при котором все точки тела, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, перпендикулярной к плоскости этих окружностей и называемой осью вращения.
Кратчайшее расстояние r от оси вращения до линии действия силы F, лежащей в плоскости, перпендикулярной оси вращения, и вызывающей вращение тела, называется плечом силы.
Момент силы M относительно той же оси (или вращательным моментом силы) называется произведение этой силы на плечо:

Единица момента силы в СИ – Н×м (ньютон×метр).
Момент силы считается положительным, относительно оси OZ, если поворот тела под действием силы происходит против хода часовой стрелки при наблюдении со стороны положительного конца оси OZ.
Если момент силы отличен от нуля, то тело вращается с угловым ускорением e. Угловое ускорение e - это величина, характеризующая быстроту изменения угловой скорости тела и равная первой производной угловой скорости по времени:
 .
.
Для бесконечно малого элемента массы тела dmi (т.е. для материальной точки массой dmi) момент силы dMi определится:

здесь аi и ui – ускорение и скорость элемента массы dmi. Так как величина:

(ri - плечо силы dFi), то получаем: 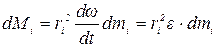
Суммируя по всем элементам массы тела, находим:
 (1)
(1)
где обозначено:

Величина, равная произведению массы материальной точки dmi на квадрат ее расстояния ri до оси вращения (то есть плеча), называется моментом инерции:

материальной точки относительно данной оси вращения. Сумма моментов инерции всех материальных точек твердого тела относительно оси вращения:
называется моментом инерции тела относительно данной оси. Единица момента инерции: [J]=кг×м2.
Уравнение (1) называется основным законом динамики вращательного движения и формулируется следующим образом: момент внешних сил, вращающий тело вокруг неподвижной оси, равен произведению момента инерции тела относительно этой оси на угловое ускорение тела.
При изменении расстояния перемещаемых грузов от оси крестовины данной лабораторной установки угловое ускорение e крестовины тем меньше, чем больше момент инерции тела J относительно оси вращения; из (1) имеем:
 .
.
Величина e может быть связана с ускорением падающего груза а формулой:
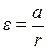 (3)
(3)
где r – радиус диска.
При равномерно ускоренном движении величину а можно связать с высотой падения грузов h и временем их падения t:
 (4)
(4)
Вращательный момент силы М, приложенный к крестовине, равен:
 (5)
(5)
здесь F – сила, воздействующая на диск; m – масса падающего груза, g – ускорение свободного падения. Величина:
 ,
,
где N – число грузов, m2 – масса каждого из них.
Подставляя (5) в (1) и используя (3) и (4), находим экспериментальное значение момента инерции:
 (6)
(6)
Теоретическое значение момента инерции JTеор:
 (7)
(7)
здесь Jo - суммарный момент инерции маховика без грузов, величина Jа – представляет собой момент инерции подвижного груза относительно оси, проходящей через его центр масс и параллельной оси вращения крестовины; l – расстояние от оси вращения до центра масс груза, m1 – масса каждого подвижного груза.
Величина:

в (7) есть не что иное, как момент инерции подвижного груза относительно оси вращения крестовины. При этом использована теорема Штейнера: момент инерции тела относительно оси вращения равен моменту инерции тела относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.
Если произвести измерения для двух значений l, скажем, для большего значения l1 и небольшого значения l2, то теоретическое значение разности моментов инерции согласно (7):
 . (8)
. (8)
Цель работы заключается в сравнении (8) с экспериментальным значением: DJэ=J1 - J2, определяемым по формуле (6) для двух времен падения груза соответственно: t = t1 и t = t2. При этом исключаются неизвестные величины Jo и Ja в формуле (7), которые не меняются при перемещении подвижных грузов по крестовине.
Конечно, приведенные рассуждения предполагают, что все четыре подвижных груза всякий раз находятся на одинаковых расстояниях l1 или l2 от оси крестовины. Эти расстояния, напомним, должны отсчитываться от центра масс (фактически от середины) подвижного груза, а не от его переднего или заднего края.