Пример реализации алгоритма в Excel

Лабораторная работа N 14. Численное интегрирование. Квадратурные формулы.

Задание

 

Вычислить интеграл 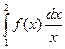с точностью e

· По формуле левых(правых) прямоугольников e=10^-1

· По формуле средних прямоугольников e=10^-2

· По формуле трапеций e=10^-2

· По формуле Симпсона e=10^-4

 

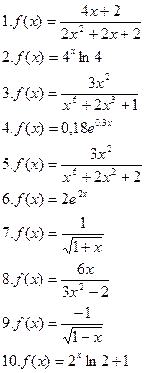
Алгоритмы применения формулы левых (правых) прямоугольников

1. Разбить отрезок [a,b] на n частичных отрезков (построить на отрезке [a,b] сетку с шагом h=(b-a)/n) x₀=a, x_i= x₀+i*h, i =1,2….n, x_n=b).

2. Вычислить значения функции f(x) в узлах сетки f_i= f(x_i).

3. Вычислить площади частичных прямоугольников по формуле левых прямоугольников

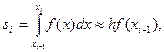
4.

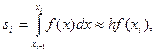или правых прямоугольников

 

5. Найти приближенное значение интеграла по формуле

6.

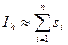Разбить отрезок [a,b] на 2n частичных отрезков (построить на отрезке [a,b] сетку с шагом h/2 x₀=a, x_i= x₀+i*h, i =1,2….n, x_n=b). Найти приближенное значение интеграла с новым шагом I_h/2.

7. Произвести оценку погрешности по формуле Рунге (p - порядок точности квадратурной формулы, для формулы левых и правых прямоугольников p=1)

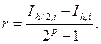
8. Продолжать уменьшать шаг, пока погрешность не станет меньше требуемой точности r_i<e.

9. Для проверки вычислить точное значение интеграла по формуле Ньютона-Лейбница.

 

Пример реализации алгоритма в Excel

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V
	Вычисление определенного интеграла по формуле левых прямоугольников (подинтегральная функция f(x)=1/x)
	Границы интегрирования
	A			n		количество частичных отрезков
	B			h	0,1	шаг сетки
	II
	Xi		1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
	Fi	1,00	0,91	0,83	0,77	0,71	0,67	0,63	0,59	0,56	0,53	0,50
	Si	0,1	0,09	0,08	0,08	0,07	0,07	0,06	0,06	0,06	0,05
	S h	0,71877140	Приближенное значение интеграла
	I	0,69314718	Точное значение интеграла
	Границы интегрирования
	A			n		количество частичных отрезков
	B			h	0,05	шаг сетки
	II
	Xi		1,05	1,1	1,15	1,2	1,25	1,3	1,35	1,4	1,45	1,5	1,55	1,6	1,65	1,7	1,75	1,8	1,85	1,9	1,95
	Fi	1,00	0,95	0,91	0,87	0,83	0,80	0,77	0,74	0,71	0,69	0,67	0,65	0,63	0,61	0,59	0,57	0,56	0,54	0,53	0,51	0,50
	si	0,05	0,05	0,05	0,04	0,04	0,04	0,04	0,04	0,04	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,03
	S h/2	0,705803382		приближенное значение интеграла
	I	0,693147181		точное значение интеграла
	r	0,01296802	погрешность

 

 

Алгоритм применения формулы средних прямоугольников

1. Разбить отрезок [a,b] на n частичных отрезков (построить на отрезке [a,b] сетку с шагом h=(b-a)/n) x₀=a, x_i= x₀+i*h, i =1,2….n, x_n=b).

2. Посчитать координаты средних точек частичных отрезков x_i-1/2= (x_i-1+ x_i)/2,

3. Вычислить значения функции f(x) в средних точках f_i-1/2= f(x_i-1/2).

4. Вычислить площади частичных прямоугольников по формуле средних прямоугольников

 

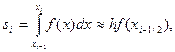
5. Найти приближенное значение интеграла по формуле

6.

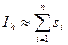Разбить отрезок [a,b] на 2n частичных отрезков (построить на отрезке [a,b] сетку с шагом h/2 x₀=a, x_i= x₀+i*h, i =1,2….n, x_n=b). Найти приближенное значение интеграла с новым шагом I_h/2.

7. Произвести оценку погрешности по формуле Рунге (p - порядок точности квадратурной формулы, для формулы средних прямоугольников p=2)

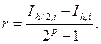
8. Продолжать уменьшать шаг, пока погрешность не станет меньше требуемой точности r_i<e.

9. Для проверки вычислить точное значение интеграла по формуле Ньютона-Лейбница.

 

Пример реализации алгоритма в Excel

 

 

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V
	Вычисление определенного интеграла по формуле средних прямоугольников (подинтегральная функция f(x)=1/x)
	Границы интегрирования
	A			n		количество частичных отрезков
	B			h	0,1	шаг сетки
	iI
	Xi		1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
	Xi-1/2	1,05	1,15	1,25	1,35	1,45	1,55	1,65	1,75	1,85	1,95
	Fi	1,00	0,91	0,83	0,77	0,71	0,67	0,63	0,59	0,56	0,53	0,50
	Fi-1/2	0,95	0,87	0,80	0,74	0,69	0,65	0,61	0,57	0,54	0,51
	si	0,09	0,08	0,08	0,07	0,06	0,06	0,06	0,05	0,05	0,05
	Sh	0,69283536	Приближенное значение интеграла
	I	0,69314718	Точное значение интеграла
	Границы интегрирования
	A			n		количество частичных отрезков
	B			h	0,05	шаг сетки
	II
	Xi		1,05	1,1	1,15	1,2	1,25	1,3	1,35	1,4	1,45	1,5	1,55	1,6	1,65	1,7	1,75	1,8	1,85	1,9	1,95
	Xi-1/2	1,03	1,08	1,13	1,18	1,23	1,28	1,33	1,38	1,43	1,48	1,53	1,58	1,63	1,68	1,73	1,78	1,83	1,88	1,93	1,98
	Fi	1,00	0,95	0,91	0,87	0,83	0,80	0,77	0,74	0,71	0,69	0,67	0,65	0,63	0,61	0,59	0,57	0,56	0,54	0,53	0,51	0,50
	Fi-1/2	0,98	0,93	0,89	0,85	0,82	0,78	0,75	0,73	0,70	0,68	0,66	0,63	0,62	0,60	0,58	0,56	0,55	0,53	0,52	0,51
	si	0,04	0,04	0,04	0,04	0,04	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,03	0,02	0,02	0,02	0,02	0,02	0,02
	Sh/2	0,693069098		приближенное значение интеграла
	I	0,693147181		точное значение интеграла
	r	7,79126E-05	погрешность