Теоретическая часть. Описание установки.

Лабораторная работа № 16

Температурный коэффициент давления.

Шкала Кельвина.

Цель работы: экспериментальное определение температурного коэффициента давления и температуры абсолютного нуля по шкале Цельсия.

Оборудование: установка, включающая вольтметр, пневмосистему (кран-зажим и два штуцера) к манометру, секундомер, мультиметр, калькулятор инженерный, чайник электрический, баллон металлический со штуцером и шлангом, термопара к мультиметру.

Продолжительность работы – 4 часа

Теоретическая часть. Описание установки.

 

Температура – одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Представление о температуре вошло в науку через посредство наших чувственных восприятий. Наши ощущения позволяют различать качественные градации нагретости: теплый, холодный, горячий и пр. Однако количественная мера степени нагретости, пригодная для науки, не может быть установлена с помощью чувственных восприятий. Ощущения субъективны. В зависимости от состояния руки одно и то же тело на ощупь может казаться либо теплым, либо холодным.

В основу количественного определения температуры и построения точной температурной шкалы должны быть положены объективные физические явления и факты, свободные от субъективизма чувственных восприятий. К понятию температуры можно подходить с различных точек зрения. Наиболее общим является понятие термодинамического равновесия.

Когда соприкасаются два тела (или несколько тел), между ними происходит теплообмен. Если система тел изолирована (т.е. не взаимодействует с окружающими телами и внешней средой), теплообмен будет длиться до тех пор, пока в системе не прекратятся всякие макроскопические изменения. Тогда говорят, что эти тела находятся в термодинамическом равновесии друг с другом и имеют одинаковые температуры. Таким образом, температура есть одна из макроскопических характеристик состояния термодинамического равновесия изолированной системы тел, хотя ей постоянно пользуются также в тех случаях, когда полного термодинамического равновесия еще нет.

Для того, чтобы количественно определить температуру, нужно найти такую величину, которая была бы одинаковой для любых тел, находящихся в состоянии теплового равновесия. Рассмотрим систему, состоящую из различных газов каждый из которых заключен в сосуд с теплопроводящей оболочкой и пусть эти газы находятся в тепловом равновесии. Экспериментальные исследования свойств газов показали, что отношение произведения давления газа P на его объем V к числу молекул N оказывается одинаковым:

. (1)

Этот опытный факт позволяет принять величину q в качестве естественной меры температуры (величину q принято называть газовой температурой). Молекулярно-кинетическая теория позволяет нам представить физическую сущность этого сложного понятия – температура. Используя основное уравнение молекулярно-кинетической теории

,

где - концентрация газа, - средняя кинетическая энергия поступательного движения молекулы, получим:

.

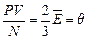Следовательно, средняя кинетическая энергия молекул любых газов, находящихся в тепловом равновесии, одинакова. Величина q равна двум третям средней кинетической энергии беспорядочного теплового движения молекулы газа и выражается в джоулях.

В физике обычно температуру выражают в градусах, принимая, что температура T в градусах и величина q связаны уравнением:

, (2)

где k – коэффициент пропорциональности, зависящий от выбора единицы температуры.

Учитывая (1) и (2) получаем:

. (3)

Практически измерение температуры на основании использования уравнения (3) осуществляется с помощью газового термометра (рис 1). Газовый термометр представляет собой сосуд постоянного объема, в котором находится газ, и манометр, служащий для измерения давления. Поскольку количество газа остается неизменным давление может служить мерой температуры газа, а значит, и любого тела, с которым газ находится в тепловом равновесии.

Шкала измерения температуры в соответствии с уравнением (3) носит название абсолютной шкалы температур или шкалы Кельвина по титулу английского физика Уильяма Томсона, ее предложившего (президент английского королевского общества У. Томсон в 1892 г. получил титул лорда Кельвина).

 

Рис.1 Газовый термометр. Рис.2 Соответствие шкалы Цельсия

и абсолютной шкалы температур.

 

До введения абсолютной шкалы температур в практике получила широкое распространение шкала измерения температуры по Цельсию. Единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия:

1⁰К = 1⁰C.

По шкале Цельсия (международной практической), основанной на двух реперных точках, температуры замерзания и кипения воды при давлении 1,013×10⁵ Па соответственно равны 0⁰ и 100⁰ C.

Шкала Кельвина (термодинамическая) определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии). Температура замерзания воды оказывается при этом равна 273,15К (при том же давлении, что и по шкале Цельсия). Поэтому, при любой температуре t по Цельсию значение абсолютной температуры T выше на 273.15 градуса (рис.2):

T=273.15+ t. (4)

Температура T=0 называется нулем Кельвина или абсолютным нулем, ему соответствует .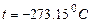

Выражение (1) с учетом (3) позволяет получить соотношение:

, (5)

где С - постоянная, зависящая только от массы и химической природы газа. Из этого выражения следует что, произведение объема V данной массы газа на его давление P зависит только от температуры. При Т = 0 это уравнение дает . На этом основании заключают, что при такой температуре , так как объем V в нуль обращаться не может. Это означает, что при абсолютном нуле атомно-молекулярное движение прекращается. В действительности это не так. При абсолютном нуле остается еще весьма интенсивное движение частиц, из которых состоит тело. Ему соответствует минимальная энергия, которая от тела уже не может быть отнята. Но это движение уже не является тепловым. Соответствующая ему энергия называется нулевой энергией.

Таким образом, абсолютный нуль может быть определен как такая температура, при которой в теле прекращается тепловое движение и остается только движение частиц, связанное с нулевой энергией.

Используя выражение (4), уравнение (5), можно записать в виде:

, (6)

где Р ₀ и V ₀ - давление и объем газа при температуре t = 0⁰ C, a - постоянный коэффициент, численное значение которого приближенно равно

К^-1.

Этому коэффициенту можно дать двоякое физическое толкование.

Во-первых, если давление газа поддерживать постоянным, то формула (6) переходит в

(7)

и показывает, что есть коэффициент теплового объемного расширения газа.

Во-вторых, если поддерживать постоянным объем газа, то формула (6) примет вид:

. (8)

Так как Р ₀ – давление газа при 0°С, то приращение давления при нагревании на 1°С есть . При нагревании газа на t градусов приращение давления бу­дет в t раз больше, т. е. приращение давления пропорцио­нально приращению температуры.

Величина a_p, показывающая, на какую часть давления при 0°С увеличивается давление газа при нагревании на 1°С, имеет одно и то же значение (точнее, почти одно и то же) для всех газов

 

(9)

называется температурным коэффициентом давления газа.

Для идеальных газов коэффициент объемного расширения и температурный коэффициент давления совпадают.

Экспериментальная часть

 

Упражнение 1. Подготовка установки к измерению.

Налейте в чайник, в котором находится металлический баллон со штуцером Ш и шлангом, холодную воду так, чтобы вода поднялась до крышки баллона (рис.3). Подсоедините термопару Т к установке. Для этого провода со штеккерами вставьте в два нижних гнезда, расположенных в правом углу мультиметра. Третий провод подсоедините к клемме, расположенной на задней панели установки. Свободный конец опустите в чайник. Подождите 2 ÷ 3 минуты и после этого подключите баллон к манометру (наденьте трубку на штуцер Ш1). Второй вход манометра заглушите – закройте кран К1. Убедитесь, что переключатель мультиметра находится в положении - . Измерьте термопарой температуру воды . Определите по настенному барометру атмосферное давление .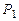

 

 

Рис.3 Схема установки, применяемая в данной работе.

 

Упражнение 2. Проведение измерений.

Включите чайник и нагрейте воду на 5 ÷ 6 . Выключите чайник. Подождите пока давление и температура перестанут меняться. Это занимает около 2 минут. Запишите показания манометра и мультиметра. Манометр показывает избыточное давление

D P=P₂-P₁,

где P₂ – новое давление в баллоне при температуре t₂.

Продолжайте снимать зависимость избыточного давления от температуры, пока температура в чайнике не достигнет 90⁰ C. До кипения воду не доводить!

Перед тем как приступить к расчетам, отключите термопару и уберите ее в ящик, расположенный на установке. Снимите шланг со штуцера Ш1 и вылейте горячую воду из чайника. После слива воды шланг на штуцер не одевать!

Постройте график зависимости избыточного давления D P от приращения температуры .При построении графика считайте, что погрешность манометра составляет , а погрешность термопары . Из уравнения (9), которое можно переписать в виде

, (10) следует, что эта зависимость должна быть линейной. Давление P ₀ газа в сосуде при t=0⁰C можно рассчитать из соотношения (8):

Р₀=Р₁ / (1+α_pt ₁) (11)

С учетом (11) выражение (10) преобразуем следующим образом:

∆ P=α_pP₁ ∆t / (1+α_pt ₁) (12)

Из углового коэффициента ν прямой (11) можно рассчитать экспериментальное значение температурного коэффициента давления α_p:

α_p=ν/ (P₁ –νt₁) (13)

Оцените погрешность величины α_p и сравните ее с теоретическим значением.

Подготовка к работе

 

1. Физические понятия:

Макроскопические и микроскопические параметры газовой системы;

Термодинамическое равновесие, температура;

Уравнение Менделеева-Клапейрона, изопроцессы;

Газовый термометр;

Способы измерения температуры;

Шкала измерения температур по Кельвину и Цельсию;

Основное уравнение МКТ;

Взаимосвязь температуры со средней энергией молекулы;

Понятие о степенях свободы молекул идеального газа;

Коэффициент объемного расширения газа;

Температурный коэффициент давления.

 

2. Приведите вывод основного уравнения молекулярно-кинетической теории идеального газа:

P=⅔n^.E

3. Покажите взаимосвязь уравнения (3) из описания лабораторной работы с уравнением состояния идеального газа в форме Менделеева-Клапейрона.

4. Расчетное задание:

Рассчитайте зависимости ΔР от Δt в соответствии с формулой (10) описания лабораторной работы для величин давлений Р₁ равных 740, 750, 760 мм.рт.ст. Температурный коэффициент давления α_р считайте равным 1/273,15 град ^-1, а температуру t₁ задайте равной 20⁰С.

 

5. Сформулируйте основную цель работы и порядок ее выполнения.

 

 

 

Примечание. Пункты 2,3.4 выполните письменно при подготовке конспекта

по лабораторной работе.

 

 

Литература

1. Савельев И.В. Курс общей физики-М.: Астрель ^. АСТ, 2005-Т.3 §§1.7, 1.8, 2.2-2.5,3.3.

2. Иродов И.Е. Общая физика, Физика макросистем- М.: Бином. Лаборатория знаний, 2004, §§1.1, 1.2, 1.4-1.6, 2.2.