Государственное бюджетное профессиональное образовательное учреждение
Ивановское художественное училище им. М.И. Малютина
РЕФЕРАТ
На тему:
«Разработка А.М. Ляпуновым общей теории устойчивости»
Выполнила: Шенягина Анастасия, гр. 1Г
Преподаватель:
Г. Иваново
Г.
Содержание
1. Введение 3
2. Краткая биография Ляпунова А.М. 4-5
3. Разработка теории устойчивости 6-17
4. Заключение 18
5. Список используемой литературы 19
ВВЕДЕНИЕ
На протяжении всей жизни Александр Михайлович Ляпунов работал в самых сложных областях механики и математики. Но наибольший интерес у него вызывали вопросы устойчивости сложных механических систем, находящихся в непрерывном движении. Самое главное достижение Ляпунова — создание теории устойчивости. Теория описывает многие происходящие в мире события, причем самых разных масштабов — от микроскопических до космических. Ученый много лет работал над проблемой устойчивости движения механических систем и достиг немалых успехов — в современных математике, физике, механике, астрономии и технике используются сформулированные им методы и приемы решения задач.
КРАТКАЯ БИОГРАФИЯ
Ляпунова А.М.
Александр Михайлович Ляпунов родился 25 мая (6 июня) 1857 года в Ярославле. Его отец, Михаил Васильевич, был известным астрономом. Начальное образование получил дома, после смерти отца (в 1868 году) обучался в семье дяди.
В 1870 году Александр с матерью и братьями переехал в Нижний Новгород, где поступил в гимназию, которую окончил с золотой медалью в 1876-м. После сразу же поступил на естественное отделение физико-математического факультета Санкт-Петербургского университета, однако уже через месяц перевелся на более интересное ему математическое отделение.
После окончания университета (в 1880 году) Ляпунов остался в его стенах для подготовки к профессорскому званию. В 1881-м вышли первые математические научные работы Ляпунова, а в 1882-м он начал работу над магистерской диссертацией. Тему задал его руководитель, знаменитый ученый Пафнутий Чебышев, однако она оказалась настолько сложной, что диссертацию Ляпунов написал лишь спустя 20 лет.
С 1885 года Ляпунов — приват-доцент, в этом же году переезжает из Санкт-Петербурга в Харьков, где занимается преподаванием, но не оставляет и науку. В 1892-м ученый защищает докторскую диссертацию под названием «Общая задача об устойчивости движения». Этому труду суждено было стать фундаментальным и основополагающим в теории устойчивости.
В 1900 году Александр Михайлович Ляпунов стал членом-корреспондентом Санкт-Петербургской академии наук. В 1902-м он возвращается в Санкт-Петербург и активно работает над различными аспектами теории устойчивости и другими научными проблемами.
В 1917 году из-за болезни жены Ляпунов с семьей переехал в Одессу. 31 октября 1918 года жена умерла, и вечером этого же дня ученый выстрелил себе в голову и в течение трех дней находился в бессознательном состоянии, а 3 ноября скончался в университетской хирургической клинике.
РАЗРАБОТКА ТЕОРИИ УСТОЙЧИВОСТИ
Основной работой A. М. Ляпунова (1857—1918) была теория устойчивости движения.
Первым этапом в решении задачи на равновесие было определение положения равновесия, или закона движения тела; стали решаться задачи на равновесие тел или механической системы. После определения положения равновесия, вставал вопрос: будет ли найденное положение соответствовать устойчивому или неустойчивому равновесию? Практическое значение могли иметь только устойчивые положения; они характеризовались тем, что находящиеся в таком положении тела, при небольшом отклонении, автоматически возвращались в положение равновесия. Может быть, впервые такая задача была поставлена в приписываемых Аристотелю «Механических проблемах».
Такой же задачей занимался и Архимед, рассматривавший положение равновесия тяжелого параболического сегмента, плававшего в жидкости различной плотности; как истинный практик Архимед рассматривал лишь устойчивые положения равновесия, проверяя, может ли рассматриваемое тело, будучи выведено из положения равновесия, самостоятельно в него вернуться.
После него во избежание затруднительной работы стремились получить критерий, при помощи которого можно было бы без расчетов определить, будет ли данное положение равновесия устойчивым или нет. Первый такой критерий для механической системы тел, находящихся под действием силы тяжести, дал ученик Галилея Торричелли (1608 — 1647); он указал, что устойчивое равновесие соответствует таким положениям системы, в которых высота центра тяжести имеет минимальное значение. Для часто встречающегося случая, когда тяжелое тело имеет только одну точку опоры, принцип Торричелли толковался так, что устойчивое положение равновесия получается, когда центр тяжести находится ниже точки опоры. 
Обобщение второго принципа для сил, обладающих силовой функцией, было дано теоремой Дирихле (1805—1859).
Случай устойчивости равновесия системы тел, имеющей несколько степеней свободы, был рассмотрен Лагранжем при помощи обычного в настоящее время приема — «первого приближения, когда дело сводилось к рассмотрению системы линейных дифференциальных уравнений; если для небольших отклонений получались уравнения, соответствующие гармоническим колебаниям, то положение равновесия считалось устойчивым. Для этого требовалось, чтобы корни характеристического уравнения, при помощи которого определяются возможные периоды колебаний, были мнимыми.
Вопрос об устойчивости движения возник в XVIII в. на чисто астрономической почве. После того как было установлено, что движения небесных тел не являются вечными «по своей природе», а совершаются под действием сил всемирного тяготения, необходимо было решить, можно ли считать эти движения устойчивыми. Имелось в виду только периодическое движение планет, совершающееся по эллипсам, близким к окружностям. Если рассматривать движение только под действием силы притяжения Солнца, то возможности падения планеты на Солнце или, наоборот, удаления от него устранялись при помощи законов площадей и сохранения энергии; при наличии трансверсальной скорости планета, приближаясь к Солнцу, увеличивала свою скорость и таким образом ускользала от него; при удалении же от Солнца ее скорость тормозилась работой силы притяжения к Солнцу и планета должна была возвращаться к нему.
Однако на планеты кроме Солнца действуют также силы притяжения и других планет. Если эти возмущения будут все время действовать в одном и том же направлении, то кроме возмущений, носящих характер колебательных движений и со временем не могущих превзойти некоторой предельной величины, могут возникнуть и вековые возмущения, способные произвести с течением времени очень заметное изменение в движении рассматриваемой планеты. Исследованием этих возмущений занялся Лаплас, показавший в своей «Небесной механике», что для Солнечной системы вековые возмущения незначительны и устойчивость движений всех планет можно считать обеспеченной на очень долгое время.
Планеты далеко не всегда можно рассматривать как материальные точки; в действительности они даже являются не сферами, а всего лишь сфероидами. Таким образом, встает вопрос об устойчивости движений тел конечных размеров. Впервые этот вопрос возник при исследовании движения твердого тела в случае Пуансо — Эйлера. Было показано, что без воздействия посторонних сил тела могут вращаться только вокруг осей, совпадающих с главными центральными осями инерции, причем устойчивыми будут вращения только вокруг осей, для которых момент инерции является или наибольшим, или наименьшим.
Развитие машинной техники в XIX в. поставило еще одну задачу — регулирование хода машин, а именно получение равномерной скорости (или близкой к равномерной), когда действующие силы являются переменными. Простейшим таким прибором является обыкновенный маховик, снимающий избыток кинетической энергии при ускоренном движении и вновь отдающий его при замедлении. Затем последовали и другие типы регуляторов, изучение которых стало предметом особой дисциплины — теории регулирования хода машин. В последнее время эти вопросы стали еще более актуальными в связи с проведением автоматизации в различных отраслях промышленности: наряду с обыкновенным возникло еще автоматическое регулирование хода машин, которое развивается особенно быстро в связи с успехами строительства и оборудования скоростных самолетов и спутников.
Вопрос об автоматизации управления ставит новые задачи перед механикой. С одной стороны, заданное движение можно поддерживать путем автоматических силовых воздействий — автоматическое регулирование; с другой стороны, можно сохранить имеющееся движение при помехах и возмущениях со стороны внешних факторов, не зависящих от воли человека. Определением прочности или устойчивости движения против случайных возмущений, имеющих небольшую величину, занимались Раус (Routh), Н. Е. Жуковский, Анри Пуанкаре, но наибольшие успехи сделал А. М. Ляпунов.
В своих работах Ляпунов взялся за решение труднейшей задачи: определение устойчивости в общем случае нелинейной, нестационарной, взаимосвязанной системы любого порядка. Первоначально вспомогательный, вопрос о критериях устойчивости формы вращающегося жидкого тела постепенно перерос в гениальную общую теорию устойчивости движения, не превзойденную до сих пор.
При этом Ляпунов использовал работы по качественному анализу дифференциальных уравнений Пуанкаре, с которым состоял в постоянной переписке. Однако, в отличие от последнего, русский математик признавал только строгие аналитические методы доказательства, а в решениях с помощью рядов давал полную оценку сходимости, никогда не ограничиваясь первым приближением. Это делало его работы весьма трудными для понимания, что неоднократно отмечалось его современниками, последователями и студентами. Мнение одного известного французского математика, который ответил на присланную докторскую диссертацию Ляпунова словами: «Наверное, это прекрасная работа; к сожалению, моей жизни не хватит для того, чтобы понять ее».
Основные заслуги Ляпунова в решении проблемы устойчивости состоят в следующем.
Прежде всего, он дал точное математическое определение понятию устойчивости. Не прибегая к математическим обозначениям, ограничимся понятием асимптотической устойчивости, имеющим наибольшее практическое значение. Предположим, что система находится в некотором положении равновесия. Тогда она асимптотически устойчива, если после ее принудительного выведения из этого исходного положения она самостоятельно в него возвращается.
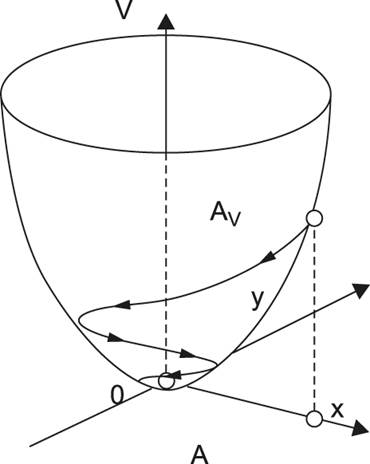
Рис. 1. Пример функции Ляпунова
Наиболее важным является так называемый «прямой метод Ляпунова», который определяет условия устойчивости системы самого общего вида. К примеру, рассмотренная выше система в двухмерном пространстве состояния асимптотически устойчива по Ляпунову, если существует некоторая положительно определенная функция V (x, y, t), полная производная по времени которой, найденная в соответствии с уравнениями состояния системы, отрицательна для всех t? t 0. Такая функция V называется сейчас функцией Ляпунова.
Смысл этого условия для нашего примера виден на рис. 1, где функция Ляпунова показана в виде параболоида V.
Если в начале движения при t = t 0 изображающей точке А соответствует точка А V на поверхности этого параболоида, то с течением времени значение функции V стремится к началу координат, поскольку в любой точке все ее производные по времени убывают. Для этого примера механической системы второго порядка физический смысл функции Ляпунова очень простой — это полная энергия системы в виде суммы ее кинетической и потенциальной энергий. Очевидно, что если в процессе движения она постоянно убывает (производная отрицательная) в данном случае за счет трения, то тело, в конце концов, придет в состояние равновесия.
Для более сложной системы, имеющей N переменных состояния x 1, x 2,… xN, функция Ляпунова V (x 1, x 2,… xN, t) может иметь совсем другой физический смысл, но формулировка условия устойчивости будет аналогична вышеприведенной.
Ляпунов разрешил труднейшую проблему устойчивости в самом общем виде. О справедливости его методов свидетельствовал многолетний спор с Пуанкаре и другим известным математиком и астрономом, сыном знаменитого Чарльза Дарвина и президентом английского астрономического общества — Джорджем Дарвином (George Darwin). Последний выдвинул космогоническую гипотезу о процессе образования Луны, который, по его мнению, протекал следующим образом. Одна из жидких планет Солнечной системы, называемая Протоземля, имеющая эллипсоидальную форму, вследствие быстрого вращения приняла за счет центробежных сил сначала сигарообразную, а затем и грушевидную форму, названную так по предложению Пуанкаре. Со временем за счет все тех же центробежных сил маленькая головка этой «груши» отделилась, образовав спутник материнской планеты — Луну. Процесс этот протекал миллионы лет, и ученые понимали, что для его реализации необходимо, чтобы все промежуточные формы этой Протоземли были устойчивыми. Вопрос, таким образом, упирался в проблему устойчивости форм вращающейся жидкости.
Пуанкаре в свойственной ему интуитивной манере решил эту задачу, ограничившись первым приближением, которое указывало на устойчивость грушевидной формы. Но он понимал недостаточность такого подхода, поэтому, когда Дарвин обратился к нему с этим вопросом, Пуанкаре посоветовал ему просчитать второе приближение, снабдив формулами и методикой расчета. Взявшись за этот труднейший расчет, Дарвин в конце концов довел его до успешного решения и с удовлетворением обнаружил, что и во втором приближении грушевидная форма может быть устойчивой. Это было воспринято научным сообществом как несомненное доказательство гипотезы Дарвина.
Однако с этим не согласился Ляпунов. В своей магистерской диссертации он писал о возможности грушевидной формы вращающейся жидкости, но не мог проверить ее устойчивость. Спустя двадцать лет он вернулся к этому вопросу, вооруженный своей общей теорией устойчивости, и нашел точное решение задачи, показывающее неустойчивость грушевидной формы. Он указал и на источник неверных заключений Пуанкаре и Дарвина, заключавшийся в использовании только первых двух членов разложения ряда.
Тем не менее, западное научное сообщество поддерживало гипотезу Дарвина. В 1912 г. скончались два участника спора — Пуанкаре и Дарвин, и вопрос оставался подвешенным до 1917 г., когда известный английский математик и астроном Джеймс Джинс (James Jeans) опубликовал свои расчеты по третьему приближению злополучной задачи. На этот раз грушевидная форма оказалась неустойчивой, что несомненно доказало правоту Ляпунова.
Впоследствии гипотеза Дарвина была опровергнута и геохимическими исследованиями лунных пород, и после экспедиции американцев на Луну преобладающей стала теория удара, согласно которой Протоземля столкнулась с другой, меньшей планетой Солнечной системы, вызвав выброс вещества земной мантии, принявшего затем шарообразную форму нашей спутницы.
Однако современники не смогли оценить глубину и перспективность идей Ляпунова, и долгое время его работы не замечались западным научным сообществом, хотя Александр Михайлович публиковал большинство своих работ на французском языке и состоял в постоянной переписке с ведущими европейскими математиками. Его знаменитая диссертация была полностью переведена на французский язык в 1907 г., а на английский — только через сто лет после ее защиты, в 1992 г.
Идеи Пуанкаре и Ляпунова развивались преимущественно в Советском Союзе, рядом известных школ автоматического управления: горьковской (А. А. Андронов), казанской (Н. Г. Четаев, И. Г. Малкин), киевской (Н. М. Крылов, Н. Н. Боголюбов), московской (Б. В. Булгаков), ленинградской (А. И. Лурье, В. И. Зубов, В. А. Якубович) и др.
Но только после запуска в 1957 г. в Советском Союзе первого спутника Земли, когда выяснилось, что синтез алгоритмов управления ракетно-космическими системами может эффективно выполняться с использованием метода функций Ляпунова, западные ученые стали внимательно изучать и развивать его труды. Во второй половине XX века методом Ляпунова была доказана справедливость классических критериев устойчивости Рауса-Гурвица и Найквиста [8]. Сегодня термины «метод функций Ляпунова», «определения устойчивости Ляпунова», «устойчивость по Ляпунову» являются общепризнанными и используются в научных публикациях, независимо от языка их написания.
Потребность в создании теории устойчивости впервые возникла в небесной механике для решения двух важных задач: устойчивости взаимного движения планет и происхождения их видимой формы.
Первая задача начиналась с определения устойчивости движения трех тел, а вторая упиралась в устойчивость особой грушевидной формы вращающейся жидкой массы планеты до ее затвердевания. Основополагающий вклад в этом направлении внесли работы французского ученого Пуанкаре и российского математика Ляпунова.
Пуанкаре, опираясь на созданный им качественный анализ дифференциальных уравнений, установил, что движение трех тел может быть хаотическим и лишь в частных случаях устойчивым периодическим.
Задача о форме вращающейся жидкости стала особенно острой после создания английским астрономом Дарвином гипотезы образования Луны вследствие отделения части планеты Протоземля, имевшей грушевидную форму, устойчивость которой подтвердил в первом приближении Пуанкаре, а во втором — сам Дарвин.
Однако с этим не согласился Ляпунов, который, создав общую теорию устойчивости систем, нашел общее решение задачи, несомненно, показывающее неустойчивость грушевидной формы и, следовательно, несостоятельность гипотезы Дарвина.
Теория устойчивости движения занимается исследованием влияния возмущающих факторов на движение материальной системы. Под возмущающими факторами понимаются силы, не учитываемые при описании движения вследствие их малости по сравнению c основными силами. Эти возмущающие силы обычно неизвестны. Они могут действовать мгновенно, что сведется к малому изменению начального состояния материальной системы, т. е. начальных значений координат и скоростей. Но эти факторы могут действовать и непрерывно, что будет означать, что составленные дифференциальные уравнения движения отличаются от истинных, что в них не учтены некоторые малые поправочные члены.
Хорошо известно, что влияние малых возмущающих факторов на движение материальной системы будет неодинаковым для различных движений. На одни движения это влияние незначительно, так что возмущенное движение мало отличается от невозмущенного. Напротив, на других движениях влияние возмущений сказывается весьма значительно, так что возмущенное движение значительно отличается от невозмущенного, как бы малы ни были возмущающие силы. Движения первого рода называются устойчивыми, движения второго рода — неустойчивыми.
Теория устойчивости движения и занимается установлением признаков, позволяющих судить, будет ли рассматриваемое движение устойчивым или неустойчивым.
Так как в действительности возмущающие факторы всегда неизбежно существуют, то становится понятным, что задача устойчивости движения приобретает очень важное теоретическое и практическое значение.
Задачей устойчивости движения занимались многие виднейшие математики и механики. Основная теорема об устойчивости равновесия установлена еще Лагранжем. Она служила исходным пунктом для исследований Рауса, который установил признаки устойчивости движения для некоторых частных случаев движений. Задачей устойчивости занимались также Томсон и Тэт и Н. Е. Жуковский. Все эти авторы рассматривали весьма частные случаи движений и для решения задачи применяли нестрогие методы. Первое строгое решение задачи принадлежит Пуанкаре. Однако результаты Пуанкаре также носят весьма частный характер.
В 1892 году появилась знаменитая докторская диссертация А. М. Ляпунова «Общая задача об устойчивости движения». В этом замечательном труде задача об устойчивости движения была впервые поставлена во всей ее общности и были предложены мощные и вместе с тем строгие методы ее решения. Эта работа Ляпунова явилась отправным пунктом всех дальнейших исследований по теории устойчивости движения.
Выше было дано весьма схематичное определение устойчивости и неустойчивости движения. Эти понятия требуют, разумеется, более точного определения. Различные авторы по-разному определяли эти понятия и вследствие этого по-разному ставили задачу устойчивости. Наиболее общая постановка задачи дана Ляпуновым. Эта постановка оказалась исключительно удачной и наиболее соответствующей нуждам приложений. Этим и объясняется тот особый интерес, который проявлен к теории Ляпунова в последние годы, когда современная техника, в которой приходится иметь дело с огромными скоростями и широким внедрением автоматики, сделала особо актуальной задачу об устойчивости движения.
ЗАКЛЮЧЕНИЕ
Теория устойчивости находит самое широкое применение во многих областях науки и техники. С ее помощью можно рассчитать, как будет вести себя любая находящаяся в движении механическая система любого масштаба. Например, она даст ответы на вопросы, как продолжится полет ракеты при резких порывах ветра или иных воздействиях, как будет двигаться автомобиль после столкновения с другим автомобилем или наезда на камень, как продолжится вращение небесных тел вокруг общего центра масс при возмущениях, оказываемых сторонним объектом, и тому подобные.
Литература
1. Борислав Славолюбов. История открытия Нептуна.
2. Микеров А. Г. Классики линейной теории автоматического регулирования. Control Engineering – Россия. 2015. № 1 (55).
3. Тяпкин А. А. Шибанов. А. С. Пуанкаре. М.: Молодая гвардия. 1982.
4. Ball R., Holmes P. Dynamical systems, stability and chaos.
5. Шибанов А. С. Александр Михайлович Ляпунов. М.: Молодая гвардия. 1985.
6. Цыкало А. Л. Александр Михайлович Ляпунов. 1857 — 1918. М.: Наука. 1988.
7. Петров Ю. П. Очерки истории теории управления. СПб.: БХВ — Петербург. 2012.
8. Bernstein D. S. From Infancy to Potency: 1857 — 1918. Lyapunov’s second method and the past, present and future of control theory.
9. Галимов Э. М. Происхождение Луны. Российская концепция против «американской». Земля и Вселенная. 2005. №6.
10. https://www.proza.ru
11. https://math4school.ru