гуляева татьяна ивановна, доктор экон. наук, профессор
Ректор ФГБОУ ВО «Орловский государственный аграрный университет им. Н.В. Парахина», г. Орел
Тел., е-mail:
коломейченко Алла сергеевна, кандидат экон. наук, доцент
Зав. кафедрой ФГБОУ ВО «Орловский государственный аграрный университет им. Н.В. Парахина», г. Орел
Тел., е-mail:
польшакова наталья викторовна, кандидат экон. наук, доцент
Доцент ФГБОУ ВО «Орловский государственный аграрный университет им. Н.В. Парахина», г. Орел
Тел., е-mail:
Шуметов вадим георгиевич, доктор экон. наук, профессор
Профессор ФГБОУ ВО «Орловский государственный аграрный университет им. Н.В. Парахина», г. Орел
Тел. 910-300-60-60, е-mail: shumetov@list.ru
яковлев александр серегеевич, кандидат экон. наук
Старший преподаватель ФГБОУ ВО «Орловский государственный аграрный университет им. Н.В. Парахина», г. Орел
Тел., е-mail:
Аннотация. Рассматриваются принципы, опыт применения и перспективные возможности авторского подхода к анализу результатов анкетирования студентов многомерными статистическими методами. В основе подхода – переход от исходных переменных-признаков, измеренных в номинальных и порядковых шкалах, к вероятностям информативных вариантов ответов респондентов, оцениваемыми по их частостям. Основные положения предлагаемого подхода проиллюстрированы примерами обработки и анализа результатов анкетирования студентов Орловского государственного аграрного университета по вопросам качества обучения. Описана подготовка данных к многомерному статистическому анализу, обсуждены требования к подвыборкам, используемым для характеристики групп студентов. На примере разработки корреляционно-регрессионных и факторных моделей субъективного благополучия студентов показана эффективность предлагаемого подхода к количественному моделированию результатов анкетирования методами многомерной статистики. Показано, что для реализации технологий интеллектуального анализа данных (Data Mining) вполне достаточно располагать ранними версиями пакета статистических программ SPSS, начиная с 8-й.
Ключевые слова: анкетирование, математическое моделирование, многомерные статистические методы, исходные переменные-признаки, вероятность вариантов ответов, субъективное благополучие, корреляционно-регрессионные модели.
Поводом для обращения к проблеме многомерного статистического анализа итогов массовых опросов студентов послужили публикации последних лет, посвященные вопросам применения факторного анализа для обработки результатов анкетирования [Фомина, Жиганов, 2017; Фомина, 2017]. Факторный анализ, наряду с корреляционно-регрессионным и кластерным, является наиболее популярным из многомерных статистических методов среди исследователей-социологов: перспективы их использования в эмпирической социологии отмечались отечественными авторами еще в конце прошлого века [Татарова, 1999; Бессокирная, 2000; Черных, 2000], а в последующем корреляционно-регрессионный, факторный и кластерный анализы заняли ведущее место в учебных пособиях для студентов (см., например, [Зернов, Иудин, 2012; Терещенко, Курилович, Князева, 2012]). Считалось даже, что факторный анализ может способствовать успешному решению практически любой социологической задачи, но впоследствии из одной крайности исследователи перешли в другую крайность – почти полного отрицания его полезности для социологии [Толстова, 2007].
На наш взгляд, во многом причиной такой ситуации является специфика социологической информации: многомерные методы статистического анализа предполагают высокий уровень метризуемости пространства исходных переменных, тогда как результатам анкетирования отвечают переменные, измеренные, как правило, по номинальным и порядковым шкалам, которые, в лучшем случае, могут быть отнесены лишь к квазиинтервальным. В этой связи ряд исследователей справедливо ставят вопрос: правомерно ли использовать многомерные методы статистического анализа для исследования структуры данных, представленных в порядковой, номинальной и дихотомической шкале? Некоторые из них полагают, что включение в исследование порядковых переменных зависит от балльности шкалы, и переменные, измеренные в шкалах с пятью градациями и выше, допустимо использовать в качестве исходных данных для процедуры наиболее распространенного многомерного метода статистического анализа – факторного анализа, и чем больше выбор ответов на порядковой шкале, тем ниже вероятность серьезных ошибок при интерпретации результатов [Фомина, 2017]. Приводится и критерий применения метода: факторный анализ считается правомерным, если он используется для переменных, измеренных в порядковой шкале с большим числом градаций и имеющих согласованные матрицы корреляции, построенные с использованием коэффициента линейной корреляции Пирсона и Спирмена (или Кендалла).
Однако эти рекомендации часто не принимаются во внимание не только большинством исследователей-социологов, но даже и их авторами. Так, в публикации [Фомина, Жиганов, 2017] предлагаемая авторами методика факторного анализа для обработки результатов анкетирования проиллюстрирована на примере изучения общественного мнения на тему «Отношение тверских студентов к институту выборов». В этом примере исходными для факторного анализа выступала матрица, включающая ответы на вопросы с числом градаций от двух («да» – «нет») до максимум четырех: («да» – «скорее да» – «скорее нет» – «нет»; ответ «не знаю» вряд ли можно считать информативным). Не удивительно, что результаты факторного анализа, выполненного по методу максимального правдоподобия, оказались весьма «скудными»: авторы выделили два латентных фактора, суммарно объясняющих менее половины (точнее, 44,26%) общей дисперсии. Вряд ли социологический анализ этой факторной модели, выполненный авторами, можно считать адекватным эмпирическим данным.
Мы разделяем точку зрения А.И. Орлова [Орлов, 2012], что методы преобразования данных, которые де факто были использованы в работе [Фомина, Жиганов, 2017], допустимо использовать в разведочном статистическом анализе, цель которого – «интуитивное проникновение в закономерности массива данных» [Веллеман, Уилкинсон, 2011, 179], но в доказательной статистике такой упрощенный подход вряд ли оправдан.
Заметим, что разведочный анализ данных, как правило, осуществляется на начальных этапах обработки результатов социологических опросов, когда исследователь располагает выборками ограниченного объема. Так, в работе [Фомина, Жиганов, 2017] таблица с исходными для анализа данными была составлена по результатам анкетирования 100 респондентов, когда надежно нельзя оценить даже линейные распределения. Однако с перспективами использования социологами больших объемов данных – обращением к так называемым Big Data – появляются новые возможности технологий их обработки, включая методы Data Mining (см., например, [Мальцева, Шипкина, Махныткина, 2016]). Под термином Data Mining (англ. «добыча данных» или «раскопка данных») мы понимаем не столько принятый в социологии термин «интеллектуальный анализ данных», сколько более точный термин «извлечение знаний из баз данных» [Шуметов, Лясковская, Гудова, 2011]. В расчете на большие объемы данных, можно предложить альтернативный подход к их анализу, изложенный в работах [Гудова, Лясковская, Шуметов, 2011; Шуметов, Лясковская, 2014]. Суть подхода – в переходе от исходных переменных к переменным, измеренным в абсолютной шкале. Речь идет о вероятностях тех или иных вариантов ответов респондентов, оцениваемых по их частостям. Оценки этих вероятностей для групп респондентов, выделенных по статусным или факторным признакам, можно получить из соответствующих таблиц сопряженности.
Рассмотрим технику такого перехода на примере разработки модели удовлетворенности качеством обучения студентами Орловского государственного аграрного университета им. Н.В. Парахина (ОГАУ). Эмпирической базой моделирования служили результаты анкетирования студентов 2-4 курсов, в качестве инструментария – пакет анализа данных общественных наук SPSS Base [ SPSS Base, 2008]. Общий объем выборки составил 473 респондента, из них 166 студентов второго курса обучения, 162 и 145 – третьего и четвертого соответственно.
При формировании информативных количественных переменных существуют ограничения, вызванные ограниченным объемом выборки. Покажем это на примере построения количественной переменной, отражающей различную степень удовлетворенности выбором вуза студентами. Задача формулируется следующим образом: построить модель, отражающую влияние статусных признаков – курса обучения и пола – на степень удовлетворенности выбором вуза.
На первый взгляд, проблема решается достаточно просто: поскольку респондентам предлагается выбрать вариант степени удовлетворенности от 1 балла (низшая степень) до 5 баллов (высшая степень удовлетворенности), можно усреднить балльные оценки по шести группам студентов и построить модель, отражающую зависимость среднего балла от значений статусных признаков. При таком некорректном, однако часто используемом подходе, результирующей количественной переменной будет средний балл по вопросу «Какова степень совпадения реального образовательного процесса с Вашими ожиданиями на основе информации, представленной Университетом?».
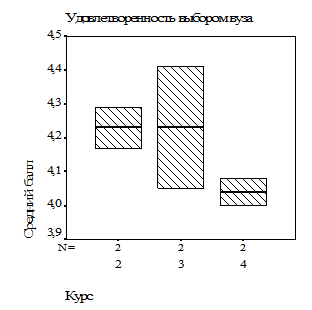
База для моделирования, полученная агрегированием исходного файла данных анкетирования по этим двум статусным признакам, приведена в таблице 1, а на рисунке 1 представлены диаграммы, иллюстрирующие распределение результирующей переменной – среднего балла – по уровням рассматриваемых признаков.
Таблица 1
Средний балл удовлетворенности выбором вуза
| Курс | Пол | |
| мужской | женский | |
| 4,29±0,785 (n =84) | 4,17±0,979 (n =82) | |
| 4,41±0,828 (n =69) | 4,05±0,982 (n =93) | |
| 4,08±1,080 (n =65) | 4,00±1,102 (n =80) |
| а | б |
| 
|
| Рисунок 1. Зависимость средней оценки удовлетворенности студентами выбором вуза: а – от курса обучения; б – от пола |
В таблице 1 данные представлены в формате «среднее±стандартное отклонение», что не является корректным. Во-первых, балльные оценки – это порядковые переменные, для которых валидной числовой характеристикой центральной тенденции являются не средние, а медианы. Если даже отнести их, как предлагают некоторые исследователи, к квазиинтервальным величинам, то и при таком допущении в рассматриваемом примере, как оказалось, распределения балльных оценок не подчиняются нормальному закону (см. рисунок 2, вариант «4 курс девушки»), следовательно, некорректным является и расчет стандартных отклонений. Тем не менее, по диаграммам рисунка 1 можно сделать вывод о тенденции снижения оценки удовлетворенности выбором вуза по мере обучения, при этом у девушек эта тенденция выражена более ярко.
| а | б |

| 
|
| Рисунок 2. Проверка на нормальность распределения балльных оценок (4 курс девушки): а – эмпирическая гистограмма; б – график «Квантиль-Квантиль» |
Таким образом, актуальным является выбор корректного и в то же время наиболее информативного показателя, отражающего степень удовлетворенности выбором вуза. Подобным показателем не может быть частость вариантов оценок «5» или «4»: опрос проводится преподавателями, и студентам проще выбрать именно эти оценки, и это приводит к систематическим ошибкам анкетирования. Оценки «2» и «1» на вопрос «Какова степень совпадения реального образовательного процесса с Вашими ожиданиями на основе информации, представленной Университетом?» выбираются студентами относительно редко, и целесообразно объединить их частости с частостями варианта оценки «3», присвоив новой переменной метку «посредственно».
В результате объединения частостей оценок по описанному алгоритму получаем базу данных для моделирования – таблица 2, а на рисунке 3 эти данные представлены в наглядной графической форме.
Таблица 2
Частость удовлетворенности выбором вуза оценкой «посредственно», %
| Курс | Пол | |
| мужской | женский | |
| 11,9 | 17,1 | |
| 11,6 | 22,6 | |
| 21,5 | 25,6 |
Из диаграмм, иллюстрирующих распределение новой, теперь уже не порядковой, а количественной переменной – частости оценки «посредственно» – по уровням статусных признаков, представленных на рисунке 3, видно, что замеченные ранее тенденции снижения удовлетворенности студентами выбором вуза с ростом курса обучения и при переходе от юношей к девушкам четко проявляют себя для медианных значений показателя.
| а | б |

| 
|
| Рисунок 3. Зависимость оценки удовлетворенности студентами выбором вуза «посредственно» от курса обучения (а) и от пола (б) |
Средний объем подвыборок по ячейкам – 15, что вполне допустимо для применения к полученной базе данных одного из эффективных методов Data Mining – процедуры обобщенной линейной модели (General Linear Model) [Бююль, Цёфель, 2002].
Не останавливаясь на деталях моделирования, приведем ее главные результаты:
1) частость оценки удовлетворенности выбора вуза «посредственно» в большей степени определяется полом и в меньшей – курсом обучения;
2) получена модель дисперсионного анализа, отражающая зависимость вероятности оценки удовлетворенности выбора вуза «посредственно» от статусных признаков «пол» и «курс обучения», которая объясняет более 90% общей дисперсии;
3) получены графики, отражающие связь вероятности оценки удовлетворенности выбора вуза «посредственно» с изучаемыми признаками (рисунок 4).
| а | б |

| 
|
| Рисунок 4. Диаграмма частости оценки выбора вуза «посредственно»для уровней статусных факторов при различных значениях другого фактора: а – пола; б – курса обучения (расчет) |
Выше рассмотрен наиболее критичный пример подготовки исходных данных анкетирования к моделированию методами дисперсионного анализа, когда выборку приходится разбивать на достаточно большое число ячеек таблицы с двумя входами. В случае разработки моделей факторного и кластерного анализа ситуация более благоприятная – группы респондентов формируются не по ячейкам двумерной таблицы сопряженности, а по градациям образующих ее признаков.
Важным фактором репрезентативности математических моделей по данным эмпирических исследований является рациональная организации анкетирования респондентов. Продуктивным здесь оказывается новаторский подход французского математика-статистика и социолога Ж.-П. Пажеса к анализу структуры факторов по результатам опросов [Пажес, 1991]. Общепринято, что адекватным методом исследования структуры факторов является факторный анализ, при этом традиционный подход заключается в представлении исходных переменных в виде
X = LF + e,(1)
где X р ´1=(X 1,..., Xр)т – матрицаисходных переменных; L р ´ m =(l ij) – матрица факторных нагрузок; F m ´1=(F 1,..., Fm)т– матрица общих (латентных) факторов; e р ´1=(e 1,..., eр)т – матрица характерных (специфических) факторов. Поскольку факторный анализ обычно проводится по выборочным данным, характеризуемым выборочной ковариационной S р ´ р =(sij) или корреляционной R р ´ р =(rij) матрицей, первой задачей факторного анализа является определение по матрице S или R оценок lij факторных нагрузок l ij и оценок специфических дисперсий.
В отличие от традиционной интерпретации модели (1), Ж.-П. Пажес предложил рассматривать факторную модель в свете «конструктивистского» подхода к механизму, приводящему к выработке мнения в результате опросов: если механизмы, которые приводят к выработке мнения, обозначить как функцию f, то ответ R (т.е. мнение) респондента и стимул S (т.е. вопрос) могут быть связаны моделью
R = f (S, P),(2)
где S и P – множества параметров, позволяющих выразить взаимодействие стимула S и индивида P. Оба эти множества указывают на два взаимосвязанные и взаимодополняющие стороны взаимодействия: коннотация (S) выражает смысл, придаваемый индивидом стимулу, а установка на дифференциацию (P) отражает умственную деятельность индивида, вызываемую стимулом [Пажес, 1991].
Чтобы оценить вид функции f, необходимо рассмотреть возмущения этой системы около заданного (во времени, пространстве, ситуации и т.п.) состояния и тем самым описать пространство состояний параметров вокруг «среднего» индивида (респондента). В первом приближении, исходя из уравнения (2), эти взаимодействия можно описать как факторную модель
X = UC + E,(3)
где X р ´ n – матрицаответов, данных n респондентами по поводу p стимулов; U р ´ k – матрица координат p стимулов в k -мерном подпространстве коннотаций; C k ´ n – матрица центрированных координат n респондентов в k -мерном подпространстве дифференциаций; Е р ´ n – матрица ошибок. Параметры коннотации и дифференциации являются неизвестными, но могут быть определены путем оптимизации, например, методом главных компонент. Но факторную матрицу U и матрицу факторных весов С можно рассматривать как репрезентативное представление всего существующего многообразия мнений и индивидов только в том случае, если в матрице данных Х с необходимой точностью воспроизведены одновременно две генеральные совокупности людей и проблем.
Рассмотрим подход Ж.-П. Пажеса на примере разработки факторной структуры субъективного благополучия студентов ОГАУ. В этом случае генеральную совокупность людей представляют студенты 2-4 курсов вуза, структурированные в различные группы, а совокупность проблем – конфликтные признаки, являющиеся компонентами субъективного благополучия студентов.
В соответствии с первым условием, выделены группы студентов, различающихся по следующим статусным и некоторым факторным признакам (в скобках указаны коды групп):
1. Факультет: агробизнеса и экологии (1); агротехники и энергообеспечения (2); биотехнологии и ветеринарной медицины (3); инженерно-строительный (4); экономический (5).
2. Направление подготовки: агроинженерия (6); агрономия (7); ветеринария (8); ландшафтная архитектура (9); строительство (10); техносферная безопасность (11); экономика (12).
3. Курс: 2-й (13); 3-й (14); 4-й (15).
4. Пол: мужской (16); женский (17).
5. Морально-нравственная атмосфера в учебной группе: «отличная» (18); «хорошая» (19); «посредственная» (20).
6. Условия, созданные в студенческой столовой: «отличные» (21); «хорошие» (22); «посредственные» (23).
7. Условия проживания в студенческом общежитии: «отличные» (24); «хорошие» (25); «посредственные» (26).
8. Организация работы университетского медпункта: «отличная» (27); «хорошая» (28); «посредственная» (29).
При выделении каждой из этих 29 групп исходили из требования их достаточной наполненности; так, из-за его нарушения в это множество не вошли такие направления подготовки, как менеджмент, биотехнология, зоотехния и некоторые другие.
В соответствии со вторым условием, в качестве конфликтных признаков, определяющих субъективное благополучие студентов, использованы полярные варианты ответов на некоторые вопросы анкеты. С учетом двух альтернативных ответов «отлично» и «посредственно» мы получаем 16 количественных переменных – частостей суждений студентов по факторам их субъективного благополучия:
1) содержание образовательных программ, методы обучения и организация учебного процесса;
2) качество преподавания дисциплин математического и естественнонаучного цикла;
3) качество преподавания дисциплин гуманитарного, социального и экономического цикла;
4) качество преподавания дисциплин профессионального цикла;
5) степень заинтересованности администрации жизнью и бытом студентов;
6) уровень признания успехов в учебной, научно-исследовательской и внеучебной деятельности;
7) степень совпадения реального образовательного процесса с ожиданиями;
8) степень уверенности в своем завтрашнем дне (возможность трудоустройства, социальная защищенность и т.д.).
Для краткости изложения результатов многомерного статистического анализа введем следующие обозначения:
- v 1- и v 1+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о качестве учебного процесса в целом;
- v 10- и v 10+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о качестве преподавания дисциплин математического и естественнонаучного цикла;
- v 11- и v 11+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о качестве преподавания дисциплин гуманитарного, социального и экономического цикла;
- v 12- и v 12+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о качестве преподавания дисциплин профессионального цикла;
- v 18- и v 18+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о заинтересованности администрации жизнью и бытом студентов;
- v 28- и v 28+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о признания успехов в учебной, научно-исследовательской и внеучебной деятельности;
- «v 58-» и «v 58+» – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос о совпадении реального образовательного процесса с ожиданиями;
- v 59- и v 59+ – частость выбора студентами вариантов ответа «посредственно» и «отлично» на вопрос об уверенности в их завтрашнем дне.
Методы многомерного статистического анализа чувствительны к нарушению нормальности распределения переменных, и по этой причине предварительно проводился «ремонт» выборки, в результате которого из исходных 29 групп студентов были исключены три группы, характеризуемые «посредственной» морально-нравственной атмосферой в учебной группе и «посредственными»условиями в столовой и общежитии. Объем выборки при этом сократился до 26 групп студентов, тогда как для корректности факторного анализа необходимо располагать двумя-тремя статистическими единицами на каждую из 16 переменных, что актуализирует предварительное сокращение размерности факторного пространства. В этих целях на начальном этапе статистических исследований выполнен множественный корреляционно-регрессионный анализ переменных v 1-, v 10-, v 11- и v 12-, с одной стороны, и переменных v 1+, v 10+, v 11+ и v 12+, с другой.
Не останавливаясь на деталях множественного регрессионного анализа, выполненного с помощью процедуры «Regression » пакета статистических программ SPSS Base 8.0 по методу «Stepwise », приведем полученные результаты.
1. Регрессионные модели оценки качества учебного процесса.
Зависимыми переменными являлись частости выбора студентами вариантов ответов на вопрос о качестве учебного процесса «посредственно» и «отлично» v 1- и v 1+ соответственно, предикторами – частости выбора студентами соответствующих вариантов ответов на вопросы о качестве преподавания дисциплин математического и естественнонаучного цикла, дисциплин гуманитарного, социального и экономического цикла, а также дисциплин профессионального цикла. В первом случае – это переменные v 10-, v 11- и v 12-, во втором – v 10+, v 11+ и v 12+.
Получены следующие линейные модели:
v 1- = 4,698 + 0,842 v 11-, (4)
v 1+ = -5,659 + 0,876 v 12+, (5)
объясняющие 89,7% и 93,2% общей дисперсии соответственно. Согласно анализу остатков, модели (4) и (5) адекватны эмпирическим данным, и это позволяет заключить, что посредственная оценка студентами качества учебного процесса определяется, в первую очередь, соответствующими оценками качества преподавания дисциплин математического и естественнонаучного цикла, а оценка «отлично» – оценками качества преподавания дисциплин профессионального цикла.
Для оценки эластичности зависимых переменных от значащих предикторов в результате применения процедуры «Regression » к логарифмически преобразованным переменным получены модели
ln v 1- = 0,946 + 0,710 ln v 11-, (6)
ln v 1+ = -0,766 + 1,125 ln v 12+, (7)
объясняющие 88,7% и 92,2% общей дисперсии соответственно. Модели (6) и (7) адекватны эмпирическим данным, что позволяет интерпретировать коэффициенты регрессии 0,710 и 1,125 как эластичность оценок учебного процесса «посредственно» и «отлично» по соответствующим оценкам качества преподавания дисциплин математического и естественнонаучного цикла, в первом случае, и качества преподавания дисциплин профессионального цикла – во втором.
2. Регрессионные модели оценки удовлетворенности выбором вуза.
Зависимыми переменными являлись частости выбора студентами вариантов ответов на вопрос о совпадении реального образовательного процесса с ожиданиями «посредственно» и «отлично» v 58- и v 58+ соответственно, предикторами – частости выбора студентами соответствующих вариантов ответов на вопрос о качестве учебного процесса в целом, а также о заинтересованности администрации жизнью и бытом студентов и признании их успехов в учебной, научно-исследовательской и внеучебной деятельности. В первом случае – это переменные v 1-, v 28- и v 18-, во втором – v 1+, v 28+ и v 18+.
Получены следующие линейные модели:
v 58- = -8,093 + 0,714 v 1- + 0,749 v 28-, (8)
v 58+ = -14,843 + 0,420 v 1+ + 0,877 v 28+, (9)
объясняющие 94,7% и 98,1% общей дисперсии соответственно. Модели (8) и (9) адекватны эмпирическим данным, и это позволяет заключить, что посредственные и отличные оценки студентами совпадения реального образовательного процесса с ожиданиями определяются соответствующими оценками качества учебного процесса в целом, а также заинтересованности администрации жизнью и бытом студентов.
Для оценки эластичности зависимых переменных от значащих предикторов в результате применения процедуры «Regression » к логарифмически преобразованным переменным получены модели
ln v 58- = -1,493 + 0,776 ln v 1- + 0,730 ln v 28-, (10)
ln v 58+ = -1,901 + 0,328 ln v 1+ + 1,150 ln v 28+, (11)
объясняющие 92,3% и 95,0% общей дисперсии соответственно. Модель (10) адекватна эмпирическим данным, что позволяет интерпретировать коэффициенты регрессии 0,776 и 0,730 как эластичности оценок совпадении реального образовательного процесса с ожиданиями «посредственно» по соответствующим оценкам качества учебного процесса в целом и заинтересованности администрации жизнью и бытом студентов. В модели (11) коэффициенты регрессии 0,328 и 1,150 интерпретируются как эластичности отличной оценки совпадении реального образовательного процесса с ожиданиями по соответствующим оценкам качества учебного процесса в целом и заинтересованности администрации жизнью и бытом студентов.
3. Регрессионные модели оценки уверенности в будущем.
Зависимыми переменными этих моделей являлись частости выбора студентами вариантов ответов на вопрос об уверенности в их завтрашнем дне «посредственно» и «отлично» v 59- и v 59+ соответственно, предикторами – частости выбора студентами соответствующих вариантов ответов на вопрос о совпадении реального образовательного процесса с ожиданиями, а также признания успехов студентов в учебной, научно-исследовательской и внеучебной деятельности и заинтересованности администрации жизнью и бытом студентов. В первом случае – это переменные v 58-, v 18- и v 28-, во втором – v 58+, v 18+ и v 28+.
Получены следующие линейные модели:
v 59- = -0,300 + 0,485 v 28- + 0,791 v 58-, (12)
v 59+ = -27,306 + 0,591 v 18+ + 0,848 v 28+, (13)
объясняющие 97,5% общей дисперсии. Модели (12) и (13) адекватны эмпирическим данным, и это позволяет заключить, что, с одной стороны, посредственные оценки студентами уверенности в их завтрашнем дне определяются также посредственными оценками заинтересованности администрации жизнью и бытом студентов и их удовлетворенности выбором вуза, с другой стороны, отличные оценки студентами уверенности в их завтрашнем дне определяются отличными оценками признания успехов студентов в учебной, научно-исследовательской и внеучебной деятельности и заинтересованности администрации жизнью и бытом студентов.
Для оценки эластичности зависимых переменных от значащих предикторов в результате применения процедуры «Regression » к логарифмически преобразованным переменным получены модели
ln v 59- = 0,110 + 0,503 ln v 28- + 0,534 ln v 58-, (14)
ln v 59+ = -3,905 + 1,019 ln v 18+ + 0,932 ln v 28+, (15)
объясняющие 96,4% и 97,2% общей дисперсии соответственно. Модель (15) адекватна эмпирическим данным, что позволяет интерпретировать коэффициенты регрессии 0,503 и 0,534 как эластичности оценок студентами уверенности в их завтрашнем дне «посредственно» по соответствующим оценкам заинтересованности администрации жизнью и бытом студентов и удовлетворенности студентов выбором вуза. В модели (15) также два предиктора, и коэффициенты регрессии 1,019 и 0,932 интерпретируются как эластичности отличной оценки студентами уверенности в их завтрашнем дне по соответствующим оценкам признания успехов в учебной, научно-исследовательской и внеучебной деятельности и по отличным оценкам заинтересованности администрации жизнью и бытом студентов.
Приведенные выше результаты выполненного регрессионного анализа, помимо их самостоятельного значения, позволяют снизить размерность исходного факторного пространства с 16 до 10 переменных и перейти к следующему этапу статистических исследований – факторному анализу по выборке после «ремонта». Не останавливаясь на деталях, приведем основные результаты факторного анализа, выполненного нами по методу главных компонент.
Главная задача первого этапа разработки модели структуры факторов субъективного благополучия студентов ОГАУ – определение оптимального числа главных факторов. В нашем случае исходные факторы сильно коррелируют, и уже два первых главных фактора объясняют почти 96% общей дисперсии, что позволяет наглядно представить структуру факторов субъективного благополучия студентов на плоскости, осями которой являются главные факторы. Другая важная задача этого этапа – оптимизация факторной структуры, что достигается путем вращения главных факторов по тому или иному критерию, чаще всего, по критерию «варимакс».
Рисунок 5 иллюстрирует две модели структуры факторов субъективного благополучия студентов ОГАУ: первую – до и вторую – после вращения пространства главных факторов. Видно, что если до вращения факторная структура практически одномерная, причем большая доля объясняемой дисперсии приходится на первый главный фактор, то вращение главных факторов по критерию «варимакс» приводит к перераспределению «нагрузок» исходных факторов на оси двумерного факторного пространства.
| а | б |

| 
|
| Рисунок 5. Структура факторов субъективного благополучия студентов ОГАУ: а – до вращения; б – после вращения главных факторов по критерию «варимакс» |
Корреляции между пятью позитивными переменными субъективного благополучия студентов v 1+, v 18+, v 28+, v 58+ и v 59+, равно и как между пятью негативными v 1-, v 18-, v 28-, v 58- и v 59-, велики, и на диаграммах рисунка 5 эти переменные трудно различить, но из таблицы 3 видно, что первый главный фактор в наибольшей мере коррелирует с переменной v 58+, второй главный фактор – с переменной v 58-. Исходя из этого, первый главный фактор можно назвать фактором удовлетворенности выбором вуза, или, иначе, фактором субъективного благополучия второй – фактором неудовлетворенности выбором вуза, или фактором субъективного неблагополучия.
Таблица 3
Корреляции исходных переменных субъективного благополучия студентов ОГАУ с главными факторами
| Код переменной | До вращения главных факторов | После вращения по критерию «варимакс» | ||
| главный фактор 1 | главный фактор 2 | главный фактор 1 | главный фактор 2 | |
| v 1- | -0,865 | 0,393 | -0,335 | 0,889 |
| v 1+ | 0,864 | 0,436 | 0,920 | -0,301 |
| v 18- | -0,878 | 0,445 | -0,308 | 0,935 |
| v 18+ | 0,898 | 0,357 | 0,888 | -0,380 |
| v 28- | -0,923 | 0,338 | -0,416 | 0,890 |
| v 28+ | 0,881 | 0,439 | 0,934 | -0,311 |
| v 58- | -0,874 | 0,465 | -0,291 | 0,947 |
| v 58+ | 0,886 | 0,444 | 0,942 | -0,311 |
| v 59- | -0,893 | 0,421 | -0,336 | 0,928 |
| v 59+ | 0,915 | 0,380 | 0,917 | -0,377 |
| Доля объясняемой дисперсии, % | 78,9 | 17,1 | 48,1 | 47,9 |
Рисунок 6 иллюстрирует связь первого и второго главных факторов с переменными v 58+ и v 58.
| а | б |

| 
|
| Рисунок 6. Корреляция с главными факторами частости выбора студентами вариантов ответа «отлично» (а) и «посредственно» (б) на вопрос о совпадении реального образовательного процесса с ожиданиями. Числа над метками – коды групп студентов |
Главные факторы 1 и 2 – абстрактные математические конструкты, и для наглядности в дальнейшем можно их заменить тесно коррелирующими с ними переменными – частостями выбора студентами полярных оценок по совпадению реального образовательного процесса с ожиданиями «отлично» (v 58+) и «посредственно» (v 58-).
Главных факторов – два, и это позволяет представить на плоскости не только распределение «нагрузок» на них исходных переменных, но и групп студентов. Для примера ниже приведены диаграммы, иллюстрирующие распределение различных групп студентов на плоскости главных факторов (рисунок 7 а) и переменных v 58+ и v 58- (рисунок 7 б), где числа над метками отвечают кодам факул