Лабораторная работа № 21
ЦЕНТРОБЕЖНАЯ СИЛА
Цель работы:
Изучение законов механики в неинерциальной системе отсчета, вращающейся относительно инерциальной. Исследование зависимости величины центробежной силы от массы тела, угловой скорости и расстояния до оси вращения.
Оборудование:
Электромотор, вращающаяся платформа с тележкой, нить, динамометр, компьютерный интерфейс Cobra3, компьютер, набор грузов.
Продолжительность работы – 4 часа.
Теоретическая часть.
1. Инерциальные системы отсчета и законы механики Ньютона
Динамикой называется раздел механики, изучающий причины возникновения механического движения. Многовековые наблюдения позволяют сделать вывод, что определяющую роль здесь играет взаимодействие тел. Его количественной характеристикой является сила:
Сила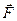 
– векторная физическая величина, мера взаимодействия тел.
Исторически сложилось так, что многочисленные эксперименты по выяснению связи между взаимодействием тел и характером механического движения проводились в системе отсчета, связанной с Землёй. В ходе этих экспериментов было установлено, что тело, не испытывающее воздействия со стороны других тел, сохраняет состояние покоя или равномерного прямолинейного движения. Однако нетрудно видеть, что в других системах отсчета это утверждение может оказаться неверным. Например, в системе отсчета, связанной с разгоняющимся автомобилем, объекты, находящиеся за окном – деревья, здания и т.п., – движутся ускоренно в сторону, противоположную направлению движения автомобиля, хотя сумма действующих на них сил остаётся равной нулю. Таким образом, прежде чем сформулировать законы динамики, необходимо дать определение систем отсчета, о которых будет идти речь в этих законах:
Первый закон Ньютона: Существуют системы отсчета, называемые инерциальными, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.
Все остальные системы отсчета называются неинерциальными.
Воздействие на данное тело со стороны других тел вызывает изменение его скорости, т.е. сообщает ему ускорение. Однако одинаковое воздействие сообщает разным телам разные ускорения, т.е. тела по-разному сопротивляются попыткам изменить их состояние движения. Это свойство тел называют инертностью.
Массой m называется скалярная физическая величина, являющаяся мерой инертности тела.
Второй закон Ньютона: Произведение массы тела на его ускорение равно действующей на него силе.
(1)
Подведём итоги:
· Законы механики Ньютона выполняются только в инерциальных системах отсчета.
· Единственной причиной ускоренного движения тела в инерциальной системе являются силы, действующие на него со стороны других тел.
· Если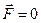 
, то согласно (1) ускорение тела также будет равно нулю. Этот вывод совпадает со второй частью формулировки первого закона Ньютона. Тем не менее, его нельзя считать следствием второго закона, поскольку главным содержанием первого закона является постулат о существовании инерциальных систем отсчёта.
2. Неинерциальные системы отсчета
Можно показать, что любая система отсчета, движущаяся прямолинейно и равномерно относительно инерциальной системы, также является инерциальной (см. например, [1], §2.7). Из этого утверждения следует, что неинерциальной системой отсчёта является любая система, движущаяся ускоренно относительно инерциальной. Простейшими неинерциальными системами отсчета являются системы, движущиеся ускоренно прямолинейно и вращающиеся системы.
Вернёмся к рассмотренному выше примеру с разгоняющимся автомобилем. Система отсчета, связанная с ним, очевидно, является неинерциальной. Второй закон Ньютона, записанный в форме (1), в данной системе отсчета не выполняется: ускоренное движение зданий и деревьев в этой системе не является результатом действия на них каких-либо сил со стороны других тел. Будем считать, что эти ускорения вызваны действием сил особой природы, называемых силами инерции. Их существование обусловлено ускоренным движением неинерциальной системы отсчета относительно инерциальной. С учетом сказанного второй закон Ньютона в неинерциальной системе отсчета примет следующий вид:
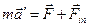(2)
где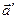 
– ускорение тела в неинерциальной системе отсчета; 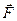– «обычные» силы, обусловленные взаимодействием тел; 
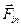– силы инерции.
Отметим главные особенности сил инерции:
· Введение сил инерции даёт возможность описывать движение тел в любых системах отсчета с помощью одних и тех же уравнений движения.
· Силы инерции обусловлены не воздействием на тело со стороны других тел, а свойствами той системы отсчёта, в которой рассматриваются механические явления. В этом смысле их можно назвать «фиктивными».
3. Центробежная сила
В данной лабораторной работе исследуются силы инерции, возникающие в неинерциальной системе отсчета, вращающейся относительно лабораторной инерциальной системы. Экспериментальная установка представляет собой платформу, вращающуюся с постоянной угловой скоростью ω вокруг перпендикулярной к ней вертикальной оси Z (см. Рис. 1, а). Вместе с платформой вращается привязанная к оси вращения небольшая тележка. Свяжем с платформой подвижную систему отсчёта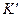 
с осями 
, как это показано на рисунке. Эта система вращается относительно лабораторной инерциальной системы K с осями X, Y, Z, а значит, является неинерциальной. Рассчитаем силу инерции, действующую на тележку в этой системе отсчета.
Тележка представляет собой твердое тело сложной формы, размерами которого в условиях данной задачи пренебречь нельзя. Поэтому сначала определим силу инерции, действующую в данной неинерциальной системе отсчета на материальную точку, а затем обобщим полученный результат для случая твёрдого тела.
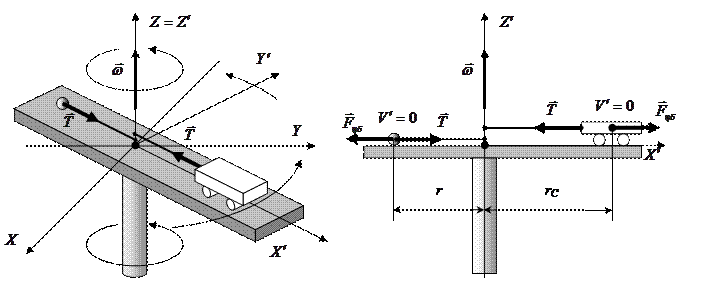
а) б)
Рис. 1 – Схематическое изображение экспериментальной установки: а) в лабораторной (инерциальной) системе отсчета; б) в неинерциальной системе отсчета, вращающейся относительно инерциальной.
1. Рассмотрим небольшой груз массы m, подобно тележке привязанный к оси вращения нерастяжимой невесомой нитью и вращающийся вместе с платформой. На Рис.1 этот груз схематически изображён слева от оси вращения. Сила тяжести скомпенсирована реакцией опоры, поэтому её в дальнейших рассуждениях рассматривать не будем. В K -системе груз движется по окружности с постоянной скоростью. Так как направление вектора скорости непрерывно изменяется, это движение является ускоренным. Ускорение направлено к оси вращения и называется центростремительным. Его величина:
(3)
где V – линейная скорость, ω – угловая скорость, а r – расстояние до оси вращения. Связанная с данным ускорением сила также называется центростремительной и по второму закону Ньютона:
(4)
В ситуации, изображённой на Рис. 1 а, в роли центростремительной силы выступает сила натяжения нити 
:
(5)
В системе отсчета 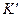(см. Рис. 1, б) груз покоится, а значит, его ускорение равно нулю. Запишем уравнение второго закона Ньютона для неинерциальных систем (2), учитывая силу инерции:
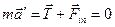(6)
Тогда для силы инерции получим:
; 
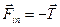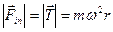(7)
Эта сила инерции называется центробежной силой. Перечислим её главные особенности:
· Центробежная сила – сила инерции, которую необходимо вводить в уравнение второго закона Ньютона при описании движения в неинерциальной системе отсчета, вращающейся с постоянной угловой скоростью относительно инерциальной.
· Вектор центробежной силы направлен от оси вращения.
· Величина центробежной силы задаётся уравнением
(8)
Пусть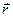 
– радиус-вектор, проведенный в неинерциальной системе отсчета к материальной точке от оси вращения. Тогда выражение для центробежной силы можно записать в векторной форме:
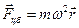(9)
2. Центробежная сила, действующая на тележку, равна сумме сил, действующих на составляющие её материальные точки:
(10)
Разделим и умножим на массу тележки m и вынесем за знак суммы одинаковый для всех точек квадрат угловой скорости. В результате получим:
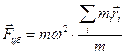(11)
Выражение
(12)
задает координаты центра масс тележки в плоскости XY. Таким образом, центробежная сила, действующая на тележку, определяется по формуле:
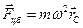(13)
А её абсолютное значение:
(14)
где rC – расстояние от оси вращения до центра масс тележки. Экспериментальной проверке этого соотношения и посвящена данная лабораторная работа.
Описание установки
Внешний вид экспериментальной установки показан на Рис. 2. Источником вращательного движения является электромотор (1) с возможностью регулировки скорости и направления вращения. Через передаточный ремень (2) вращение передаётся платформе (3) с установленной на ней тележкой (4). Для измерения расстояния от центра масс тележки до оси вращения на платформу нанесена сантиметровая шкала (5). К тележке привязана нить (6), которая через блок (7), отверстие в верхней части платформы и подвижный карабин подсоединена к динамометру (8), непрерывно измеряющему силу натяжения нити. Измеряемый сигнал через интерфейс Cobra3 (9) подаётся на персональный компьютер.
Рис. 2 – Внешний вид установки для измерения величины центробежной силы
Как описано в теоретической части, в идеальном случае сила натяжения нити должна быть равна центробежной силе. Однако в реальной экспериментальной установке выходное отверстие нити в верхней части платформы немного смещено относительно оси вращения. Это сделано намеренно: такая конструкция установки позволяет измерять не только центробежную силу, но и угловую скорость вращения. В самом деле, смещение приводит к тому, что в процессе вращения расстояние от верхнего отверстия до динамометра периодически изменяется. Вследствие этого периодически изменяется и сила натяжения нити, причём частота этого изменения совпадает с частотой вращения платформы. Таким образом, измерив зависимость силы натяжения от времени, мы сможем точно определить как частоту, так и угловую скорость вращения. В свою очередь центробежная сила будет равна среднему по времени значению силы натяжения.
Экспериментальная часть
Упражнение 1. Изучение зависимости центробежной силы от массы.
1. Установите на платформу пустую тележку без грузов. Закрепите нить на тележке таким образом, чтобы при натянутой нити центр тяжести тележки располагался на расстоянии 20 см от оси вращения. Следите за тем, чтобы нить была надета на жёлтый шкив.
2. Включите компьютер. Для входа в операционную систему используйте логин «Student ». Запустите программу Measure двойным щелчком по ярлыку на рабочем столе.
3. Согласно алгоритму, изложенному в Приложении 1, измерьте значения периода вращения и центробежной силы и занесите их в Таблицу 1 (масса пустой тележки 50 г). Определите погрешность величины 
исходя из характеристик установки и методики измерения. Погрешность измерения силы принять равной 
.
Таблица 1
| Масса тележки с грузом m, кг | Центробежная сила F, Н | Период T, с | Угловая скорость ω, рад/с |  ,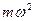
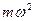кг/с2
| ∆(),
кг/с2
|
| 0,05 | … | … | … | … | … |
| 0,07 | … | … | … | … | … |
| … | … | … | … | … | … |
| 0,19 | … | … | … | … | … |
4. Постепенно нагружая тележку с шагом 20 г, повторите измерения периода вращения и центробежной силы (п.п. 6÷10).
5. Для корректного измерения зависимости центробежной силы от массы период вращения во всех измерениях должен оставаться постоянным. Однако, частота вращения в установке регулируется достаточно грубо, и поэтому период вращения в различных измерениях может немного различаться. Это необходимо учитывать. Для каждого измерения по формуле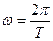 
рассчитайте угловую скорость, величину 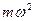и её погрешность. При этом погрешность измерения массы можно считать равной 
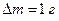. Результаты измерений занесите в Таблицу 1.
6. Постройте график зависимости центробежной силы от величины 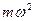. По согласованию с преподавателем построение графиков можно проводить как на миллиметровой бумаге, так и на компьютере с помощью программы Measure. Процедура построения графика с помощью компьютера подробно описана в Приложении 2.
7. Согласно формуле (14) построенная зависимость должна быть линейной. Определите угловой коэффициент прямой и сравните его с расстоянием от оси вращения до центра тяжести тележки. Сделайте вывод.