Моменты инерции прямоугольника, круга и кольца

Вопросы:

Статические моменты сечения

Моменты инерции сечения

Моменты инерции прямоугольника, круга и кольца

Изменение моментов инерции с поворотом осей. Главные оси и главные моменты инерции

Статические моменты сечения

Статическим моментом сечения относительно оси X (см. рис. 1) называется выражение:

(1)

и относительно оси Y:

(2)

Рис. 1

Статический момент имеет размерность см³ или м³, может быть положительным, отрицательным или равным нулю. Если статический момент ранен нулю, то ось проходит через центр тяжести сечения и называется центральной осью. Поэтому оси симметрии фигур вceгда являются центральными.

Определим как изменяется статический момент фигуры с параллельным переносом оси. Пусть ось Х_о является центральной (см. рис. 2), а ось X смещена на расстояние а. Из рисунка видно, что: .

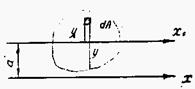
Рис. 2

Статический момент фигуры относительно оси X равен:

.

Интеграл 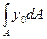представляет собой статический момент относительно оси Х_о, т.е. центральной оси. Мы уже отмечали, что статические моменты относительно центральных осей равны нулю.

;

В результате получим:

или

.

Если заменить – ординату центра тяжести фигуры, то получим:

и (2)

По формулам (2) можно определить координаты центра тяжести фигуры. Если фигура имеет сложные очертания, то ее разбивают на несколько простых (прямоугольники, треугольники, секторы, сегменты и т.д.) и статический момент находят как сумму статических моментов простых фигур. Статический момент простых фигур определяют, преобразовав формулу (2):

и (3)

Пример: Определить центр тяжести фигуры (рис. 3). Размеры даны в см.

Рис.3

Решение: Разбиваем фигуру на два прямоугольника (на рисунке пронумерованы 1 и 2). Оси X и Y проводим чeрез центр тяжести одной из фигур (прямоугольника 1), что значительно облегчает подсчеты, так как:

.

По формуле (3) находим:

,

.

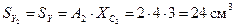Общая площадь фигуры равна:

.

Координаты центра тяжести определим по формуле (2):

;

.

Проверка: Если фигура вычерчена в масштабе, то центр тяжести находится па прямой, соединяющей центры тяжести простых фигур.

Моменты инерции сечения

Осевым моментом инерции относительно оси X называется выражение:

относительно оси Y: (4)

Полярным моментом инерции является выражение (см. рис. 4):

(5)

Осевые и полярный моменты инерции всегда положительны и имеют размерность см⁴ или м⁴. Из рисунка 4 видно, что:

поэтому:

Рис. 4

или

(6)

Полярный момент инерции равен сумме осевых.

Помимо осевых и полярного момента инерции в ряде случаев определяют центробежный момент:

. (7)

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Размерность та же, что и осевых и полярных моментов – см⁴ или м⁴.

Определим, как изменяется осевой момент инерции с параллельным переносом оси. Пусть ось Х_о – центральная (см. рис. 2). Из рисунка видно, что:

,

Тогда:

Интеграл – это момент инерции относительно центральной оси Х_о, т.е. 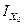интеграл 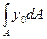– это статический момент относительно центральной оси, а он всегда равен нулю.

В результате получим:

(8)

Из формулы (8) видно, что осевой момент минимальный при а=0, т.е. центральный осевой момент имеет наименьшее значение.

Рассмотрим изменение центробежного момента инерции с параллельным переносом осей (см. рис. 5). Оси X_о и Y_о – центральные.

Рис.5

Из рисунка 5 видно, что:

, .

Центробежный момент равен:

Интеграл представляет собой центробежный момент инерции, интегралы и – статические моменты относительно центральных осей X_о и Y_о. Как известно, центральные статические моменты равны нулю. Поэтому:

(9)

Если одна из центральных осей являйся осью симметрии фигуры, то и формула (9) упростится:

(10)

Моменты инерции прямоугольника, круга и кольца