Расчет на прочность сварных соединений

Вопросы:

Понятие о сдвиге и срезе. Напряжения и деформации при сдвиге

Расчет на прочность болтовых и заклепочных соединений

Расчет на прочность сварных соединений

Понятие о сдвиге и срезе. Напряжения и деформации при сдвиге

При чистом сдвиге прямоугольный элемент, выделенный в окрестности точки и ориентированный определенным образом, испытывает только деформацию сдвига, а удлинения его сторон отсутствуют (см. рис. 1). По граням элемента действуют только касательные напряжения. Площадки, по которым действуют только касательные напряжения, называют площадками чистого сдвига. Примером тела, все точки которого испытывают чистый сдвиг, является скручиваемая труба.

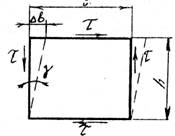
Рис.1

Величину называют абсолютным сдвигом. Она зависит oт размеров h, поэтому принято определять относительный сдвиг . Из рисунка 1 видно, что это отношение представляет собой . Для малых углов справедливо равенство . Угол называют углом сдвига, он определяет деформацию при сдвиге.

Экспериментально установлено (см. рис. 2), что до точки А деформации сдвига прямо пропорциональны касательным напряжениям, т.е. применим закон Гука:

, (1)

где G – модуль сдвига. Он характеризует жесткость материала, его способность сопротивляться угловым деформациям. Он связан с модулем продольной упругости Е следующей зависимостью:

, (2)

где – коэффициент поперечной деформации.

Рис. 2

Срез происходит, когда на стержень действуют две равные по величине, близко расположенные одна от другой и противоположно направленные силы (см. рис. 3, а).

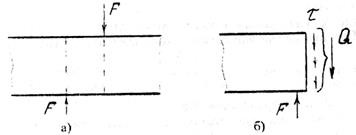
Рис. 3

Поскольку расстояние между силами очень мало, то моментом пренебрегают, и при расчете на срез учитывают одно лишь внутреннее усилие – поперечную силу Q (см. рис. 3, б), которая вызывает касательные напряжения:

;

Считается, что для каждой точки сечение одинаково, поэтому:

;

или

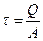(3)

Условие прочности на срез принимает вид:

, (4)

где Q – расчетная поперечная сила,

А – площадь среза,

R_s – расчетное сопротивление срезу.

Расчет на прочность заклепочного и болтового соединения

В зависимости от количества плоскостей среза заклепки или болты бывают одна, двух (см. рис. 4, а и б) – и более срезными.

Определим расчетную силу, приходящуюся на одну заклепку.

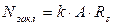(5)

где k – количество срезов заклепки (болта).

Площадь поперечного сечения заклепки (болта) равна:

,

где d – диаметр заклепки (болта).

Помимо среза при относительно тонких листах возможно нарушение соединения вследствии смятия листов или заклепки (болта) по поверхности их контакта (см. рис. 4 в и г). Фактическое распределение напряжений смятия весьма сложно и распределено по полуцилиндрам. Вычисляют условные напряжения смятия, отнесенные к площади А_{см .}, являющейся проекцией полуцилиндра на плоскость. Условие прочности на смятие:

(6)

Рис. 4

где N_закл. – усилие, приходящееся на одну заклепку (болт);

R_см. – расчетное сопротивление на смятие.

В общем случа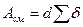е , где – наименьшая суммарная толщина листов, сминаемых в одном направлении.

Расчетная сила на заклепку (болт) равна:

Из двух значений N_закл., определенных из условия на срез и на смятие принимают меньшее. Расчет соединения состоит обычно из определения необходимого количества заклепок (болтов):

(7)

Расчет на прочность сварных соединений

Разрушение швов при соединении угловыми швами происходит от среза по наименьшей возможной площади среза, расположенной в биссектрисной плоскости угла, где наплавляется шов (рис. 5). При этом площадь среза на длине шва будет:

,

где b – коэффициент формы углового шва, зависит от вида сварки: b =0,7…1;

h_ш. – высота катета шва.

Рис. 5

Предполагая равномерное распределение касательных напряжений по площади среза, условие прочности получим в виде:

, (8)

где R_s – расчетное сопротивление сварного шва на срез.

Чтобы не допустить чрезмерной неравномерности распределения напряжений по длине шва, ставится ограничение на его длину l<60h_ш.

Задавшись высотой катета шва h_ш. можно определить расчетную длину шва по формуле:

, (9)

Фактическую длину шва принимают на 10 мм больше из-за возможности непроваривания концов шва.