Лекция №15
Тема: «Кручение»
Вопросы:
Напряжения и деформации при кручении
Главные напряжения и главные площадки при кручении
Расчет на прочность и жесткость при кручении
Напряжения и деформации при кручении
На стержень круглого сечения нанесем продольные и поперечные линии и подвергнем его скручиванию. Длина и диаметр стержня (см. рис. 1) не изменяется, не изменится и расстояние между поперечными сечениями 1-1 и 2-2. Это говорит о том, что в поперечных и продольных сечениях отсутствуют нормальные напряжения. Углы между поперечными и продольными линиями перестают быть прямыми, т.е. наблюдается угловая деформация.
Рис. 1
Угловая деформация вызывается касательными напряжениями, определяемыми по формуле:
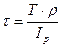(1)
где Т - крутящий момент,
- расстояние от центра сечения до рассматриваемой точки,
- полярный момент инерции.
Из формулы (1) следует, что касательные напряжения прямо пропорциональны . Для точек, одинаково удаленных от центра, касательные напряжения одинаковы по величине. При =0 (центр сечения) t=0. Максимальные касательные напряжения будут при =r.
;
Заменим 
- полярным моментом сопротивления. Тогда:
2)
Для круга:
;
;
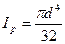(3)
Угол закручивания, т.е. угол поворота одного поперечного сечения стержня относительно другого равен:
(4)
где l - длина стержня,
- модуль сдвига.
Главные напряжения и главные площадки при кручении
При кручении в поперечных сечениях бруса возникают только касательные напряжения. Согласно закону парности касательных напряжений в продольных сечениях будут возникать равные по величине и противоположные по знаку касательные напряжения. По граням элемента будут действовать только касательные напряжения (см. рис. 2).
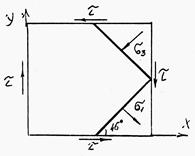
Рис. 2
Положение одной из главных площадок находят по формуле:
.
В данном случае нормальные напряжения 
, тогда:
,
.
Вторая главная площадка перпендикулярна первой.
Главные напряжения находят по формуле:
.
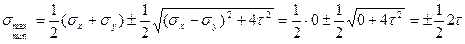Как известно: 
, поэтому:
.
При чистом сдвиге главные напряжения равны по величине и противоположны по знаку (одно растягивающее, второе сжимающее).
Характер действия напряжений при кручении подтверждается экспериментами. Чугунный образец (см. рис. 3, а) всегда разрушается под углом 45 
. Разрушающими являются напряжения 
, т.е. образец разрушается от разрыва. Напряжение 
равно по величине , но хрупкие материалы сопротивляются сжатию значительно лучше, чем растяжению, поэтому не может привести к разрушению.
Стальной образец всегда разрушается по поперечному сечению (см. рис. 3, б). Разрушение вызывают касательные напряжения в поперечном сечении. Характер разрушения – сдвиг.
Деревянный образец всегда разрушается вдоль волокон (см. рис. 3, в). Поскольку касательные напряжения в поперечном и продольном сечении равны по величине (закон парности касательных напряжений), а сопротивление дерева сдвигу вдоль волокон (скалыванию) в 5...8 раз меньше, чем на перерезание волокон, то характер разрушения закономерен.
а) б) в)
Расчет на прочность и жесткость при кручении
Теория кручения круглого бруса используется главным образом при расчете валов машин и механизмов, поэтому пользуются правилами машиностроения, т.е. расчет ведут по допускаемым напряжениям.
Условие прочности имеет вид:
где 
- допускаемое напряжение на кручение.
Значение 
определяют по формуле (2), тогда:
(5)
Из условия прочности можно решать следующие три задачи:
1. Проверить на прочность. Если расчетное сопротивление меньше или равно допускаемому, то условие прочности соблюдено. Незначительное превышение (до 5%) расчетного напряжения над допускаемым считается несущественным, и прочность тоже обеспечена. Например, =103 МПа и =100 МПа, то превышение 3% и прочность обеспечена.
2. Подобрать сечение (проектный расчет). Из формулы (5) получим:
.
Согласно формуле (3):
;
;
(6)
По формуле (6) рассчитывают диаметры валов.
3. Определить допускаемую нагрузку. Из формулы (5) получим:
, (7)
где 
- допускаемый крутящий момент. Зная его величину, можно ограничить внешнюю нагрузку.
Некоторые валы помимо расчета на прочность рассчитывают и на жесткость. Это вызвано тем, что в некоторых случаях по условиям эксплуатации приходится ограничивать величину деформации. С этой целью задается нормативный угол закручивания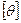 
в рад/м, т.е. угол закручивания, приходящийся на 1 м длины. Поэтому формулу (4) преобразуют, определяя относительный угол закручивания, т.е. угол, приходящийся на 1 м длины вала:
.
Условие жесткости:
или
(8)
Из условия жесткости можно решать те же задачи, что и из условия прочности.
При проектном расчете из формулы (8) получим:
,
но 
,
;
(9)
Из двух значений диаметра, определенных из расчета на прочность и жесткость принимают большее.