Глава 2
4.1. Решать можно по-разному, но для закрепления 3-го раздела полезно применить работу с матрицами.
Разберем задачу 4.1 г
Для системы 
введем матрицу коэффициентов при неизвестных 
, вектор-столбец (матрицу) неизвестных 
и вектор-столбец правых частей 
. Найдем произведение матриц 
:
. Но тогда матричное уравнение
или 
равносильно системе .
Решим полученное матричное уравнение: сначала, найдем 
, затем 
, но 
. Следовательно, 
, 
, 
.
Примечание. Т. к. я не испытывал нужды в дополнительной тренировке, матрицу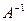 
и произведение 
я нашел при помощи пакета Mathcad.
4.4-4.5. Решим следующую НСЛАУ (неоднородную систему):
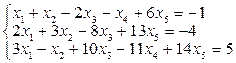
и соответствующую ей ОСЛАУ (однородную систему):
.
Начнем приводить расширенную матрицу НСЛАУ,
элементарными преобразованиями строк, сначала, к треугольному, а затем к “диагональному” виду. Получим, сначала, нули в первом столбце под первой строкой, для чего к второй строке добавим первую, умноженную на –2, а к третьей – умноженную на –3. Получим новую матрицу (расширенную матрицу системы, равносильной исходной):
.
Фактически, исключили 
из второго и третьего уравнений системы. Далее умножим вторую строку на ⅓ и новую вторую строку, для получения нуля во втором столбце ниже второй, добавим к третьей:
.
Если, теперь, вычеркнуть из матрицы нулевую строку (т.е. убрать из системы ничего не дающее уравнение 0=0), то мы получим ступенчатую (треугольную!) матрицу с двумя ненулевыми строками как во всей матрице, так и матрице, находящейся левее черты. Видно, что НСЛАУ имеет решение – ранг r матрицы коэффициентов равен рангу расширенной и равен двум. Следовательно, для получения решения надо r = 2 базисных (связанных) неизвестных, выразить через n – r = 5 – 2 = 3 оставшихся свободных неизвестных. С этой целью, начнем делать нули над диагональю (обратный ход), для чего к первой строке добавим вторую, умноженную на –1:
,
Получили в первых двух столбцах не только желаемую диагональную, но даже еще более приятную единичную матрицу, что соответствует такой системе уравнений:
.
Теперь, напрашивается выразить r = 2 базисных (связанных) неизвестных и 
через n – r = 5 – 2 = 3 свободных неизвестных 
, 
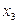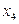и 
:
.
Для получения общего решения НСЛАУ в единообразной форме (без разделения неизвестных на две группы) введем для свободных переменных новые обозначения: 
, 
, 
. Перепишем через эти новые параметры s, t и u неизвестные и , и получим такую запись общего решения:
, 
.
Разберем, наконец, на составные части-слагаемые: первая без параметров, вторая – с первым параметром s, третья - с вторым t и т.д.:
,
и, наконец, вынесем из второго – четвертого слагаемых общие множители, что дает следующую запись общего решения НСЛАУ в векторном виде:
, .
Если взять все параметры s, t и u равными нулю, то мы получим частное решение НСЛАУ:
.
Если вернуться к однородной системе, соответствующей исходной:
,
то повторяя все действия, мы придем, сначала, также к однородной системе:
,
затем к
,
и наконец, к общему решению ОСЛАУ:
, .
Общее решение однородной СЛАУ является линейной комбинацией трех векторов 
, 
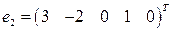и 
. Эти три вектора линейно независимы (см. 3,4 и 5 координаты) и в трехмерном линейном пространстве решений образуют базис или фундаментальную систему решений 
однородной СЛАУ.
Общее решение неоднородной СЛАУ получается состоящим из частного решения 
этой системы и общего решения однородной СЛАУ 
: 
, где , , , .
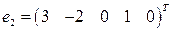Если к правой части третьего уравнения исходной неоднородной СЛАУ добавить единицу:
,
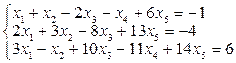то, полностью повторяя все шаги, придем к такой матрице равносильной системы:
.
У этой системы третье уравнение имеет вид 0 = 1, что означает отсутствие решения – несовместность системы. Можно заметить, что это вызвано тем, что ранг матрицы коэффициентов равен двум, а ранг расширенной матрицы – трем. Неравенство этих рангов означает разбалансировку правых частей по сравнению с левыми. Следствие – невозможность нахождения конкретного решения.
4.9. У однородной системы все правые части по определению равны нулю. Поэтому соответствующее матричное уравнение выглядит так 
и 
, если существует обратная матрица 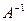. А вот если 
, то 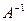не существует и у системы можно искать и ненулевые решения.
4.10. Введите текущий вектор 
в пространстве 
. Требование ортогональности будет выполнено, если скалярные произведения текущего вектора и заданных векторов приравнять нулю. Получите однородную СЛАУ, решите ее и найдите базис (см. 4.4).
4.12.а) Необходимость полного использования сырья приводит к следующей неоднородной СЛАУ из двух уравнений с тремя неизвестными:
.
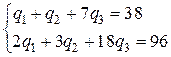Решение этой системе и введение параметра t для свободной переменной 
приводит к такому результату:
.
Условие неотрицательности величин q 1, q 2, q 3 приводит к такой системе уравнений на параметр t:
,
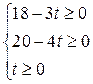откуда 
.
Выразим, теперь, стоимость продукции 
, сначала, через величины продукции q 1, q 2, q 3, а затем, через параметр t:
.
Понятно, что максимальная стоимость продукции будет при наибольшем возможном значении параметра t.