I. Взаимосвязи экономических явлений и их виды.
Различные явления, происходящие в экономике, находятся в причинно-следственной связи. Эти связи многообразны по своему характеру и различны по свей силе.
Задача статистики сводится к тому, чтобы определить эти зависимости и дать им экономическую оценку. Для этого выделяют результативный (у) и факторные (х) признаки. Признак, характеризующий следствие называется результативным. Признаки, характеризующие причину – факторными.
Виды взаимосвязей:
1. По тесноте.
А) Функциональные (полная связь).
Возникает, когда значению величины факторного признака будет соответствовать определённое значение признака результата.
Пример: Зависимость уровня оплаты труда работников (результативный признак): от объёмов выполненной работы или от времени (факторные признаки).
Б) Корреляционная связь (частичная).
Возникает, когда отдельному значению факторного признака может соответствовать несколько значений признака результата.
Пример: Зависимость урожайности сельскохозяйственных культур (результативные признак) от дозы вносимых удобрений (факторный признак). Она может проявляться, а может не проявляться, т.к. урожайность зависит и от других факторов: сроков посева, погодных условий, уровня агротехники и других – которые либо усиливают эту связь, либо нивелируют её.
2. По направлению.
А) Прямая.
Проявляется, если направление изменения факторного и результативного признаков совпадают.
Пример: Рост прибыли (факторный признак) повышает уровень рентабельности (результативный признак) и наоборот.
Б) Обратная.
Проявляется, если направления признаков не совпадают.
Пример: Рост себестоимости (факторный признак) снизит уровень рентабельности (результативный признак) и наоборот.
3. По аналитической форме.
А) Линейная.
Проявляется, если зависимость результативного признака от факторного можно выразить уравнением прямой линии:
ух = а ± bх
б) Криволинейная.
Проявляется, если зависимость результативного признака от факторного выражается уравнением кривой:
ух = а ± b / х – гипербола;
ух = а ± bх ± сх2 – парабола второго порядка.
Уравнение, с помощью которого дается оценка зависимости называется уравнением регрессии.
4. По числу факторов.
А) Парная. Возникает когда рассматривается влияние одного факторного признака на результат.
Б) Множественная. Возникает, когда рассматривается влияние двух и более факторных признаков на результат.
II. Сущность и этапы корреляционно-регрессионного анализа (КРА).
Корреляционно-регрессионный анализ дает количественную оценку наличия и направления взаимосвязей, характеризует силу и форму влияния одних факторов на другие.
Задачи регрессионного анализа: выявить наличие зависимости, установить форму связи и дать оценку абсолютной зависимости результата от фактора. Они решаются с помощью обработки массового потока информации и определения коэффициентов: регрессии и эластичности.
Задача корреляционного анализа: измерить тесноту связи между признаками. Решается с помощью определения коэффициентов: корреляции и детерминации.
Этапы корреляционно-регрессионного анализа.
1. Постановка задачи и предварительное установление причинно-следственных связей.
2. Отбор наиболее существенных признаков и сбор фактического материала.
3. Выбор показателей для оценки взаимосвязей и установление формы связи.
а) С помощью группировки данных определяется, какие показатели брать для расчета характеристик взаимосвязи.
б) С помощью построения графика зависимости определяется форма связи.
4. Расчет числовых характеристик и их экономический анализ.
А) Однофакторный корреляционно-регрессионный анализ (на примере парной корреляции линейной регрессии).
Для выявления связи между признаками строится аналитическая таблица или корреляционная матрица:
| Х У | У1 | У2 | Уz | Итого |
| Х1 | f11 | f12 | f1z | Σf1j |
| Х2 | f21 | f22 | f2z | Σf2j |
| Хk | fk1 | fk2 | fkz | Σfkj |
| Итого | Σfi1 | Σfi2 | Σfiz | Σfij = n |
fij – количество сочетаний значений х и у (частоты).
Если fij расположены в таблице беспорядочно, то связь между признаками отсутствует.
Если образуется какое-либо характерное сочетание fij – связь имеет место.
Пример: Если частоты в таблице концентрируются около одной из двух диагоналей – связь линейная.
Наглядным изображением корреляционной зависимости служит корреляционное поле (график), где на оси х откладываются значения факторного признака, оси у – результативного.
По расположению и концентрации точек судят о наличии и форме связи.
у у
 | |
….................
…..........
….. …………………..
….. …………….
… ………………………
…. х ……............. х
а) линейная связь б) связь отсутствует
В случае парной линейной зависимости строится регрессионная модель:
ух = а ± bх, где (1)
± – характеризует направление связи ((–) – обратную, (+) – прямую);
ух – значение признака результата;
х – значение признака фактора;
а – свободный член уравнения;
b – коэффициент регрессии.
Коэффициент регрессии характеризует меру абсолютной зависимости результативного признака от факторного. Он имеет те же единицы измерения, что и признак результат и показывает, как изменяется признак результат при изменении факторного признака на единицу.
Параметры уравнения регрессии (а и b) находятся методом наименьших квадратов на основе решения системы уравнений (линейного):
Σ у = аn + b х Σх
Σху = а х Σх + b х Σх2
Относительную характеристику регрессионной зависимости дает коэффициент эластичности:
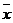
Э = b х, где (2)
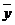
х̅ ̅ – среднее значение факторного признака;
у̅ ̅ – среднее значение результативного признака.
Этот показатель характеризует среднее изменение результативного признака (в %) при изменении факторного на 1%.
Количественная оценка тесноты связи производится с помощью коэффициента парной корреляции (в нашем случае линейной):
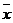– х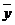
rух =, где (3)
δх х δу
δх – среднее квадратическое отклонение факторного признака;
δу – среднее квадратическое отклонение результативного признака;
– среднее значение произведения факторного и результативного признака.
Коэффициент корреляции принимает значения от –1 до 1.
Если rух = 0 – линейная связь отсутствует;
если | rух | = 1 – связь полная (функциональная);
если | rух | < 0,3 – связь слабая;
если | rух | – 0,3 … 0,7 – связь средняя;
если | rух | – 0,7 … 0,99 – связь сильная или тесная.
Для анализа относительной величины связи определяется коэффициент детерминации:
D = r2 х 100% (4)
Он показывает, сколько % вариации результативного признака обусловлено влиянием факторного.
Определение параметров корреляционно-регрессионной зависимости предполагает оценку надежности (значимости) коэффициента корреляции.
С этой целью определяют:
1) t-критерий (критерий Стьюдента):
n – 2
tкр = r х, где (5)
1 – r2
(n – 2) – число степеней свободы при заданном уровне значимости α и объёме выборки n.
2) Фактическое значение t-кр сравнивается с табличным (для α = 0,1; 0,01 или 0,05). Если фактическое значение t-кр превосходит табличное, то коэффициент корреляции значим (связь реальна).
Б) Множественный корреляционно-регрессионный анализ (на примере линейной регрессии).
При проведении этого анализа определяется перечень независимых переменных (факторных признаков), включаемых в уравнение регрессии.
Далее производится отбор наиболее значимых переменных и решается вопрос о форме уравнения (форме связи).
Уравнение линейной множественной регрессии:
ух = а ± b1х1 ± b2х2 ± … ± bnхn, где (6)
ух – значение признака результата, обусловленное влиянием нескольких признаков факторов;
х1, х2,…, хn – значения факторных признаков;
b1, b2, …, bn – коэффициенты регрессии, каждый из которых показывает на сколько единиц изменится результативный признак в связи с изменением соответствующего факторного признака на единицу при условии постоянства остальных значений х.
Для множественной регрессии определяются частные коэффициенты эластичности:
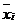
Э = bi х, где (7)
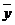
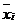– среднее значение соответствующего факторного признака;
bi – коэффициент регрессии при соответствующем факторном признаке.
Этот коэффициент характеризует, на сколько процентов изменится результативный признак при изменении факторного на 1% при фиксированном значении остальных факторов.
Для оценки тесноты связи между результативным и факторными признаками определяют коэффициент множественной корреляции (в нашем случае линейный):
δ2ост δ2
R = 1 – =, где (8)
σ2 σ2
δ2ост – остаточная дисперсия, характеризующая вариацию результативного признака за счет факторов, не включенных в уравнение множественной регрессии;
σ2 – общая дисперсия фактических данных результативного признака;
δ2 – дисперсия теоретических значений результативного признака, рассчитанная по уравнению множественной регрессии.
Этот коэффициент изменяется от – 1 до 1 и имеет туже интерпретацию, что и парный коэффициент регрессии. Чем он ближе к 1, тем связь более существенна.
Для анализа тесноты связи между факторным и результативным признаками при фиксированном значении других факторных признаков определяются частные коэффициенты корреляции.
Пример: Частный коэффициент корреляции между признаками х1 и у, при исключении влияния признака х2 определяется:
rух1 – rух2 rх1х2
rух1(х2) =, где (9)
(1 – r2ух2) (1 – r2х1х2)
r – парные коэффициенты корреляции между соответствующими признаками, определённые по формуле парного линейного коэффициента корреляции (формула 3).
Множественный коэффициент детерминации:
D = R2 х 100% (10)
Он показывает, какая часть вариации результативного признака зависит от влияния включенных в модель факторных признаков.
Для определения степени влияния одного факторного признака на результативный определяют частные коэффициенты детерминации (формула 4).
Оценка значимости коэффициента множественной корреляции осуществляется на основе F-критерия (критерия Фишера).
Фактическое значение Fкр определяется по формуле:
R2 n – m
Fкр = х, где (11)
1 – R2 m – 1
m – общее количество признаков (параметров уравнения);
n – объем выборки.
Фактическое значение Fкр сравнивается с табличным, которое находится с учетом заданного уровня значимости α (для α = 0,01 или 0,05) и числа степеней свободы k1 = m – 1 и k2 = n – m. Если фактическое значение больше фактического корреляция признаётся существенной.
III. Непараметрические методы оценки связей.
Методы оценки тесноты связи подразделяются на параметрические и непараметрические.
Параметрические методы основаны на использовании количественных характеристик признака: средних, дисперсии и других (корреляционный анализ).
Непараметрические методы позволяют измерять связь между качественными признаками.
Пример: а) зависимость между профессией и здоровьем;
б) зависимость успеваемости студентов заочников от работы их по специальности.
Непараметрические методы анализа.
1. При определении тесноты связи между двумя альтернативными признаками, представленными группами с противоположными характеристиками (хороший, плохой; успевающий, не успевающий и т.п.) определяются коэффициенты контингенции и ассоциации.
Для их расчёта используется таблица «четырех полей»:
| a | b | a + b |
| c | d | c + d |
| a + c | b + d | a + b + c + d |
a, b, c, d – частоты сочетаний пар качественных признаков.
1) Коэффициент ассоциации.
ad – bc
Ка = (12)
ad + bc
2) Коэффициент контингенции.
ad – bc
Кк = (13)
(a + b) х (b + d) х (a + c) х (c + d)
Эти коэффициенты изменяются от – 1 до 1. Чем ближе их значение к 1, тем сильнее связаны между собой изучаемые признаки. Связь считается подтвержденной, если Ка ≥ 0,5, а Кк ≥ 0,3.
2. При определении тесноты связи между качественными признаками, состоящими из более двух групп определяются коэффициенты К. Пирсона и А.А. Чупрова.
С этой целью строится таблица сопряжённости.
| Группы признака – Х | Группы признака – У | Итого | ||
| I | II | III | ||
| I | f1ух | f2ух | f3ух | nх1 |
| II | f4ух | f5ух | f6ух | nх2 |
| III | f7ух | f8ух | f9ух | nх3 |
| Итого | nу1 | nу2 | nу3 | nух |
fух – частоты сочетания признаков х и у;
nх – сумма частот строки;
nу – сумма частот столбца;
nух – сумма частот сочетаний х и у.
1) Коэффициент взаимной сопряженности К. Пирсона.
φ2
Кп =, где (14)
1 + φ2
φ2 = Σ zi – 1, где
zi – значение расчётного показателя, определённого по i-й строке.
(f1ух)2 (f2ух)2 (f3ух)2
z1 = + +: nх1;
nу1 nу2 nу3
(f4ух)2 (f5ух)2 (f6ух)2
z2 = + +: nх2;
nу1 nу2 nу3
(f7ух)2 (f8ух)2 (f9ух)2
z3 = + +: nх3.
nу1 nу2 nу3
2) Коэффициент взаимной сопряженности Чупрова.
φ2
Кп =, где (15)
(k1 – 1) (k2 – 1)
k1 – число групп по строкам;
k2 – число групп по колонкам.
Эти коэффициенты изменяются от 0 до 1. Чем они ближе к 1, тем связь теснее.
3. Метод ранговых оценок.
Заключается в ранжировании (упорядочении) объектов изучения в порядке возрастания или убывания их количественных или качественных характеристик. При этом каждому значению признака х и у присваивается соответствующий ранг. Ранг – это порядковый номер значения ранжированного признака.
По упорядоченным данным определяются показатели тесноты связи:
1) Коэффициент корреляции рангов Спирмена (английский экономист).
6 Σ di2
ρ = 1 –, где (16)
n (n2 – 1)
di2 – квадрат разности рангов значения х – Rх и значения у – Rу;
n – число наблюдений (число пар рангов).
Этот коэффициент принимает значения от 0 до ± 1. Чем он ближе к 1, тем выше связь.
2) Коэффициент корреляции рангов Кендалла.
2S
τ =, где (17)
n (n – 1)
n – число пар значений признаков х и у;
S – сумма разностей между числом последовательностей (Р) и числом инверсий (Q) по признаку У.
Расчет коэффициента выполняется в следующей последовательности:
1. Значения Х ранжируются в порядке возрастания или убывания их количественных или качественных характеристик.
2. Значения У располагаются в порядке соответствия значениям Х и ранжируются.
3. Для каждого ранга У определяется число следующих за ним рангов, превышающих его величину. Эти числа суммируются, определяя значение Р.
4. Для каждого ранга У определяется число следующих за ним рангов, меньше его величины. Суммируя эти числа, получаем значение Q.
4. Множественный коэффициент ранговой корреляции – коэффициент Конкордации.
Рассчитывается для определения тесноты связи между произвольным числом ранжированных признаков.
12 S
W =, где (18)
m2 (n3 – n)
m – число анализируемых признаков;
n – число наблюдений;
S – отклонение суммы квадратов рангов от средней квадратов рангов:
n m 2
Σ Σ Ri
n m 2 i = 1 i = 1
S = Σ Σ Ri –, где (19)
i = 1 i = 1 n
Ri – ранг i-го значения признака.