Лекция №21
Тема: Сложное сопротивление
Вопросы:
Общий метод решения задач при сложном сопротивлении.
Косой изгиб.
Внецентренное растяжение (сжатие).
Совместное действие кручения и изгиба.
Общий метод решения задач при сложном сопротивлении.
Если в поперечных сечениях бруса возникают два или более внутренних усилия, учитываемых при расчете на прочность, то это случай сложного сопротивления. Поперечный изгиб не является сложным сопротивлением, так как расчет балок в основном ведут по изгибающему моменту, а поперечная сила игнорируется.
Порядок решения задач при сложном сопротивлении следующий:
1. Методом сечений определяют внутренние усилия, строят их эпюры и находят опасные сечения. Опасным является сечение, где одно из внутренних усилий имеет максимальное значение.
2. Для опасного сечения определяют напряжения отдельно от каждого внутреннего усилия и строят эпюры. По эпюрам напряжений находят опасную точку (точки). За опасную принимается точка, где суммарные нормальные или касательные напряжения максимальны.
3. Для опасной точки составляется условие прочности. Если в опасной точке возникают только нармальные или только касательные напряжения, то суммарное напряжение сравнивается с допускаемым. Если в опасной точке возникает и касательное и нормальное напряжения, то для составления условия прочности нужно воспользоваться какой-то гипотезой прочности.
4. Перемещения определяют отдельно от каждого внутреннего усилия, а затем их слаживают с учетом направления.
Косой изгиб
Изгиб называют косым, если плоскость изгибающего момента не проходит ни через одну из главных осей сечения.
Пусть к свободному концу стержня приложена сила F, не совпадающая ни с одной из главных осей и проходящая через центр тяжести сечения (рис. 1). Если направление силы не будет проходить через центр тяжести, то помимо изгибающих моментов будет создаваться и крутящий момент. Этот случай мы рассмотрим чуть позднее.
По правилу параллелограма разложим силу F на составляющие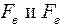 
, перпендикулярные соответственно осям X и Y. В произвольном сечении на расстоянии z от правого конца балки будут возникать изгибающие моменты:
Рис. 1
т.е. косой изгиб наблюдается, когда в сечении возникают два изгибающих момента.
Из формул (1) следует, что значения изгибающих моментов прямо пропорциональны z. При z =0; 
и при z = l 
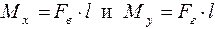. Строим эпюры моментов 
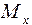и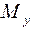 
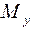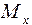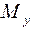. Момент действует в горизонтальной плоскости, поэтому его значения откладываем по оси X. Из эпюр и видно, что опасным будет сечение в заделке балки, так как 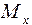и 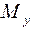максимальны.
Для опасного сечения АВСД (см. рис. 2) определим напряжения и построим их эпюры. От изгибающего момента возникают нормальные напряжения, определяемые по формулам:
От изгибающего момента 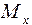напряжения будут:
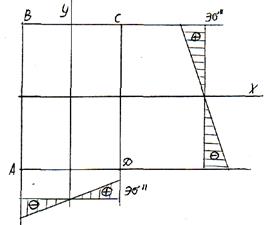
Рис. 2
от момента :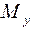
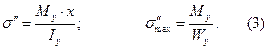
Эпюру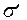 
строим справа от сечения, эпюру 
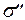– внизу. Анализируя эпюры 
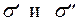видим, что наибольшие растягивающие напряжения будут возникать в точке С, а сжимающие – в точке А (опасные точки).
Условие прочности для опасной точки будет иметь вид:
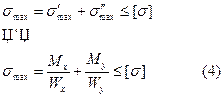
Для определения перемещений определяют отдельно прогибы от Мх и Му и затем их слаживают и определяют общий прогиб
f =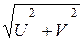 
гдеU и V - соответственно прогибы от Мy и Мx.
Внецентренное растяжение (сжатие)
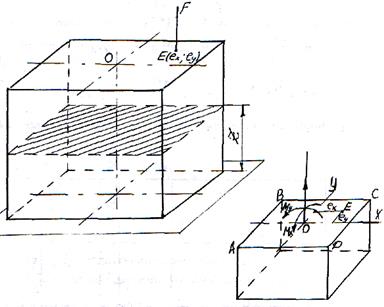
В реальных условиях часто сжимающая или растягивающая сила приложены не в центре тяжести сечения, а с каким-то смещением, например, на рисунке 3,а точка приложения силы F имеет координаты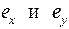 
.
а)
б)
Рис.3
Возьмем произвольное сечение на высоте z (оно заштриховано) и определим внутренние усилия. Силу F можно перенести в центр сечения, но при этом нужно добавить два момента (см. рис.3 б)
Сила F, приложенная к центру сечения вызовет продольную силу, равную ей:
N=F
Поскольку внутренние усилия не зависят от z - высоты сечения, то в любом сечении они будут одинаковы. Можно сказать, что все сечения стержня равноопасны. Определим напряжения от каждого внутреннего усилия и построим их эпюры. От продольной силы N возникают нормальные напряжения, одинаковые во всех точках сечения:
От изгибающих моментов 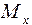и 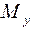соответственно:
Эпюры нормальных напряжений представлены на рисунке 6.
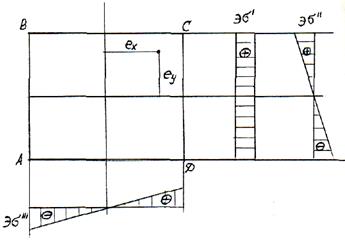
Рис. 4
Из эпюр напряжений видно, что наибольшие напряжения возникают в точке С (опасная точка). Для нее составим условие прочности:
Составим уравнение нулевой линии, т.е. линии, на которой суммарные напряжения равны нулю:
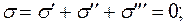
или, подставив формулы (6-8), получим:
;
Внутренние силы выразим через внешнюю силу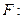 
; 
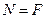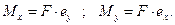Тогда получим:
;
или
;
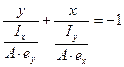Заменим
и 
, (10)
где ix,iу – радиусы инерции сечения, м.
Окончательно уравнение нулевой линии будет:
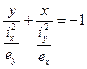; (11)
Это уравнение прямой в отрезках, так как эта прямая отсекает отрезки на осях X и Y соответственно знаменателям под переменными. Так при х=0;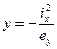 
(12) а, при у=0; 
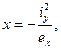(13). Поскольку в этих формулах стоит знак "минус", то у и 
, а также х и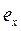 
лежат по разные стороны от центра тяжести сечения.
Все полученные зависимости справедливы и для случая внецентренного сжатия. Некоторые материалы не могут сопротивляться растягивающим усилиям. Поэтому при внецентренном сжатии нельзя допустить, чтобы какие-либо точки сечения испытывали растяжение. В этой связи важно определить зону приложения нагрузки (ядро сечения), обеспечивающую во всех точках сечения только сжатие.
Рассмотрим прямоугольное сечение. Для него согласно формуле
; 
,
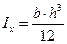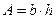где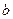 
и 
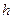– соответственно ширина и высота сечения. По формуле (10) получим:
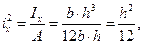(14)
Это значение 
подставим в формулу (12):
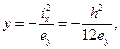(15)
Пусть нулевая линия будет проходить по самому краю сечения, т.е. линии ВС (см. рис.5, а). В этом случае в сечении будут только сжимающие напряжения, а на линии ВС напряжения будут равны нулю. При этом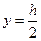 
. По формуле (15) определим 
:
Отложим эту точку на оси Y сечения.
а) б)
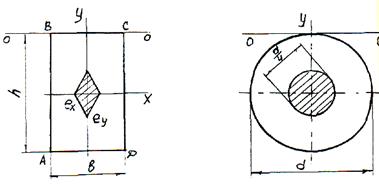
Рис. 5
Аналогично, для случая, если нулевая линия будет проходить по стороне СД прямоугольника, получим:
;
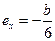Поскольку, как мы уже отмечали, для уравнения прямой в отрезках достаточно найти значения точек на осях координат, соединим эти точки.
Учитывая симметрию сечения отложим и положительные значения h/6 и b/6, что соответствует, если нулевые линии будут проходить по прямым АД и АВ.
Соединив полученные точки прямыми, определим ядро сечения (заштриховано), представляющее собой ромб.
Определим ядро сечения для круглого сечения (рис.5, б). Для круга согласно формуле:
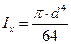и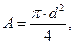 
По формуле (10):
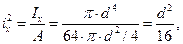
Формула (12) примет вид:
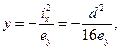
При у =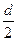 
, получим:
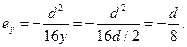
или диаметр ядра сечения будет d/4.