ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА
И ДЛИНЫСВОБОДНОГО пробега
Цель работы: исследование явления переноса – внутреннего трения (вязкости).
ПОСТАНОВКА ЭКСПЕРИМЕНТАЛЬНОЙ ЗАДАЧИ
Беспорядочное хаотическое движение молекул газа обусловливает и постоянное перемещение их масс, изменение скорости и энергии. Когда в газе имеются неоднородности плотности, температуры или скорости упорядоченного перемещения отдельных слоев газа, то за счет теплового движения молекул происходит выравнивание этих неоднородностей. При этом возникают особые процессов – явления переноса (диффузия, внутреннее трение и теплопроводность).
Явлением внутреннего трения (вязкостью) называется появление сил трения между слоями среды (газа или жидкости) движущимися друг относительно друга параллельно и с различными по модулю скоростями. Силы внутреннего трения, характеризующие взаимодействие этих слоев, направлены по касательной к поверхности соприкосновения слоев, например с площадью dS (рис.1).

За счет движения молекул происходит выравнивание скорости слоев А и В (рис.1). Это осуществляется путем переноса молекул из слоя В, движущегося со скоростью  в слой А, движущийся со скоростью
в слой А, движущийся со скоростью 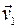 и наоборот. При этом происходит перенос импульсов
и наоборот. При этом происходит перенос импульсов  упорядоченного движения молекул. Внутреннее трение (вязкость) описывается законом Ньютона:
упорядоченного движения молекул. Внутреннее трение (вязкость) описывается законом Ньютона:
 , (1)
, (1)
где  – модуль импульса упорядоченного движения молекул перенесенный за время
– модуль импульса упорядоченного движения молекул перенесенный за время 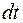 через поверхность соприкосновения слоев с площадью
через поверхность соприкосновения слоев с площадью  (рис.1);
(рис.1);  - модуль градиента скорости по нормали к слоям (изменение модуля скорости слоев на единицу длины в направлении, перпендикулярном к поверхности соприкосновения слоев); h – коэффициент внутреннего (или динамический коэффициент вязкости).
- модуль градиента скорости по нормали к слоям (изменение модуля скорости слоев на единицу длины в направлении, перпендикулярном к поверхности соприкосновения слоев); h – коэффициент внутреннего (или динамический коэффициент вязкости).
Сила трения получается по второму закону динамики
 . 2)
. 2)
Из формулы (1) вытекает физический смысл коэффициента вязкости: коэффициент внутреннего трения численно равен импульсу направленного движения молекул, переносимого за единицу времени через единицу площади соприкосновения слоев при градиенте скорости, равном единице.
Заметное отклонение молекул от прямолинейных траекторий при тепловом движении происходит только при их достаточном сближении. Такое взаимодействие между молекулами называется столкновением. Этот процесс характеризуется эффективным диаметром молекулы d, которым называется минимальное расстояние, на которое сближаются при столкновении центры двух молекул.
Путь l, который проходят молекулы между двумя последовательными столкновениями, называется длиной свободного пробега. Так как мы имеем дело с огромным числом молекул, находящихся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул  .
.
Согласно молекулярно-кинетическим представлениям
 (3)
(3)
где h – коэффициент внутреннего трения;  - средняя арифметическая скорость теплового движения молекул, равная;
- средняя арифметическая скорость теплового движения молекул, равная;
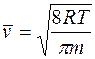 (4)
(4)
где  – молярная газовая постоянная;
– молярная газовая постоянная; 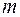 – молярная масса газа;
– молярная масса газа;  – термодинамическая температура;
– термодинамическая температура;  - средняя длина свободного пробега молекул, равная
- средняя длина свободного пробега молекул, равная
 (5)
(5)
где 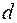 – эффективный диаметр молекул;
– эффективный диаметр молекул;  – концентрация молекул (число молекул в единичном объеме), которая при данных условиях (температуре Т и давлении Р окружающей среды) выражается формулой
– концентрация молекул (число молекул в единичном объеме), которая при данных условиях (температуре Т и давлении Р окружающей среды) выражается формулой
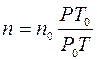 (6)
(6)
где n0 – постоянная Лошмидта – число молекул в единице объема при нормальных условиях (Р0 = 760 мм.рт.ст. = 1,013×105 Па; Т0 = 273 К).
Коэффициент внутреннего трения в данной работе определяют с помощью формулы Пуазейля для скорости течения газа по трубе:
 (7)
(7)
где  – разность давлений на концах трубки длиной
– разность давлений на концах трубки длиной 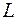 и радиусом
и радиусом  ;
;  – коэффициент внутреннего трения газа;
– коэффициент внутреннего трения газа; 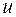 – скорость ламинарного течения газа по трубке. Этой скорости пропорционален расход газа
– скорость ламинарного течения газа по трубке. Этой скорости пропорционален расход газа  (объем газа, протекающий за 1 с через поперечное сечение трубки
(объем газа, протекающий за 1 с через поперечное сечение трубки  ).
).
 (8)
(8)
Из формул (7) (8) получаем расчетную формулу для коэффициента внутреннего трения:
 (9)
(9)
Используя формулы (1), (2) и (9), получим расчетную формулу для средней длины свободного пробега молекулы газа
 (10)
(10)
Описание установки
На рис.2 представлена блок-схема установки для определения коэффициента вязкости h воздуха. С помощью насоса 1 по капилляру 2 прогоняется воздух и давление вдоль капилляра неодинаково. Разность давлений DP на концах капилляров измеряется с помощью манометра3.
 |
Рис.2
Автотрансформатором 4 регулируется напряжение, подаваемое на насос 1, и тем самым скорость протекания воздуха через капилляр и, следовательно, расход воздуха V1 (объем воздуха, ежесекундно протекающий через поперечное сечение капилляра). Этот расход V1 указан на ручке автотрансформатора.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Включить в сеть автотрансформатор, предварительно установив его ручку на минимальный расход V1 воздуха. Это значение расхода занести в таблицу 1.
2.Снять и занести в таблицу показание манометра DPi.
3.Устанавливая ручку автотрансформатора на разные расходы воздуха V1, измерить по манометру разности давлений DPi на концах капилляра. Значения V1 и соответствующие им DPi занести в таблицу.
4.Измерить по барометру и термометру, соответственно, атмосферное давление P0 и комнатную температуру T0.
5.Используя значения V1 и соответствующие им значения DPi, провести расчеты коэффициентов вязкости воздуха hi по расчетной формуле (9).
6.Вычислить среднее арифметическое значение  .
.
7.Рассчитать среднюю длину свободного пробега молекул газа по расчетной формуле (10).
Таблица 1
P0 = …... Па; T0 =.…. 0С; Т0 =... К
Капилляр: L = 100 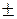 1 мм; r = 0,43 1 мм; r = 0,43 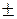 0,05 мм;
R = 8.31 Дж/(моль К); m = 2.9 10-2 кг/моль, n0 = 2.68 1025 м-3; 0,05 мм;
R = 8.31 Дж/(моль К); m = 2.9 10-2 кг/моль, n0 = 2.68 1025 м-3;
| |||||
| DPi | V1i | hi | |||
| № | кгс/см2 | Па | см3/c | м3/c | кг/(м∙с) |
КОНТРОЛЬНЫЕ ВОПРОСЫи задания
1.Какие процессы называются явлениями переноса? Перечислить эти
явления.
2.Что называется внутренним трением (вязкостью)?
3.Что за величина переносится в этом явлении переноса?
4.Написать формулу этой величины и объяснить буквенные
обозначения в ней.
5.В чем заключается физический смысл коэффициента внутреннего
трения (динамического коэффициента вязкости)? Какова связь его со средней арифметической скоростью теплового движения, средней длиной свободного пробега молекулы?
6.Что называется средней длиной свободного пробега, эффективным диаметром молекулы газа?
7.Написать формулы для средней длины свободного пробега молекулы.
8.Вывести расчетную формулу для определения коэффициента
внутреннего трения газа.
ЛИТЕРАТУРА
1.Яворский Б.М., Детлаф А.А. Справочник по физике, М. Наука, 1985.
2.Лабораторный практикум по физике. Под ред. Барсукова К.И.: М., Высш. шк., 1988.
3.Лабораторные занятия по физике. Под ред. Гольдина Л.Л., М.: Наука, 1983.