П 13. Электрохимические процессы.

Расчет количества вещества, прореагировавшего в результате электрохимической реакции, по законам Фарадея. Расчет равновесных электродных потенциалов для металлических и газовых электродов по уравнению Нернста.

Пример 1. Законы Фарадея. Расчет массы вещества, полученного в электрохимическом процессе.

Какова масса меди, выделившейся на электроде при прохождении через электрохимическую систему количества электричества, равного 2 F и выходе меди по току, равном единице (100 %)?

Решение. Количественно электрохимические превращения веществ подчиняются двум законам Фарадея:

1) масса или количество вещества, претерпевшего превращение на электроде при протекании постоянного тока, прямо пропорционально количеству прошедшего электричества;

2) при прохождении через различные электролиты одного и того же количества электричества массы различных веществ, участвующих в электродных реакциях, пропорциональны молярным массам их эквивалентов. Из этого следует, что для электрохимического превращения 1 моль эквивалента вещества требуется одинаковое количество электричества F, называемое числом Фарадея. F = 96500Кл или F =26,8 А^.час.

Оба эти закона можно объединить следующими выражениями:

расчет массы вещества: ,

где М_Э – молярнаямасса эквивалента вещества, г/моль, ;

Q – количество электричества, израсходованное на превращение вещества, Кл.

, где I – сила тока, А; t – ­ время процесса, с.

Согласно закону Фарадея при прохождении количества электричества, равного 2 F выделится 2 моль эквивалента меди, что составляет:

m _Сu= M э_Сu·2=(63,57/2)г/моль · 2 моль=63,57 г.

Пример 2. Законы Фарадея. Расчет объема газа, полученного в электрохимическом процессе. Выход по току.

Определите выход по току, выделенного на электроде при нормальных условиях водорода, если объем его составил 112 л при прохождении через электрод 1000 А·ч.

Решение. Закон Фарадея (см. Пример 1) для расчета объема газообразных веществ: ,

где V_Э – объем моль-эквивалента газа, л/моль; ;

Q – количество электричества, израсходованное на превращение вещества, Кл,

, где I – сила тока, А; t – ­ время процесса, с.

При нормальных условиях (н.у.) 1 моль любого газа занимает объем

= 22,4 л, поэтому объем 1 моля эквивалента водорода при н.у. составляет л/моль; для кислорода л/моль.

При протекании на электроде нескольких реакций на превращение каждого конкретного вещества j тратится определенная доля количества электричества В_j, называемая выходом вещества j по току, и определяемая выражением: .

Объем моль эквивалента водорода при н.у. составляет

V⁰_Э,H2 =22,4/2 = 11,2 л. Для выделения такого объема водорода требуется количество электричества, равное 1 F, или 26,8 А·ч.

Следовательно, для выделения 112 л требуется количество электричества

F ^. (V⁰_H2/V⁰_Э,H2) =26,8^.(112/ 11,2)=268 А·ч.

Найдем выход по току водорода:

B _H2 = =268 А·ч/1000 А·ч=0,27 (или 27%).

Пример 3. Расчет равновесного потенциала металлического электрода.

Вычислите равновесный потенциал никелевого электрода, если при температуре 298 К никелевая пластинка опущена в раствор соли NiSO₄ с концентрацией 0,01 моль/л.

Решение. Для металлических электродов потенциалопределяющей является реакция:

M_(р)ⁿ⁺ + n M_(тв).

Уравнение Нернста для расчета равновесного потенциала металлического электрода, поскольку активность твердой фазы принимают равной единице, имеет вид:

.

Для 298 К, переходя к десятичному логарифму, имеем:

.

Для никелевого электродов потенциалопределяющей является реакция:

Ni²⁺_(р) + 2 Ni _(тв).

Равновесный потенциал E^р _Ni²⁺_/Ni при 298 К рассчитываем по уравнению Нернста:

E^р _Ni²⁺_/Ni = E ⁰ _Ni²⁺_/Ni + (0,059/2)·lg a _Ni²⁺.

Значения стандартных потенциалов электродов в водных растворах при 298 К, определенные по водородной шкале представлены в Приложении 6 [1]. E ⁰ _Ni²⁺_/Ni = -0,25 В.

Активность ионов Ni²⁺ находим по формуле:

а _Ni²⁺ =γ_Ni²⁺· c _Ni²⁺, где γ_Ni²⁺ - коэффициент активности, который определяется ионной силой раствора I:

I =0,5(c _Ni²⁺· z ² _Ni²⁺ + c _so4^2- · z ² _so4^2- )=0,5(0,01·2²+0,01·(-2)²)=0,04.

Коэффициент активности при данном значении ионной силы равен γ_Ni²⁺=0,895. Следовательно, а _Ni²⁺=0,895·0,01моль/л=8,95·10^-3моль/л.

После подстановки значений стандартного потенциала E ⁰ _Ni²⁺_/Ni и активности а _Ni²⁺ в уравнение для расчета потенциала получаем:

E^р _Ni²⁺_/Ni = -0,25 + (0,059/2)·lg 8,95 ·10^-3=-0,31 B.

Пример 4. Расчет равновесного потенциала водородного электрода.

Рассчитайте значение равновесного потенциала водородного электрода при =5·10^-7, pH=2, T =298 К.

Решение. Для водородного электрода потенциалопределяющая реакция

2Н⁺ + 2 Н₂,

уравнение Нернста запишем в виде:

.

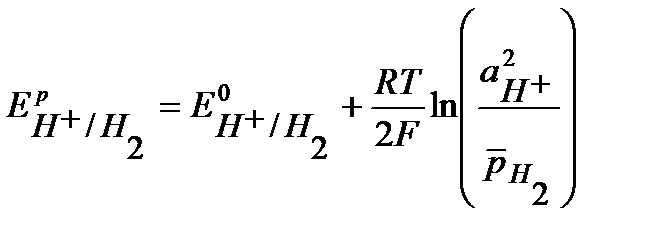Поскольку стандартный потенциал , (см. Приложение 6[1]), а водородный показатель , то при 298 К имеем выражение для расчета равновесного водородного потенциала:

.

Равновесный потенциал водородного электрода находим по этому выражению уравнения Нернста:

E^р _H+/H2 = -0,0295· lg –0,059pH= -0,0295·lg 5·10^-7-0,059·2= -0,068 В.

Пример 5. Расчет равновесного потенциала кислородного электрода.

Рассчитайте значение равновесного потенциала кислородного электрода при =5, pH=2, T =298 К.

Решение. Газовый кислородный электрод представляет собой Pt – электрод, на котором осуществляется потенциалопределяющая реакция:

О₂ + 4 + 2Н₂О 4ОН^- .

Уравнение Нернста для такого электрода:

.

Стандартный потенциал кислородного электрода = 0,401В (при и моль/л) по водородной шкале (Приложение 6 [1]). При 298 К, учитывая что 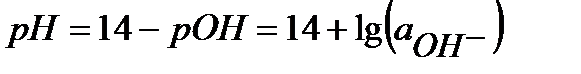, имеем удобное выражение для расчета потенциала кислородного электрода:

.

Воспользуемся этим выражением уравнения Нернста для расчета равновесного потенциала кислородного электрода:

E^р _О2/ОH- =1,23 +0,0147· lg –0,059pH =1,23+0,0147· lg 5–0,059^.2=1,12 В.