МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Методические указания
К выполнению расчетной работы по курсу
«Основы компьютерного проектирования и моделирования РЭС»
Тема: «Анализ зависимостей погрешностей моделирования от метода синтеза модели, точности представления чисел, шага дискретизации»
Утверждено
на заседании кафедры
Протокол № _____________________
Зав. кафедрой № 407
_______________________
(Меркишин Г.В.)
МАИ (ГТУ), 2010
Анализ зависимостей погрешностей моделирования от метода синтеза модели, точности представления чисел, шага дискретизации
Задание 1.1. 1) Разработать цифровые модели инерционного RC-звена в виде рекурсивных фильтров двумя различными методами. Исходные данные на моделирование заданы в табл.1.1.
2) Исследовать зависимость ошибки вычисления реакции модели на заданное входное воздействие от шага дискретизации 
. При исследовании должна быть определена область значений , где ошибка минимальна. Способ вычисления ошибки выбрать.
Табл.1.1.
| Номер варианта | ||||||
| R, Ом | 104 | 103 | 105 | 105 | 103 | 103 |
| C, Ф | 10-6 | 10-6 | 10-6 | 10-6 | 10-12 | 10-12 |
| i | ||||||
 , с
| 10-2 | 10-3 | 10-1 | 10-1 | 10-9 | 10-9 |
| 
| 
|
| 
|
|
|
Задание 1.2. 1) Разработать цифровые модели форсирующего звена (дифференцирующая RC-цепь) в виде рекурсивных фильтров двумя различными методами. Исходные данные на моделирование заданы в табл.1.2.
2) Исследовать зависимость ошибки вычисления реакции модели на заданное входное воздействие от шага дискретизации . При исследовании должна быть определена область значений , где ошибка минимальна. Способ вычисления ошибки выбрать.
|
|
Табл.1.2
| Номер варианта | |||||
| R, Ом | 5×103 | 5×103 | 5×103 | 5×103 | 5×103 |
| C, Ф | 5×10-6 | 5×10-6 | 5×10-6 | 5×10-6 | 5×10-6 |
| i | |||||
| , c
| 25×10-3 | 25×10-3 | 25×10-3 | 25×10-3 | 25×10-3 |
|
| 
|
|
|
|
|
| Методы | II, III | II, III | II, III | II, IV | II, IV |
Задание 1.3. 1) Разработать цифровые модели инерционного RC-звена в виде рекурсивных фильтров двумя различными методами. Исходные данные на моделирование заданы в табл.1.3.
2) Исследовать зависимость ошибки вычисления реакции модели на заданное входное воздействие от числа значащих цифр при округлении коэффициентов рекурсивных фильтров. Способ вычисления ошибки выбрать.
Табл.1.4.
| Номер варианта | |||||
| R, Ом | 104 | 104 | 104 | 104 | 104 |
| C, Ф | 10-6 | 10-6 | 10-6 | 10-6 | 10-6 |
| i | 1¸6 | 1¸6 | 1¸6 | 1¸6 | 1¸6 |
| , c
| 5×10-2 | 5×10-2 | 5×10-2 | 5×10-2 | 5×10-2 |
|
|
|
|
|
|
|
| Методы | I, III | I, III | I, III | II, IV | II, IV |
| Т, с | 0,2×10-2 | 0,2×10-2 | 0,2×10-2 | 0,2×10-2 | 0,2×10-2 |
Задание 1.4. 1) Разработать цифровые модели форсирующего звена (дифференцирующей RC-цепи) в виде рекурсивных фильтров двумя различными методами. Исходные данные на моделирование заданы в табл.1.4.
2) Исследовать зависимость ошибки вычисления реакции модели на заданное входное воздействие от числа значащих цифр при округлении коэффициентов рекурсивных фильтров. Способ вычисления ошибки выбрать.
Табл.1.4.
| Номер варианта | ||||||
| R, Ом | 103 | 104 | 105 | 103 | 104 | 105 |
| C, Ф | 10-6 | 10-6 | 10-6 | 10-9 | 10-9 | 10-9 |
| , c
| 5×10-3 | 5×10-2 | 5×10-1 | 5×10-6 | 5×10-5 | 5×10-4 |
| i | 1¸6 | 1¸6 | 1¸6 | 1¸6 | 1¸6 | 1¸6 |
|
|
|
|
|
|
|
|
| Т, с | 0,2×10-3 | 0,2×10-2 | 0,2×10-1 | 0,2×10-6 | 0,2×10-5 | 0,2×10-4 |
|
|
В таблицах приняты следующие обозначения:
I - метод инвариантности импульсной характеристики;
II - метод инвариантности переходной характеристики;
III – метод билинейного z-преобразования;
IV - метод согласованного z-преобразования.
- входное воздействие:
- d - функция;
- единичный скачок;
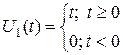
Методические указания к выполнению
Пример.
1. Разработать цифровые модели в виде рекурсивных фильтров цепи двумя самостоятельно выбранными методами. Исследовать зависимость ошибки при моделировании от точности задания коэффициентов (1,2,…,6 значащих цифр).
 |
Исходные данные: 1) шаг дискретизации 
; 2) входной сигнал - - единичный скачок; 3) интервал моделирования 
с; 4) критерий оценки ошибки моделирования – выбирается.
Используемый математический аппарат: передаточная функция моделируемого звена 
; полюс передаточной функции 
; ноль передаточной функции 
; число нулей передаточной функции 
; число полюсов передаточной функции 
. При 
метод инвариантности импульсной характеристики использовать нельзя. Построим модели по методам согласованного и билинейного z-преобразований.
Применение метода согласованного z-преобразования приводит к передаточной функции модели
.
В соответствии с заданием передаточная функция модели
,
; 
; 
.
Применяя метод билинейного z-преобразования, получим для передаточной функции модели
.
Числовые значения коэффициентов передаточной функции в этом случае равны:
; 
; 
.
Таким образом, при моделировании числовые значения коэффициентов цифровых рекурсивных фильтров в зависимости от числа значащих цифр 
будут принимать следующие значения.
|
|
Метод согласованного z-преобразования.
; 
; 
;
; ; 
;
; ; 
;
; ; 
;
; ; 
;
; ; 
.
Метод билинейного z-преобразования.
; 
; ;
; 
; ;
; 
; ;
; 
; ;
; 
; 
;
; 
; 
.
При 
округление коэффициентов не производилось, так как значение 
приводит к неустойчивости модели. Точность модели будем оценивать по среднеквадратическому отклонению результата моделирования от известной реакции заданной цепи на входное воздействие в виде единичного скачка. Таким образом, ошибка моделирования
,
где 
; 
- величина интервала моделирования в дискретах.
Результаты моделирования. Часть результатов моделирования представлена графически на рис. 2.
Зависимость ошибки моделирования 
от числа значащих цифр приведена в таблице 1 и на рис.3.
Таблица 1
| i | s | |
| Согласованное z-преобразование | Билинейное z-преобразование | |
| 2,2×10-1 | 2,6×10-1 | |
| 7,4×10-3 | 2,6×10-2 | |
| 1,4×10-3 | 1,8×10-2 | |
| 5,3×10-4 | 1,6×10-2 | |
| 4,5×10-4 | 1,6×10-2 | |
| 4,0×10-4 | 1,6×10-2 |
Анализ результатов моделирования показывает, что применение метода билинейного z-преобразования в рассматриваемом случае менее эффективно, чем метода согласованного z-преобразования, так как первый имеет существенно большую (на порядок и выше) ошибку. Характер зависимости от числа значащих цифр показывает, что метод билинейного z-преобразования имеет весьма большую алгоритмическую погрешность. Для значений 
ошибка моделирования практически не зависит от числа значащих цифр, т.е. определяется только алгоритмической погрешностью, равной примерно 
. Метод согласованного z-преобразования для рассматриваемого случая имеет алгоритмическую погрешность существенно меньшую, и определяется в основном лишь вычислительной ошибкой. (Можно показать, что алгоритмическая погрешность в данном случае равна нулю).
2. Разработать две цифровые модели в виде рекурсивных фильтров для инерционного звена рис.4 по методам инвариантности импульсной характеристики и билинейного z-преобразования. Исследовать зависимость ошибки при моделировании от шага дискретизации Т для двух моделей. Точность задания коэффициентов – две значащие цифры без округления.
 |
Исходные данные: 1) входной сигнал - - единичный скачок; 2) интервал моделирования с; 3) критерий оценки ошибки моделирования – выбирается.
Используемый математический аппарат: передаточная функция моделируемого звена 
; 
. Полюс передаточной функции .
Передаточная функция модели определяется в виде 
при
; 
; 
.
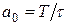При определении передаточной функции модели по методу билинейного z-преобразования получим
; 
.
Результаты моделирования. Выберем в качестве критерия отличия выходных сигналов модели и устройства среднее квадратическое отклонение
,
где 
- переходная характеристика инерционного звена (реакция на заданное входное воздействие); 
- выходной сигнал модели; 
- число отсчетов реакции на заданном интервале моделирования ; 
; 
- целая часть от x.
Результаты моделирования представлены в таблице 2 и 3 и рис.5.
Таблица 2 
| Т, мс | 
| 
|
|
| 0,36 | 8,7×10-1 | ||
| 0,1 | 0,1 | 0,90 | 7,7×10-2 |
| 0,01 | 0,01 | 0,99 | 7,8×10-3 |
| 0,0075 | 0,0075 | 0,99 | 3,7×10-2 |
| 0,005 | 0,005 | 0,99 | 1,0×10-1 |
| 0,0025 | 0,0025 | 0,99 | 2,2×10-1 |
| 0,0001 | 0,0001 | 0,99 | 3,2×10-1 |
В таблице 2 приведены результаты моделирования по методу инвариантности импульсной характеристики, в таблице 3 – по методу билинейного z-преобразования. Приближенные значения 
обозначены 
.
Анализ результатов моделирования показывает, что минимальное значение ошибки соответствует 
с.
Таблица 3 
| Т, мс |
|
|
|
| 3,3×10-1 | 3,3×10-1 | 2,5×10-1 | |
| 0,1 | 4,7×10-2 | 9,0×10-1 | 2,5×10-2 |
| 0,01 | 4,9×10-3 | 9,9×10-1 | 5,0×10-3 |
| 0,0075 | 9,7×10-3 | 9,9×10-1 | 4,3×10-2 |
| 0,005 | 2,4×10-3 | 9,9×10-1 | 1,2×10-1 |
| 0,0025 | 1,2×10-3 | 9,9×10-1 | 2,2×10-1 |
| 0,0001 | 4,9×10-4 | 9,9×10-1 | 3,2×10-1 |
 |
При 
наблюдается рост значения из-за увеличения алгоритмической ошибки. Алгоритмическая ошибка при использовании метода билинейного z-преобразования в рассматриваемом случае меньше, чем при методе инвариантности импульсной характеристики. При 
рост определяется вычислительной ошибкой, причем вычислительные ошибки для обоих методов приближенно равны.